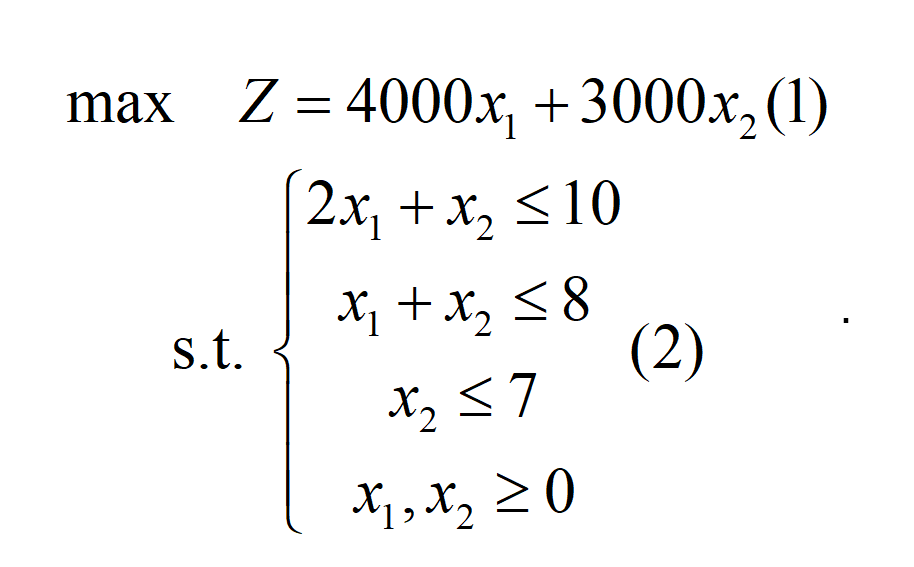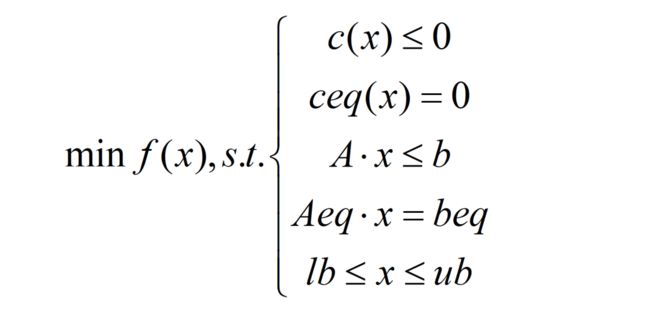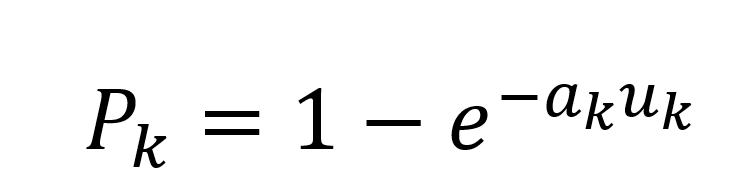MATLAB数学建模-规划模型总结| MATLAB求解

目录

1 线性规划问题（LP）

风格1

风格2

2 非线性规划

3 动态规划

A星算法

基于dijkstra的概率路线图

4 多目标规划

帕累托最优

支配（Dominace）

不可支配解集

帕累托最优解集

帕累托最优前沿面

线性加权法

约束转化法

多目标遗传算法

---

本文总结数学建模中常用的数学规划模型，并附详细的MATLAB求解案例。分为四个模块：

求解数学模型的一般步骤如下：

•读题+理解模型；

•设计  决策变量；

•列出  目标函数及约束条件；

•表示（画）出约束条件代表的可行域;

•在可行域内求目标函数的最优解及最优值;

如果你还不太理解，跟着例子往下看...

1 线性规划问题（LP）

求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。

举一个简单案例：

例：某机床厂生产甲、乙两种机床，每台销售后的利润分别为4000元与3000元。生产甲机床需用A、B机器加工，加工时间分别为每台2小时和1小时；生产乙机床需用A、B、C三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？

根据上述描述建立数学模型：

设该厂生产x1台甲机床和x2乙机床时总利润最大，则x1,x2应满足:

上式中：

•   x1 , x2 称之为决策变量;

•（1）式被称为问题的目标函数;

•（2）中的几个不等式是问题的约束条件，记为 s.t.(即 subject to);

上面的目标函数及约束条件均为线性函数，故被称为线性规划问题。

在解决实际问题时，把问题归结成一个线性规划数学模型非常重要，但往往也最困难，模型建立得是否恰当，直接影响到求解。选适当的决策变量，是建立有效模型的关键之一。

线性规划的目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便，MATLAB中规定线性规划的标准形式为:

其中c 和 x 为 n 维列向量， A 、 Aeq 为适当维数的矩阵，b 、beq 为适当维数的列向量；lb与ub分别为x的下界和上界，维度与x对应。

模型已经表示为MATLAB的标准形式，下面就可以采用MATLAB进行求解了，此处采用linprog函数。

风格1

function lp_% MATLAB求解线性规划问题，linprog% c = -[4000;3000]; % 目标函数系数A = [2 1;1 1;0 1]; b = [10;8;7];Aeq = [];beq = [];lb = [0 0]; % 变量下界x = linprog(c,A,b,Aeq,beq,lb)fval = -c'*x

需要注意的就是将约束条件转换为合适维度的矩阵！

如果你不太想进行矩阵（系数）转换，也可以采用另一种编程风格：

风格2

% 返回的fval是负的，% 即使问题是正的，% 在matlab内部，prob2struct将最大化问题转化为目标函数负的最小化问题x1 = optimvar('x1','LowerBound',0,'UpperBound',inf);x2 = optimvar('x2','LowerBound',0,'UpperBound',7);prob = optimproblem('Objective',4000*x1 + 3000*x2,'ObjectiveSense','max');prob.Constraints.c1 = 2*x1 + x2 <= 10;prob.Constraints.c2 = x1 + x2 <= 8;problem = prob2struct(prob);[sol,fval,~,output] = linprog(problem)

相信通过上述的简单例子，你已经对线性问题的建模和求解有了一定的了解，下面我们看更复杂的模型。

2 非线性规划

若目标函数·或·约束条件中包含非线性函数，就称这种规划问题为非线性规划问题。

非线性规划问题有无约束和有约束两种，它们的求解思路不太一致，具体的方法可以参考“运筹学”或者“最优化”的书籍；其中一类比较特殊的问题是二次规划问题。

一般说来，解非线性规划要比解线性规划问题困难得多。而且，也不像线性规划有单纯形法这一通用方法，非线性规划目前还没有适于各种问题的一般算法，各方法都有特定的适用范围。

线性规划与非线性规划的区别在于：如果线性规划的最优解存在，则其最优解只能在其可行域的边界上达到（特别是可行域的顶点上达到），而非线性规划的最优解（如果存在）可能在其可行域的任意一点达到。下方线性问题的图解法很容易反映解在顶点这一性质：

图解法

非线性规划问题在MATLAB里的标准形式为：

在非线性求解时常用的函数为fmincon，举一个示例模型来看看它的用法:

下方为fmincon的调用格式：

不包含非线性约束[X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = fmincon(FUN,X0,A,B,Aeq,Beq,LB,UB) 

包含非线性约束[X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = fmincon(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON) 

自己定义目标函数和非线性约束[X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = fmincon(@(X)MYOBJ(X),X0,A,B,Aeq,Beq,LB,UB,@(X)MYCON(X))性约束函数% 目标函数function F = MYOBJ(X)F = ......% 非线性约束函数function [G,Heq] = MYCON(X)G = ..... % 非线性不等式约束条件,G<=0Heq = ..... % 非线性等式约束条件,Heq == 0

（该模型的代码在文末下载）

采用fmicon的求解结果为：

除了采用默认的内点法外，也可以根据需要为fmincon函数设置不同的寻优算法：

接下来是动态规划问题。

3 动态规划

动态规划基本思路

•将多阶段决策过程划分阶段，恰当地选择状态变量、决策变量以定义最优指标函数，从而把问题化成一族同类型的子问题，然后逐个求解；

•求解时从边界条件开始，逆序过程行进，逐段递推寻优．在每一个子问题求解时，都要使用它前面已求出的子问题的最优结果．最后一个子问题的最优解，就是整个问题的最优解；

•动态规划方法是既将当前一段与未来各段分开，又把当前效益和未来效益结合起来考虑的一种最优化方法，因此每段的最优决策选取是从全局考虑的，与该段的最优选择一般是不同的；

学习动态规划，我们首先要了解多阶段决策问题。 比如：

生产决策问题：企业在生产过程中，由于需求是随时间变化的，因此企业为了获得全年的最佳生产效益，就要在整个生产过程中逐月或逐季度地根据库存和需求决定生产计划。

机器负荷分配问题：某种机器可以在高低两种不同的负荷下进行生产。要求制定一个五年计划，在每年开始时，决定如何重新分配完好的机器在两种不同的负荷下生产的数量，使在五年内产品的总产量达到最高。

航天飞机飞行控制问题：由于航天飞机的运动的环境是不断变化的，因此就要根据航天飞机飞行在不同环境中的情况，不断地决定航天飞机的飞行方向和速度（状态），使之能最省燃料和完成飞行任务（如软着陆）。

　　针对多阶段决策过程的最优化问题，美国数学家Bellman等人在20世纪50年代初提出了著名的最优化原理，把多阶段决策问题转化为一系列单阶段最优化问题，从而逐个求解，创立了解决这类过程优化问题的新方法：动态规划。对最佳路径（最佳决策过程）所经过的各个阶段，其中每个阶段始点到全过程终点的路径，必定是该阶段始点到全过程终点的一切可能路径中的最佳路径（最优决策），这就是Bellman提出的著名的最优化原理。即：一个最优策略的子策略必然也是最优的。

我们还是直接看一个求解案例:

例：设有m=4个目标，目标价值（重要性和危害性）各不相同，用数值Ak（k=1，2，…,m)表示，计划用n=5枚导弹突袭，导弹击毁目标地概率

中a_k是常数，取决于导弹地特性与目标地性质；u_k为向目标发射地导弹数，如何做出方案使预期地突击效果最大？

首先需要建立问题的模型：

根据模型和动态规划算法建立函数文件：

主函数clear n = 5;x1 = [n;nan*ones(n,1)];x2 = [0:n]';x = [x1 x2 x2 x2][p f] = dynprog(x,'DecisF1','SubObjF1','TransF1','ObjF1')disp('p的第三列是决策变量值')

决策函数function u = DecisF1(k,x)% 决策函数if k ==4    u =x;else    u = 0:x;endend

状态转移方程function y = TransF1(k,x,u)% 状态转移方程y = x-u;end

阶段k的指标函数function v = SubObjF1(k,x,u)% 阶段k的指标函数a = [0.2 0.3 0.5 0.9];A = [8 7 6 3];v = A(k)*(1-exp(-a(k)*u));v = -v;end

基本方程中的函数function y = ObjF1(v,f)% 基本方程中的函数y = v+f;% y = -y;end

动态规划dynprog函数function [p_opt, fval] = dynprog(x,DecisFun, SubObjFun, TransFun, ObjFun)% 动态规划逆序算法% x是状态变量，一列代表一个阶段状态；% DecisFun(k,x)由阶段k的状态变量x求出相应的允许决策变量；% SubObjFun(k,x,u)是阶段指标函数;% TransFun(k,x,u)是状态转移函数，其中x是阶段k的某状态变量，u是相应的决策变量；% ObjFun(v,f)是第k阶段至最后阶段指标函数，当ObjFun(v,f) = v+f时，输入的ObjFun可以省略；% fval是一个列向量，各元素分别表示p_opt各最优策略组对应始端状态x的最优函数值

在动态规划问题中，路径规划也非常重要，下方列出了关于A星算法和概率路线图（基于dijkstra算法）的求解案例:

A星算法

function path=AStar(obstacle,map)path=[];        %用于存储路径open=[];        %OpenList,考虑的节点close=[];       %CloseList，不考虑的节点findFlag=false; %findFlag用于判断while循环是否结束%% 1.将起始点放在Openlist中% open：[节点坐标，代价值F=G+H,代价值G,父节点坐标]open =[map.start(1), map.start(2) ,...    0+h(map.start,map.goal) ,...    0 , ...    map.start(1) , map.start(2)];%与当前节点的坐标差值（前两列）%与当前节点的距离值（最后一列）NEXT = [-1,1,14;...    0,1,10;...    1,1,14;...    -1,0,10;...    1,0,10;...    -1,-1,14;...    0,-1,10;...    1,-1,14];%% 2. 循环以下过程while ~findFlag         %--------------------首先判断是否达到目标点，或无路径-----    if isempty(open(:,1))        disp('没有目标路径');        return;    end        %判断目标点是否出现在open列表中    [isopenFlag,Id]=isopen(map.goal,open);    if isopenFlag        disp('找到目标');        close = [open(Id,:);close];        findFlag=true;        break;    end            %按照Openlist中的第三列（代价函数F）进行排序，查找F值最小的节点    [Y,I] = sort(open(:,3)); %对OpenList中第三列排序    open=open(I,:);%open中第一行节点是F值最小的        %将F值最小的节点(即open中第一行节点)，放到close第一行(close是不断积压的)，作为当前节点    close = [open(1,:);close];    current = open(1,:);    open(1,:)=[];%因为已经从open中移除了，所以第一列需要为空        %对当前节点周围的8个相邻节点进行计算，算法的主体：------------------------    for in=1:length(NEXT(:,1))                        m=[current(1,1)+NEXT(in,1) , current(1,2)+NEXT(in,2) , 0 , 0 , 0 ,0];        m(4)=current(1,4)+NEXT(in,3); % m(4)  相邻节点G值        m(3)=m(4)+h(m(1:2),map.goal);% m(3)  相邻节点F值                        if isObstacle(m,obstacle)            continue;        end        [flag,targetInd]=findIndex(m,open,close);        if flag==1            continue;        elseif flag==2            m(5:6)=[current(1,1),current(1,2)];            open = [open;m];        else            if m(3) < open(targetInd,3)                m(5:6)=[current(1,1),current(1,2)];                open(targetInd,:) = m;            end        end    end        %绘制    pause(0.01);    fillPlot(close,[204,159,42]/255);    hold on;    fillPlot(open,[51,102,153]/255);    end%% 3. 追溯路径path=GetPath(close,map.start);end

基于dijkstra的概率路线图

% 载入地图% --------------------------------------------------------—————————% PIC = imread(uigetfile('*.png'));         % 载入地图PIC = imread('map2.png');                    % 载入地图imshow(PIC);                                % 显示地图hold on;% 关键参数% --------------------------------------------------------—————————feasibleR = 51;                             % 可行区域的红色值【0~255】NUM = 200;                                  % 离散点规模% 一些样式设置，可以注释掉% --------------------------------------------------------—————————ax = gca;ax.Parent.Units = 'normalized';ax.Parent.Color = 'k';ax.Parent.Position = [0.1 0.1 0.8 0.7];ax.Units = 'normalized';ax.Position = [0.1 0.001 0.8 0.998];ax.Color = [51 51 51]/255;% 选择起/始点% --------------------------------------------------------—————————StartPoint = ginput(1);EndPoint = ginput(1);                       scatter([StartPoint(1) EndPoint(1)],[StartPoint(2) EndPoint(2)],...    'filled','SizeData',150,'MarkerFaceColor',[199 237 53]/255,'MarkerEdgeColor','w');% 绘制出起始点pause(1)% 生成并绘制可行点%__________________________________________________________________________Height = size(PIC,1);Width = size(PIC,2);randPoints = floor([rand(NUM,1)*Height,...    rand(NUM,1)*Width])+1;                  % 空间随机撒点allPoints = [StartPoint;EndPoint];          % 初始化可行点列表for i=1:NUM    if(PIC(randPoints(i,2),randPoints(i,1),1) == feasibleR  )        allPoints = [allPoints;double(randPoints(i,:))];    endend% 得到所有可行点列表for i = 1:size(allPoints,1)    scatter(allPoints(i,1),allPoints(i,2),'filled','SizeData',20,'MarkerFaceColor',[199 237 53]/255);    pause(.0005)end% 初始化无向图邻接矩阵%__________________________________________________________________________AdjacencyMatrix = genAM(PIC,allPoints);% 对矩阵AdjacencyMatrix使用【Dijkstra最短路径算法】；%__________________________________________________________________________

4 多目标规划

上面的问题无论约束条件有多复杂，目标都是只有一个。但是在现实中很多问题都能最终抽象为多目标优化问题。这是因为现实问题往往比较复杂，一般在达成目标时会权衡很多方面。这里简单介绍主流的几种方法。

多目标问题模型

•包含多个可能有冲突的目标函数•希望找到能够很好平衡全部优化目标的解集

理解多目标优化，需要先理解帕累托最优（Pareto Optimal）

帕累托最优

帕雷托最优是指资源分配的一种理想状态。给定固有的一群人和可分配的资源，如果从一种分配状态到另一种状态的变化中，在没有使任何人境况变坏的前提下，使得至少一个人变得更好，这就是帕雷托改善。

帕雷托最优的状态就是不可能再有更多的帕雷托改善的状态；换句话说，不可能在不使任何其他人受损的情况下再改善某些人的境况。

支配（Dominace）

当x1和x2满足如下条件时称x1支配x2： 对于所有目标函数x1不比x2差；至少在一个目标函数上，x1严格比x2要好；

(上图中点1支配点2；点5支配点1；点1和点4互不支配)

不可支配解集

（Non-dominated solution set） 当一个解集中任何一个解都不能被该集合中其他解支配，那么就称该解集为不可支配解集。

帕累托最优解集

（Pareto-optimal set） 所有可行解的不可支配解集被成为帕累托最优解集。

帕累托最优前沿面

（Pareto-optimal front） 帕累拖最优解集的边界（boundary）被成为帕累托最优前沿面。

多目标优化问题的经典方法有哪些？

线性加权法

其中权重代表了每个目标函数的重要程度。优点是简单；缺点是很难设定一个权重向量能够去获得帕累托最优解；在一些非凸情况不能够保证获得帕累托最优解。

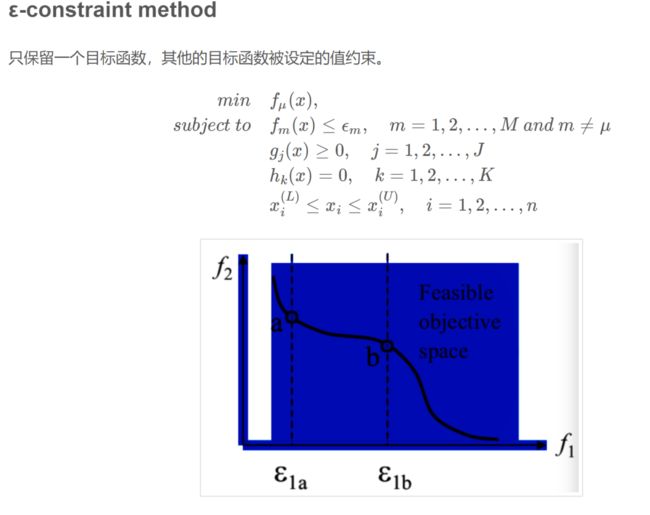
约束转化法

多目标遗传算法

基于遗传算法的多目标优化就是利用遗传算法的原理来搜索帕累托最优前沿面。关于遗传算法的介绍在往期推送已有，直接搜索历史推送即可。

其基本流程如下：

•随机产生初始群体;

•计算各点的目标函数值和约束函数值;

•根据目标函数值对群体分级;

•根据约束函数值和分级结果计算各点的约束罚项、劣解罚项及总罚项;

•根据各点的总罚项计算适应度;•根据各点的适应度,进行选择、交叉和变异操作,生成新群体;

•将总罚项为0的点放入非劣解集侯选表,对侯选表进行检查,保留第1级非劣点 , 删除其它点;

•检查是否收敛,如没有,转到步骤2;

•删除侯选表中与其它点距离太近的点;

•输出侯选表中的Pareto最优解集及对应的目标函数值;

•决策人根据个人偏好从Pareto最优解集中挑选出最适合该问题的解；

遗传算法相比与传统算法的优点是能够得到一个最优解集，而不是单单一个最优解，这样给我们更多的选择。但计算复杂度可能稍高，而且里面涉及的一些函数需要精心设计。