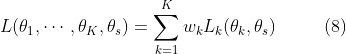paper学习笔记 - PLE
发于2020年，Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations | Papers With Code
摘要
然而，由于现实世界推荐系统中复杂且竞争的任务相关性，MTL模型往往会出现负迁移的性能退化（performance degeneration with negative transfer due to the complex and competing task correlation）。此外，通过对SOTA MTL模型的广泛实验，我们观察到了一个有趣的跷跷板现象（seesaw phenomenon），即一项任务性能的提升往往会损害其他一些任务的性能（that performance of one task is often improved by hurting the performance of some other tasks）。为了解决这些问题，我们提出了一种具有新颖共享结构设计的渐进分层提取（PLE：Progressive Layered Extraction）模型。PLE显式分离共享组件和任务特定组件，并采用渐进式路由机制逐步提取和分离更深层次的语义知识，提高了通用设置中跨任务的联合表示学习和信息路由的效率。（PLE separates shared components and task-specific components explicitly and adopts a progressive routing mechanism to extract and separate deeper semantic knowledge gradually, improving efficiency of joint representation learning and information routing across tasks in a general setup. ）
引言
推RS）需要包括各种用户反馈，以模拟用户兴趣并最大化用户参与度和满意度。然而，由于问题的高维性，用户满意度通常难以通过学习算法直接解决。同时，用户满意度和参与度有许多可以直接学习的主要因素，例如点击、完成、共享、偏爱和评论等的可能性。因此，在RS中应用多任务学习（MTL）来同时建模用户满意度或参与度的多个方面的趋势越来越大。事实上，它已成为主要行业应用的主流方法[11、13、14、25]。
MTL在一个单一模型中同时学习多个任务，并通过任务之间的信息共享提高学习效率[2]。然而，现实世界推荐系统中的任务通常是松散相关的，甚至是冲突的，这可能导致性能恶化，称为负迁移[21]。通过在现实世界中大规模视频推荐系统和公共基准数据集中的大量实验，我们发现，当任务相关性复杂且有时依赖于样本时，现有的MTL模型往往会牺牲其他任务的性能来改进某些任务，即与相应的单任务模型相比，多个任务无法同时改进，本文称之为跷跷板现象。
之前的工作更多地致力于解决负迁移，但忽略了跷跷板现象，例如，十字绣（cross-stitch network ）[16] 和水闸网络（sluice network） [18]建议学习静态线性组合以融合不同任务的表示，这无法捕获样本相关性。MMOE[13]基于输入应用门控网络来组合底层专家，以处理任务差异，但忽略了专家之间的差异和互动，这在我们的工业实践中被证明存在跷跷板现象。
为了实现这一目标，我们提出了一种新的MTL模型，称为渐进分层提取（PLE），该模型更好地利用共享网络设计中的先验知识来捕获复杂的任务相关性。与MMOE中的粗略共享参数相比，PLE显式分离共享专家和任务特定专家，以减轻公共知识和任务特定知识之间的有害参数干扰（PLE explicitly separates shared and task-specific experts to alleviate harmful parameter interference between common and task-specific knowledge）。此外，PLE引入了多层次专家和门控网络，并应用渐进分离路由从较低层次的专家中提取更深层次的知识，并逐步分离较高层次的任务特定参数（introduces multi-level experts and gating networks, and applies progressive separation routing to extract deeper knowledge from lower-layer experts and separate task-specific parameters in higher levels gradually）。
为了评估PLE的性能，我们在现实世界的工业推荐数据集和主要可用公共数据集（包括census-income [5], synthetic data [13] and Ali-CCP 1. ）上进行了广泛的实验。实验结果表明，PLE在所有数据集上都优于最先进的MTL模型，不仅在具有挑战性复杂相关性的任务组上，而且在不同场景下，在具有正常相关性的任务群上，都显示出了一致的改进。此外，腾讯大型视频推荐系统在线指标的显著改进表明了PLE在现实推荐应用中的优势。
主要贡献总结如下：
•通过在腾讯和公共基准数据集的大规模视频推荐系统中进行的大量实验，发现了一个有趣的跷跷板现象，即SOTA MTL模型往往以牺牲其他任务的性能为代价来改进某些任务，并且由于复杂的内在相关性，其性能并不优于相应的单任务模型。
•从联合表示学习和信息路由的角度，提出了一种具有新型共享学习结构的PLE模型，以提高共享学习效率，进而解决跷跷板现象和负迁移问题。除了推荐应用之外，PLE还可以灵活地应用于各种场景。
•进行了广泛的离线实验，以评估PLE在工业和公共基准数据集上的有效性。腾讯全球最大的内容推荐平台之一的在线A/B测试结果也表明，在现实应用中，PLE比SOTA MTL模型有了显著改善，观看次数增加了2.23%，观看时间增加了1.84%，从而产生了可观的业务收入。PLE已经成功地部署到推荐系统中，并且可以潜在地应用到许多其他推荐应用中。
相关工作
有效的多任务学习模型和MTL模型在推荐系统中的应用是与我们工作相关的两个研究领域。在本节中，我们将简要讨论这两个领域的相关工作。
2.1多任务学习模型
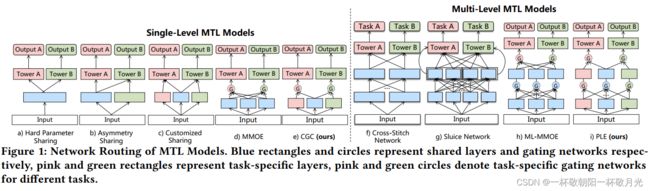
图1a中所示的硬参数共享[2]是最基本和最常用的MTL结构，但由于任务之间直接共享参数，可能会由于任务冲突而遭受负转移。为了处理任务冲突，图1f中的 cross-stitch network [16] in Fig. 1f) 和 sluice network [18]都建议学习线性组合的权重，以选择性地融合来自不同任务的表示。然而，对于这些模型中的所有样本，都是以相同的静态权重来进行组合的（representations are combined with the same static weights for all samples in these models），并且没有解决跷跷板现象。在这项工作中，所提出的PLE（渐进分层提取）模型应用具有门结构的渐进路由机制来融合基于输入的知识，从而实现不同输入的自适应组合。
已经有一些研究将门结构和注意力网络应用于信息融合。MOE[8]首先提出在底层共享一些专家，并通过一个门控网络组合专家。MMOE[13]扩展了MOE，为每个任务使用不同的门，以获得MTL中的不同融合权重。类似地，MRAN[24]应用多头自注意来学习不同特征集的不同表示子空间。专家和注意力模块在所有任务之间共享，并且在MOE、MMOE（如图1所示）和MRAN中没有特定于任务的概念。相比之下，我们提出的CGC（自定义门控制）和PLE模型将任务公共参数和任务特定参数显式分离，以避免复杂任务相关性导致的参数冲突。尽管MMOE在理论上有可能收敛到我们的网络设计中，但网络设计的先验知识很重要，MMOE在实践中很难发现收敛路径。Liu等人[10]应用任务特定注意网络来选择性地融合共享特征，但在注意网络融合之前，不同任务仍然共享相同的表示。以前的工作都没有明确解决表示学习和路由的联合优化问题，特别是以不可分割的联合方式，而这项工作首次尝试在联合学习和路由总体框架上提出一种新的渐进分离方式。
也有一些工作利用AutoML方法来寻找良好的网络结构。SNR框架[12]通过二进制随机变量控制子网络之间的连接，并应用NAS[26]搜索最优结构。类似地，Gumbel矩阵路由（ Gumbel-matrix routing ）框架[15]使用Gumbel Softmax技巧学习二进制矩阵。将路由过程建模为MDP，Rosenbaum等人[17]应用MARL[19]来训练路由网络。这些工作中的网络结构是在某些简化假设下设计的，不够通用。[17]中的路由网络为每个深度中的每个任务选择不超过一个功能块，这降低了模型的表达能力。Gumbel矩阵路由网络[15]对表示学习施加了约束，因为每个任务的输入需要在每个层合并为一个表示。此外，这些框架中的融合权重对于不同的输入是不可调整的，并且昂贵的搜索成本是这些方法寻找最优结构的另一个挑战。
2.2推荐系统中的多任务学习
为了更好地利用各种用户行为，多任务学习已广泛应用于推荐系统，并取得了实质性的改进。一些研究将传统的推荐算法（如协同过滤和矩阵分解）与MTL相结合。Lu等人[11]和Wang等人[23]对为推荐任务和解释任务学习的潜在表示进行正则化，以联合优化它们。Wang等人[22]将协同过滤与MTL相结合，以更有效地学习 user-item 相似度。与本文中的PLE相比，这些基于因子分解的模型表现出较低的表达能力，并且不能充分利用任务之间的共性。
作为最基本的MTL结构，硬参数共享已应用于许多基于DNN的推荐系统。ESSM[14]引入了两个辅助任务CTR（点击率）和CTCVR，并在CTR和CVR（转换率）之间共享嵌入参数，以提高CVR预测的性能。Hadash等人[7]提出了一个多任务框架，以同时学习排序任务和评分任务的参数。通过底部共享表示（sharing representations at the bottom），改进了[1]中的文本推荐任务。然而，在松散或复杂的任务关联下，硬参数共享往往会出现负迁移和跷跷板现象。相反，我们提出的模型引入了一种新的共享机制，以实现更有效的信息共享。
除了硬参数共享外，已有一些推荐系统使用具有更有效共享学习机制的MTL模型。为了更好地利用任务之间的相关性，Chen等人[3]利用hierarchical multi-pointer co-attention[20]来提高推荐任务和解释任务的性能。然而，每个任务的塔式网络在模型中共享相同的表示，这可能仍然存在任务冲突。[25]中的YouTube视频推荐系统将MMOE[13]通过不同的门控网络为每个任务组合共享专家，可以更好地捕捉任务差异并有效优化多个目标。与同等对待所有专家而不进行区分的MMOE相比，本文中的PLE明确地分离了任务公共专家和任务特定专家，并采用了一种新的渐进分离路由，在现实世界的视频推荐系统中实现了比MMOE更大的改进。
3.推荐MTL中的跷跷板现象
负迁移是MTL中的常见现象，尤其是对于松散相关的任务[21]。对于复杂的任务相关性，特别是样本相关的相关性模式，我们还观察到跷跷板现象，对于当前的MTL模型来说，在所有任务中提高共享学习效率并实现比相应的单任务模型的显著改进是困难的。在本节中，我们以腾讯的一个大型视频推荐系统为基础，全面介绍和研究了跷跷板现象。
3.1一种用于视频推荐的MTL排序系统
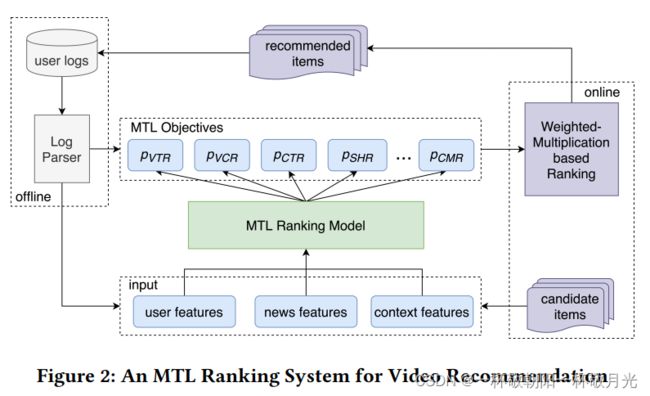
在本小节中，我们将简要介绍为腾讯新闻服务的MTL排序系统，该系统是世界上最大的内容平台之一，根据不同的用户反馈向用户推荐新闻和视频。如图2所示，在MTL排序系统中有多个目标来建模不同的用户行为，例如点击、分享和评论。在离线训练过程中，我们基于从用户日志中提取的用户行为来训练MTL排序模型。在每个在线请求之后，排序模型输出每个任务的预测，然后基于加权乘法的排序模块通过式1所示的组合函数将这些预测得分组合为最终得分，并最终向用户推荐排序靠前的视频。
其中每个w确定对应的预测得分的相对重要性，f(video_len)是非线性变换函数，例如对视频持续时间进行sigmoid函数或log函数变换。
和
是通过在线实验搜索优化的超参数，以最大化在线度量（maximize online metrics）。
在所有任务中，VCR（查看完成率）和VTR（浏览率）是两个重要的目标，分别为查看次数和观看时间的关键在线指标建模。具体地说，VCR预测是一个用MSE损失训练的回归任务，以预测每个视频的完成率。VTR预测是一项用交叉熵损失训练的二元分类任务，用于预测有效视频的概率，有效视频被定义为超过某个观看时间阈值的播放动作。VCR和VTR之间的相关模式是复杂的。首先，VTR的标签是播放动作和VCR的耦合因素，因为只有观看时间超过阈值的播放动作才会被视为有效视图。第二，播放动作的分布更加复杂，因为WIFI中设置了自动播放的场景的样本显示出更高的平均播放概率，而没有自动播放的显式点击场景的其他样本显示出更低的播放概率。由于复杂且强的样本相关模式，在对VCR和VTR进行联合建模时，观察到了跷跷板现象。
3.2 MTL中的跷跷板现象
为了更好地理解跷跷板现象，我们使用单任务模型和SOTA MTL模型对我们的排序系统中的VCR和VTR的复杂相关任务组进行了实验分析。除了硬参数共享、十字绣[16]、水闸网络[18]和MMOE[13]，我们还评估了两种新提出的结构，即不对称共享（asymmetric sharing）和定制共享（customized sharing）：
•非对称共享是一种新的共享机制，用于捕获任务之间的非对称关系。根据图1b），底层在任务之间不对称地共享，并且要共享的任务的表示（representation of which task）取决于任务之间的关系。常见的融合操作，如concatenation、sumpooling和average-pooling，可以应用于组合不同任务底层的输出。
•图1c中所示的定制共享）明确分离共享和任务特定参数，以避免固有冲突和负转移。与单任务模型相比，定制共享添加了共享底层以提取共享信息，并将共享底层和任务特定层的连接馈送到相应任务的塔式层。
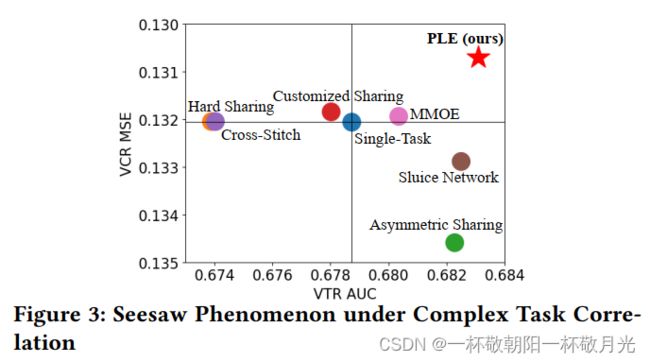
图3示出了实验结果，其中越 靠近右上角的气泡表示具有更高AUC和更低MSE即 更好性能。值得注意的是，AUC提升或MSE减少0.1%可以使 我们系统在线指标得到显著改善，这也在[4、6、14]中提到。可以看出，硬参数共享和十字绣网络遭受显著的负迁移，且在VTR中表现最差。通过创新共享机制捕获不对称关系，不对称共享在VTR中实现了显著改善，但在VCR中表现出显著退化，类似于水闸网络。由于共享层和任务特定层的显式分离，定制共享与单任务模型相比改善了VCR，但在VTR中仍有轻微退化。MMOE在两个任务上都优于单任务模型，但VCR的改进仅为+0.0001。尽管这些模型在这两个具有挑战性的任务中表现出不同的学习效率，但我们清楚地观察到跷跷板现象，即一个任务的改进往往导致另一个任务性能的下降，因为没有一个基线MTL模型完全位于第二象限。在公共基准数据集上使用SOTA模型的实验也显示出明显的拉锯现象。第5.2节将提供详细信息。
如上所述，VCR和VTR之间的关系复杂且依赖于样本。具体而言，VCR和VTR之间存在一些偏序关系，不同的样本表现出不同的相关性。因此，对于所有的样本十字绣和水闸网络通过相同的静态权重组合共享表示（ combine shared representations with same static weights for all samples），无法捕获样本相关性，并遭受跷跷板现象。MMOE基于输入用门来获得融合权重，在一定程度上处理任务差异和样本差异，这优于其他基线MTL模型。然而，在MMOE中，专家在所有任务之间无差别地共享，这无法捕获复杂的任务相关性，并且可能给某些任务带来有害噪声。此外，MMOE忽略了不同专家之间的交互，这进一步限制了联合优化的性能。除了VCR和VTR之外，在工业推荐应用中还有许多相关性复杂的任务，因为人类行为通常是微妙和复杂的，例如在线广告和电子商务平台中的CTR预测和CVR预测[14]。因此，考虑专家之间的差异和互动的强大网络对于消除复杂任务相关性 致的跷跷板现象至关重要。
在本文中，我们提出了一种渐进分层提取（PLE）模型来解决跷跷板现象和负迁移。PLE的关键思想如下。首先，它明确地分离共享专家和任务特定专家，以避免有害的参数干扰。其次，引入多级专家和门控网络来融合更抽象的表示。最后，它采用一种新的渐进分离路由来建模专家之间的交互，并在复杂相关任务之间实现更高效的知识转移。如图3所示，PLE在两个任务中都比MMOE有显著改进。第4节和第5节将分别描述结构设计和实验的细节。
4 递进分层提取
为了解决跷跷板现象和负迁移，我们在本节中提出了一种渐进分层提取（PLE：Progressive Layered Extraction）模型，该模型具有新颖的共享结构设计。首先，提出了一种显式分离共享专家和任务专家的自定义门控制（CGC：Customized Gate Control）模型。其次，将CGC扩展为具有多级门控网络和渐进分离路由的广义PLE模型，以实现更有效的信息共享和联合学习。最后，对损失函数进行了优化，以更好地应对MTL模型联合训练的实际挑战。
4.1Customized Gate Control
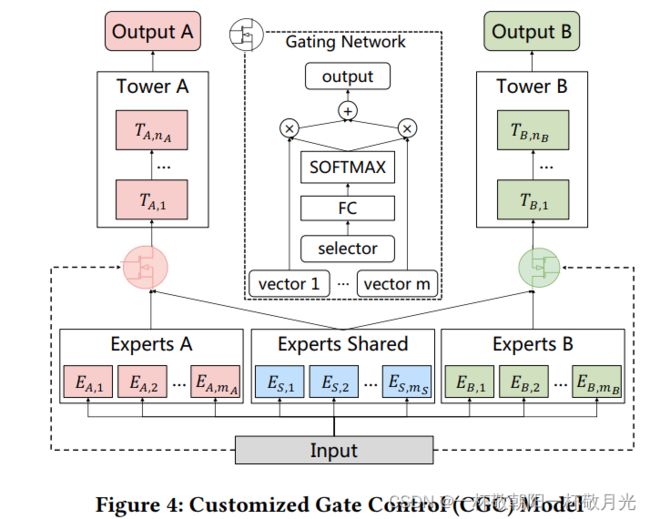
基于通过显式分离共享层和任务特定层实现与单任务模型类似性能的定制共享，我们首先引入了定制的门控制（CGC）模型。如图4所示，底部有一些专家模块，顶部有一些特定于任务的塔式网络。每个专家模块由称为专家的多个子网络组成，每个模块中的专家数量是超参数。类似地，塔式网络也是多层网络，其宽度和深度是超参数。具体而言，CGC中的共享专家负责学习共享模式，而特定任务的模式由特定任务专家提取。每个塔式网络从共享专家和其自己的特定任务专家那里吸收知识，这意味着共享专家的参数受所有任务的影响，而特定任务专家的参数仅受相应特定任务的影响。
在CGC中，共享专家和任务特定专家通过门控网络进行选择性融合。如图4所示，选通网络的结构基于单层前馈网络，用SoftMax作激活函数，输入作为选择器以计算所选向量的加权和，即专家的输出。更准确地说，任务k的选通网络的输出公式为：
其中
是输入向量，
是加权函数，通过线性变换和SoftMax层计算任务k的权重向量：
其中
是参数矩阵，
和
分别是共享专家和任务k特定专家的数目，
是输入向量的维度。
是选择矩阵（selected matrix），由所有的共享专家和任务k的特定专家的输出向量构成（is a selected matrix composed of all selected vectors including shared experts and task k’s specific experts）：
![S^{k}(x) = [E^{T}_{(k,1)},E^{T}_{(k,2)},\cdots,E^{T}_{(k,m_{k})}, E^{T}_{(s,1)},E^{T}_{(s,2)},\cdots,E^{T}_{(s,m_{s})} ] \ \ \ \ \ \ \ \ \ (4)](http://img.e-com-net.com/image/info8/2e78c071e3f14b82b26df2c07e3fd9ab.gif){kind=small}
最后，任务k的预测为：
其中
表示任务k的塔式网络。
与MMOE相比，CGC消除了任务的塔式网络和其他任务的特定专家之间的连接，使不同类型的专家能够集中精力高效地学习不同的知识，而不受干扰。结合门控网络基于输入动态融合表示的优势，CGC在任务之间实现了更灵活的平衡，并更好地处理任务冲突和样本相关关系。
4.2渐进分层提取
CGC显式地分离任务特定组件和共享组件。然而，学习需要在深度MTL中逐渐形成越来越深的语义表示，而通常不清楚中间表示应被视为共享的还是任务特定的。为了解决这个问题，我们将CGC推广为渐进分层提取（PLE）。如图5所示，在PLE中存在多级提取网络以提取higher-level共享信息。除了任务特定专家的门之外，提取网络还为共享专家网络提供了一个门控网络以组合该层所有专家网络（the extraction network also employs a gating network for shared experts to combine knowledge from all experts in this layer）。因此，PLE中不同任务的参数在早期层不像CGC那样完全分离，而是在上层逐渐分离。高层提取网络中的选通网络将低层提取网络中选通的融合结果作为选择器，而不是原始输入（The gating networks in higher-level extraction network take the fusion results of gates in lower-level extraction network as the selector instead of the raw input），因为它可以为高层专家提取的抽象知识提供更好的信息（as it may provide better information for selecting abstract knowledge extracted in higher-level experts）。
PLE中加权函数（weighting function）、选择矩阵（selected matrix）和选通网络（gating network）的计算与CGC中相同。具体而言，PLE的第j个提取网络中任务k的选通网络的公式为：
是任务k的加权函数（weighting function），其输入是上一层选通网络的融合结果
,
是任务k的第j个宣统网络的选择矩阵。值得注意的是，PLE中共享模块的选定矩阵与任务特定模块略有不同，因为它由该层中的所有共享专家和任务特定专家组成。
在计算所有门控网络和专家后，我们最终可以获得PLE中任务k的预测：
通过多级专家和门控网络，PLE提取并组合每个任务的深层语义表示，以提高泛化能力。如图1所示，路由策略是MMOE的完全连接和CGC的早期分离。不同的是，PLE采用渐进分离路由来吸收来自所有下层专家的信息，提取higher-level共享知识，并逐步分离特定于任务的参数。逐步分离的过程类似于化学中从化合物中提取所需产物的过程。在PLE中的知识提取和转换过程中，较低级别的表示被联合提取/聚合并路由到较高级别的共享专家，获得共享的知识并逐步分配到特定的塔层，从而实现更高效和灵活的联合表示学习和共享（ During the process of knowledge extraction and transformation in PLE, lower-level representations are jointly extracted/aggregated and routed at the higher-level shared experts, obtaining the shared knowledge and distributing to specific tower layers progressively, so as to achieve more efficient and flexible joint representation learning and sharing）。虽然MMOE的全连接路由看起来像是CGC和PLE的一般设计，但第5.3节中的实际研究表明，尽管存在可能性，但MMOE无法收敛到CGC或PLE的结构。
4.3 Joint Loss Optimization for MTL
在设计了高效的网络结构之后，我们现在将重点放在以端到端的方式联合训练任务特定和共享层。在多任务学习中，联合损失的常见公式是每个单独任务的损失的加权和：
其中
表示共享参数，
表示任务数目，
和
分别是损失函数，损失函数的权重，任务k特定的参数。
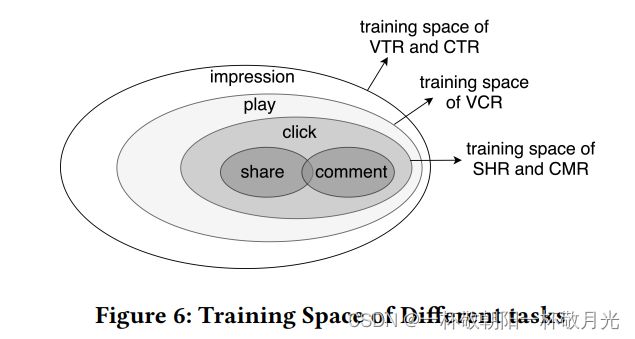
然而，存在若干问题，使得MTL模型的联合优化在实践中具有挑战性。在本文中，我们优化了联合损失函数，以解决现实世界推荐系统中遇到的两个关键问题。第一个问题是由于用户连续操作导致的异构样本空间（The first problem is the heterogeneous sample space due to sequential user actions）。例如，用户只能在点击某个项目后对其进行共享或评论，这导致图6所示的不同任务的不同样本空间。为了联合训练这些任务，我们将所有任务的样本空间的并集视为整个训练集，并在计算每个单独任务的损失时忽略其自身样本空间之外的样本：
其中，
是样本i在任务k的基于预测
和实际标签
损失函数，
表示样本i是否在任务k的样本空间中。
第二个问题是，MTL模型的性能对训练过程中损失权重的选择非常敏感[9]，因为它决定了每个任务对联合损失的相对重要性。在实践中，观察到每个任务在不同的训练阶段可能具有不同的重要性。因此，我们将每个任务的损失权重视为动态权重，而不是静态权重。首先，我们为任务k设置初始损失权重
，每步根据更新比率
更新权重:
表示训练步数（training epoch），和是模型的超参数。
5 EXPERIMENTS
在本节中，在腾讯的大规模推荐系统和公共基准数据集上进行了广泛的离线和在线实验，以评估所提出模型的有效性。我们还分析了所有基于门的MTL模型中的专家利用率，以更好地理解门网络的工作机制，并进一步验证CGC和PLE的结构值。
5.1 Evaluation on the Video Recommender System in Tencent
在本小节中，我们在腾讯视频推荐系统中对具有复杂和正常相关性的任务组以及多个任务进行离线和在线实验，以评估所提出模型的性能。
5.1.1数据集。我们通过对腾讯新闻视频推荐系统的连续8天的用户日志进行采样，收集了一个行业数据集。数据集中有4692.6万用户、268.2万视频和9.95亿样本。如前所述，VCR、CTR、VTR、SHR（分享率）和CMR（评论率）是在数据集中建模用户偏好的任务。
5.1.2基线模型。在实验中，我们将CGC和PLE与单任务模型、不对称共享（asymmetric sharing）、定制共享（customized sharing）以及包括十字交叉网络、水闸网络和MMOE的SOTA MTL模型进行了比较。由于多级专家在PLE中共享，我们通过添加多级专家进行公平比较，将MMOE扩展到图1h所示的ML-MMOE（多层MMOE）。在ML-MMOE中，高级专家通过门控网络组合来自低级专家的表示，所有门控网络共享同一选择器。
5.1.3实验设置。在实验中，VCR预测是用MSE损失训练和评估的回归任务，建模其他任务都是用交叉熵损失训练和用AUC评估的二元分类任务。前7天的样本用于训练，其余样本为测试集。在MTL模型和单任务模型中我们采用三层MLP网络，激活函数采用relu，隐藏层大小[256、128、64]。对于MTL模型，我们将专家实现为单层网络，并调整以下特定于模型的超参数：number of shared layers, cross-stitch units in hard parameter sharing and cross-stitch network, number of experts in all gate-based models.为了公平比较，我们将所有多级MTL模型实现为两级模型，以保持相同的网络深度。
除了常见的评估指标（如AUC和MSE）外，我们还定义了一个MTL增益指标，以定量评估多任务学习相对于单个任务模型对特定任务的提升。如式11所示，对于给定任务组和MTL模型q，任务a上q的MTL增益被定义为任务a相对于具有相同网络结构和训练样本的单个任务模型的MTL模型的性能改进。
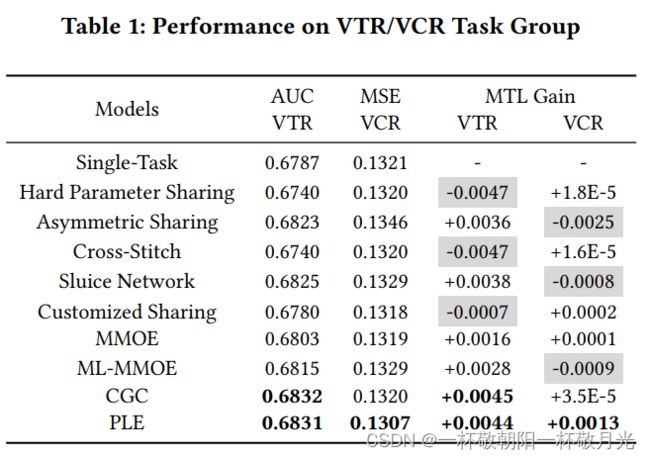
5.1.4对具有复杂相关性的任务进行评估。为了更好地捕捉主要的在线参与指标，例如观看次数和观看时间，我们首先在VCR/VTR的任务组上进行实验。表1说明了实验结果，我们用粗体标记最佳分数，用灰色标记性能退化（负MTL增益）。结果表明，在VTR中，CGC和PLE明显优于所有基线模型。由于VTR和VCR之间的复杂相关性，我们可以清楚地观察到锯齿状灰色分布的跷跷板现象，即一些模型改善了VCR但损害了VTR，而一些模型改善VTR却损害了VCR。具体而言，MMOE相比各自的单个任务使得两个任务均有提升，但改善并不显著，而ML-MMOE改善了VTR，但损害了VCR。与MMOE和ML-MMOE相比，CGC对VTR的改善更大，对VCR的改善也很小。最后，PLE以类似的速度收敛，并在具有最佳VCR MSE和最佳VTR AUC之一的上述模型上实现了显著改进。
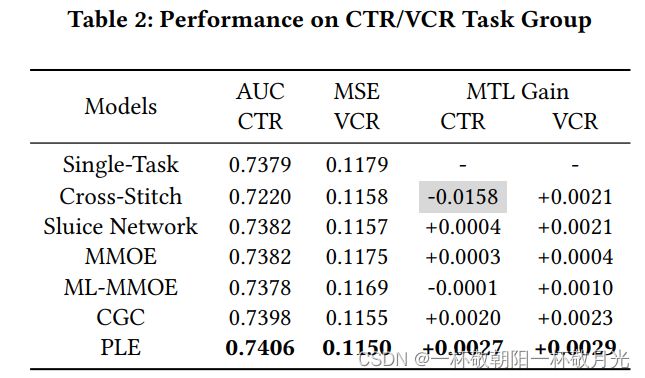
5.1.5对具有正常相关性的任务的评估。尽管CGC和PLE在具有非常复杂相关性的任务上表现良好，但我们在具有正常相关性模式的CTR/VCR的一般任务组上进一步验证了它们的通用性。由于CTR和VCR旨在模拟不同的用户行为，它们之间的关联更简单。如表2所示，除十字绣外的所有模型在两个任务中均显示出正的MTL增益，这表明CTR和VCR之间的相关模式并不复杂，也不会出现跷跷板现象。在这种情况下，CGC和PLE在两个任务上仍显著优于所有SOTA模型，具有出色的MTL增益，这证明CGC和PPE的好处是普遍的，实现了更好的共享学习效率，并在广泛的任务相关情况下持续提供增量性能改进，不仅适用于难以协作的复杂关联任务，也适用于一般相关性的任务。
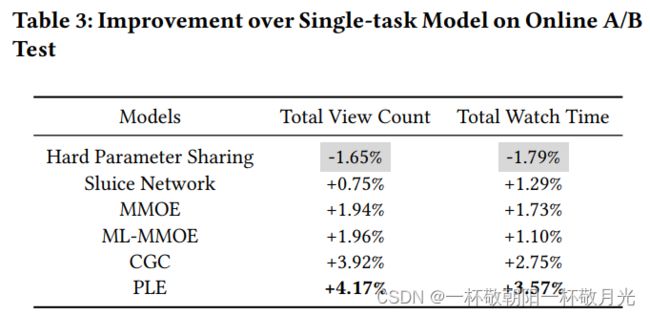
5.1.6在线A/B测试。在视频推荐系统中，对VTR和VCR任务组进行了为期4周的在线A/B测试。我们在基于C++的深度学习框架中实现所有MTL模型，将用户随机分配到几个桶中，并将每个模型部署到其中一个桶中。通过第3节中描述的多个预测得分的组合函数获得最终排序得分。表3显示了MTL模型在每个用户的总观看次数和每个用户的观看时长（系统的最终目标）的在线指标上优于单任务模型。结果表明，与所有基线模型相比，CGC和PLE实现了在线度量的显著增加。此外，PLE在所有在线指标上都显著优于CGC，这表明MTL中AUC或MSE的微小改善会显著改善在线指标。此后，PLE已部署到腾讯的平台上。
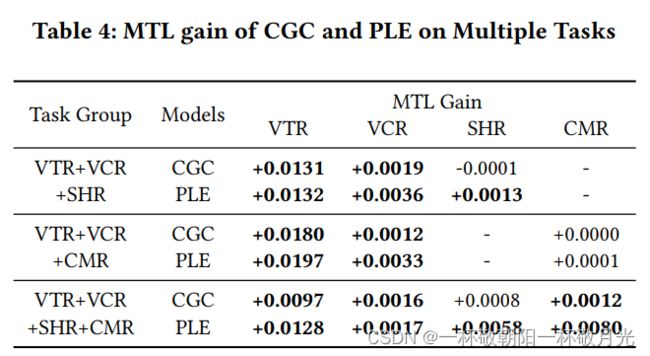
5.1.7多任务评估。最后，我们探讨了CGC和PLE在具有多个任务的更具挑战性的场景中的可扩展性。除了VTR和VCR之外，我们还引入了SHR（共享率）和CMR（评论率）来模拟用户反馈行为。它可以灵活地将CGC和PLE扩展到多个任务案例，只需为每个任务添加特定于任务的专家模块、门控网络和塔式网络。如表4所示，CGC和PLE在几乎所有任务组的所有任务上都比单任务模型有显著改进。这表明，CGC和PLE仍然显示出促进任务合作、防止负迁移和具有两个以上任务的一般情况下的跷跷板现象的益处。在所有情况下，PLE均显著优于CGC。因此，PLE在提高不同规模任务组的共享学习效率方面表现出更强的优势。
5.2 Evaluation on Public Datasets
在本小节中，我们在公共基准数据集上进行实验，以进一步评估PLE在推荐之外的场景中的有效性。
5.2.1数据集。
•根据[13]的数据合成过程生成合成数据，以控制任务相关性。由于[13]中未提供数据合成的超参数，我们按照标准正态分布对αi和βi进行随机采样，并将c=1、m=10、d=512设置为再现性。每个相关性生成140万个具有两个连续标签的样本。
• Census-income数据集[5]包含从1994年人口普查数据库中提取的299285个样本和40个特征。为了与基线模型进行公平比较，我们考虑与[13]相同的任务组。具体而言，任务1旨在预测收入是否超过50K，任务2旨在预测此人的婚姻状况是否从未结婚。
•Ali-CCP数据集1是一个公共数据集，包含从淘宝推荐系统中提取的8400万个样本。CTR和CVR（转换率）是两个任务，用于对数据集中的点击和购买行为进行建模。
5.2.2实验设置。Census-income数据集的设置与[13]相同。对于合成数据和Ali-CCP数据集，我们采用三层MLP网络，在MTL模型和单任务模型中，采用RELU激活、隐藏层大小均为[256、128、64]。超参数的调整与第5.1节中的实验类似。
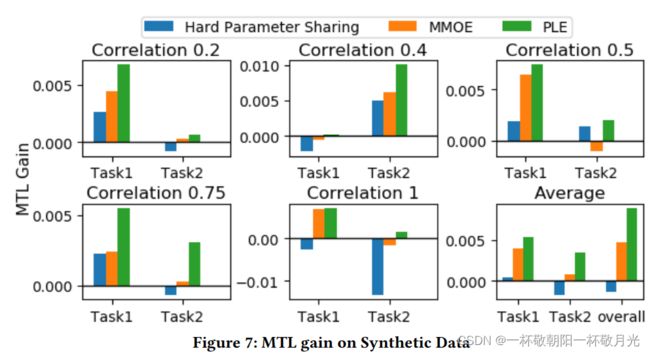
5.2.3实验结果。图7所示的合成数据的实验结果表明，硬参数共享和MMOE有时会出现跷跷板现象，并在两个任务之间失去平衡。相反，PLE在不同相关性的两项任务中始终表现最佳，平均MTL增益比MMOE提高87.2%。如表5所i-CCP和Census-income数据集的结果表明，PLE消除了跷跷板现象，并在两项任务上始终优于单任务模型和MMOE。
结合之前在工业数据集和在线A/B测试上的实验，PLE在不同任务关联模式和不同应用程序下提高MTL效率和性能方面表现出稳定的总体效益。
5.3 Expert Utilization Analysis
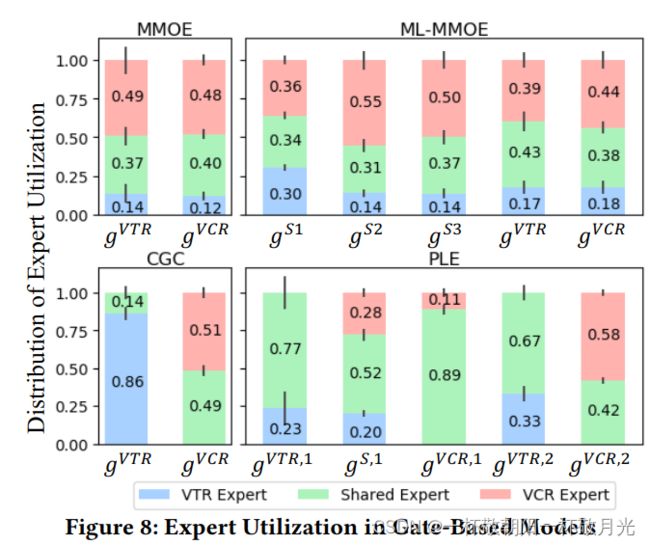
为了揭示专家是如何通过不同的门聚集的，我们研究了工业数据集VTR/VCR任务组中所有基于门的模型的专家利用率。为了简单和公平的比较，我们将每个专家视为单层网络，在CGC和PLE的每个专家模块中只保留一名专家，而在MMOE和ML-MMOE的每个层中保留三名专家。图8显示了所有测试数据中每个门使用的专家的权重分布，其中条形高度和垂直短线分别表示权重的平均值和标准偏差。结果表明，VTR和VCR结合了CGC中具有显著不同权重的专家，而MMOE中的权重非常相似，这表明设计良好的CGC结构有助于实现不同专家之间的更好区分。此外，MMOE和ML-MMOE中的所有专家都不存在零权重，这进一步表明，尽管存在理论上的可能性，但在实践中，在没有先验知识的情况下，MMOE与ML-MMEE很难收敛到CGC和PLE的结构。与CGC相比，PLE中的共享专家对塔式网络的输入有更大的影响，尤其是对于VTR任务。PLE比CGC表现得更好的事实表明了共享更高级别更深层表示的价值。换句话说，要求任务之间共享某些更深层次的语义表示，因此渐进分离路由提供了更好的联合路由和学习方案（In other words, it is demanded that certain deeper semantic representations are shared between tasks thus a progressive separation routing provides a better joint routing and learning scheme）。
6 CONCLUSION
在本文中，我们提出了一种新的MTL模型，称为递进分层提取（PLE），它显式地分离任务共享和任务特定参数，并引入了一种创新的递进路由方式，以避免负迁移和跷跷板现象，实现更有效的信息共享和联合表示学习。在工业数据集和公共基准数据集上的离线和在线实验结果表明，与SOTA MTL模型相比，PLE有显著和一致的改进。探索分层任务组相关性将是未来工作的重点。