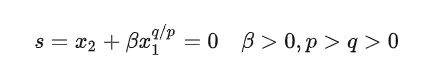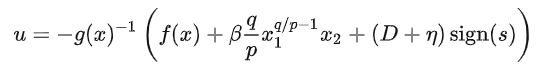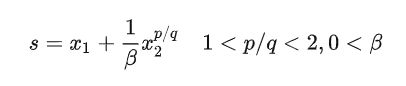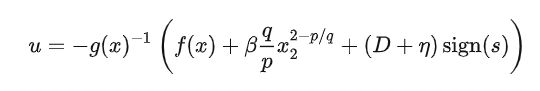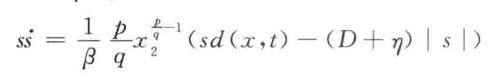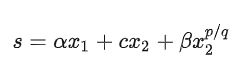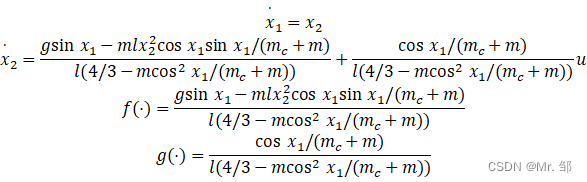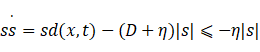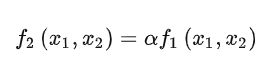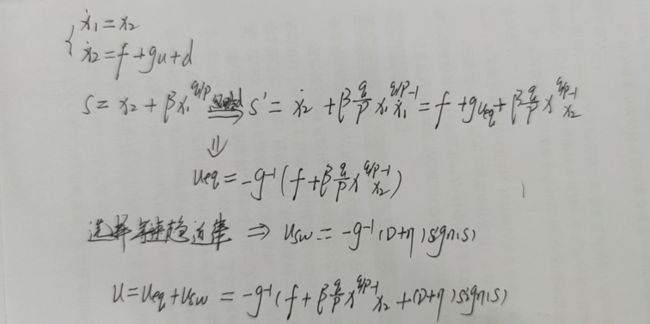VSC/SMC(十三)——快速和非奇异Terminal滑模控制(含程序模型)
目录
前言
1.Terminal滑模控制
1.1 传统Terminal滑模
1.2非奇异Terminal滑模
1.3 非奇异快速Terminal滑模
2.传统Terminal滑模
2.1 控制器设计
3.非奇异终端滑模控制
3.1 控制器设计
3. 仿真分析
3.1 被控对象
3.2 S函数编写被控对象
3.3 模型
3.4 仿真结果分析
3.4.1 快速终端滑模控制
3.4.2 非奇异终端滑模控制
3.5 有限时间稳定分析
3.5.1 切换面s稳定时间分析
3.5.2程序
3.5.3输出结果
3.5.4 状态变量x稳定时间分析
3.5.5程序
3.5.6 输出结果
3.6 关于相轨迹绘制
4 结论
5.补充
前言
上篇文章提到了Terminal终端滑模控制:
VSC/SMC(十二)——非线性系统的终端(terminal)滑模控制(含程序模型)_Mr. 邹的博客-CSDN博客
那为什么又要引入快速和非奇异终端滑模控制呢?
①传统的终端滑模控制由于引入非线性部分,改善了向平衡状态收敛的速度,而且越远离平衡状态收敛速度越快,但因为实际上由于传统终端滑模面的设计使得终端滑膜控制在接近平衡状态时,收敛速度比线性滑模控制速度要慢,所以收敛时间会更长。简单的说就是传统的终端滑模控制能改进收敛速度但是可能会增加收敛时间,只能做到快速渐进收敛,所以希望继承收敛速度的优点并且要减少收敛时间。
往期文章:
基于LMI的线性化系统控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
基于LMI的线性系统滑模鲁棒控制_Mr. 邹的博客-CSDN博客
使用hinfric和hinflmi函数设计H∞输出反馈控制器(含白嫖代码)_Mr. 邹的博客-CSDN博客
VSC/SMC(一)——基于趋近律的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客_滑模面的选取
VSC/SMC(二)——基于趋近律的滑模鲁棒控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(三)——基于饱和切换函数的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(四)——基于线性化反馈的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(五)——基于参考模型的滑模控制_Mr. 邹的博客-CSDN博客
基于参考模型的主动悬架滑模控制(详细滑模控制推导)_Mr. 邹的博客-CSDN博客
VSC/SMC(六)——基于低通滤波器的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(七)——基于高增益观测器的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(八)——基于慢时变干扰观测器的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客_慢时变干扰观测器 SMC/VSC(九)——控制器容错自适应滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(十)——主辅电机的协调滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
SMC/VSC(十一)——基于趋近律的离散滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客
想学好滑模控制器和LMI控制的的同学,欢迎白嫖我的程序和模型!
1.Terminal滑模控制
1.1 传统Terminal滑模
其中,p和q为正奇数。
问题:
①由于非线性项的引入,所以越是远离平衡点,收敛速度越快,而在接近平衡点时,收敛速度变慢,甚至比线性滑模面还要慢
②由于滑模面设计非线性项是x1^(q/p),导致存在奇异点问题,这里先给出后面要推导的传统快速终端滑模控制律:
可以看到,当x1 = 0,而x2≠0时,因为q/p-1 > 0,所以此时出现奇异点。
1.2非奇异Terminal滑模
其中,p和q为正奇数。
特点:解决了奇异点问题,但是快速收敛的问题还没有解决。
同理这里先给出非奇异快速终端滑模控制律:
可以看到由于p/q<2,所以控制律中x2的幂次是大于0的。
为什么要p/q>1?
这里先给出后续稳定性分析的Lyapunov证明结论:
可以看到p/q>1使得x2^(p/q-1) > 0,而|d| < D,所以使得V' = ss' < 0,保证稳定性证明。
1.3 非奇异快速Terminal滑模
其中,p > q,且p和q为正奇数。
特点:非线性项保证系统状态在远离平衡状态较大时能快速趋近平衡状态,线性项使系统状态在接近平衡状态时快速收敛;而且由于非线性项x2^(p/q),得到的控制律能保证不出现奇异点问题。
2.传统Terminal滑模
2.1 控制器设计
3.非奇异终端滑模控制
3.1 控制器设计
对于普通终端滑模控制、快速终端滑模控制、非奇异终端滑模控制的理解我还不到位,推荐一下博主链接:
滑模变结构控制 - 知乎
3. 仿真分析
3.1 被控对象
其中,x1和x2为倒立摆系统的角度和角速度,取小车质量mc = 1kg,摆杆质量m = 0.1kg,摆杆长度l = 0.5m。
3.2 S函数编写被控对象
选取扰动dt = 2*sin(t),初始位置[pi/60 0]'。
function [sys,x0,str,ts]=Plant(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9 }
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[pi/60 0]';%倒立摆初始状态
str=[];
ts=[];
function sys=mdlDerivatives(t,x,u)
g=9.8;mc=1.0;m=0.1;l=0.5;
S=l*(4/3-m*(cos(x(1)))^2/(mc+m));
fx=g*sin(x(1))-m*l*x(2)^2*cos(x(1))*sin(x(1))/(mc+m);
fx=fx/S;
gx=cos(x(1))/(mc+m);
gx=gx/S;%g(x,t),用gx是因为怕和重力加速度g混淆
U = u(2);
dt = u(1);
dx1=x(2);%x1'
dx2=fx+gx*U+dt;%x2'
sys = [dx1;dx2];
function sys=mdlOutputs(t,x,u)
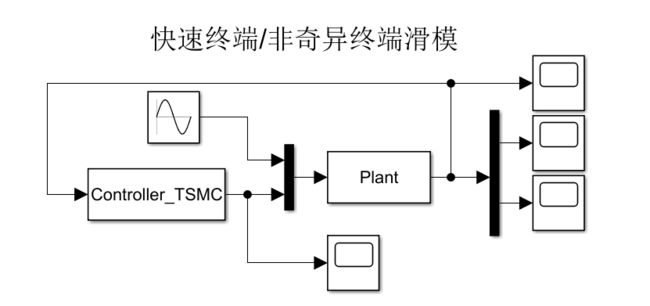
sys = x;3.3 模型
3.4 仿真结果分析
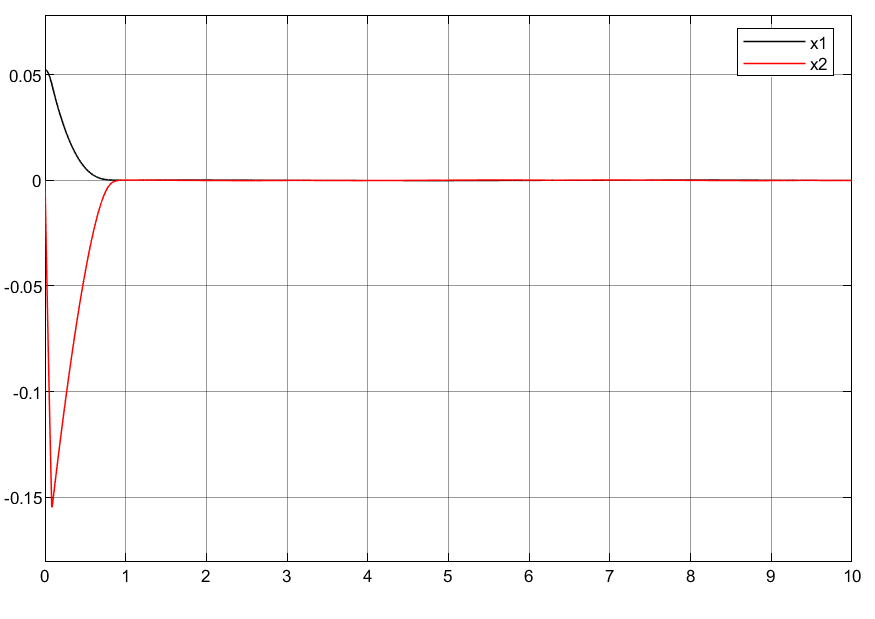
3.4.1 快速终端滑模控制
追踪效果
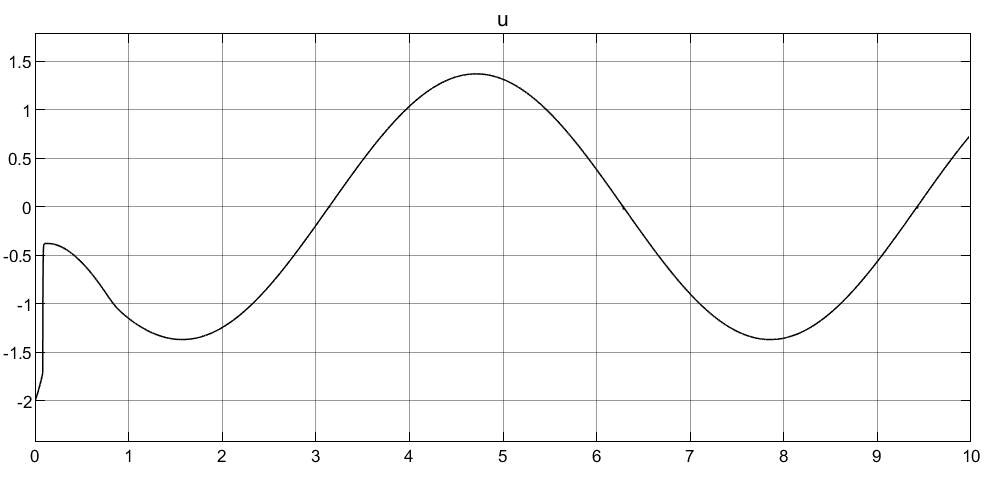
控制输入
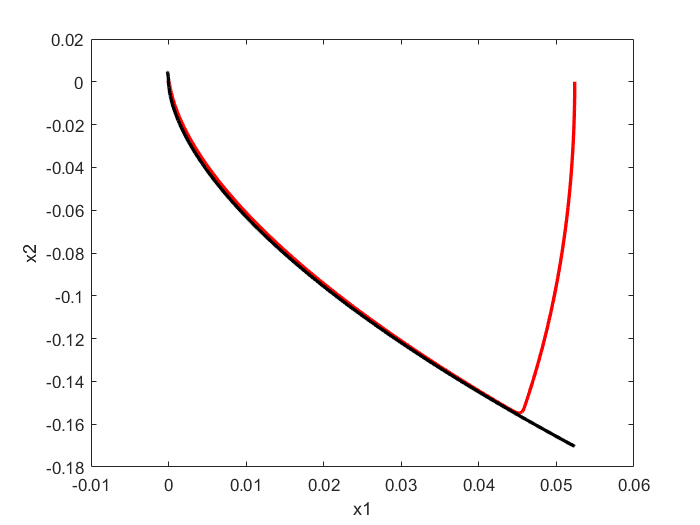
相轨迹
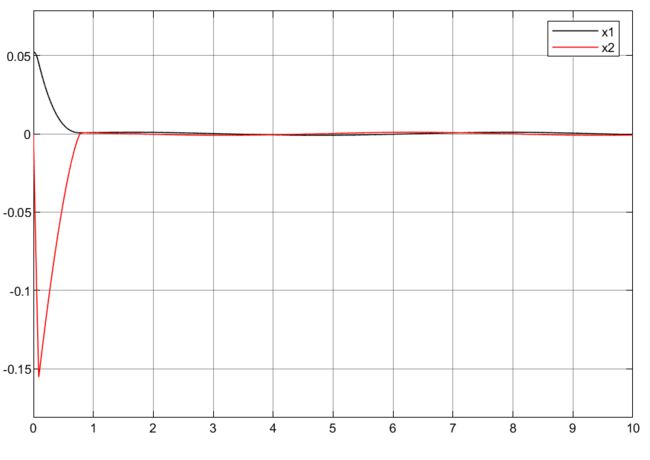
3.4.2 非奇异终端滑模控制
追踪效果
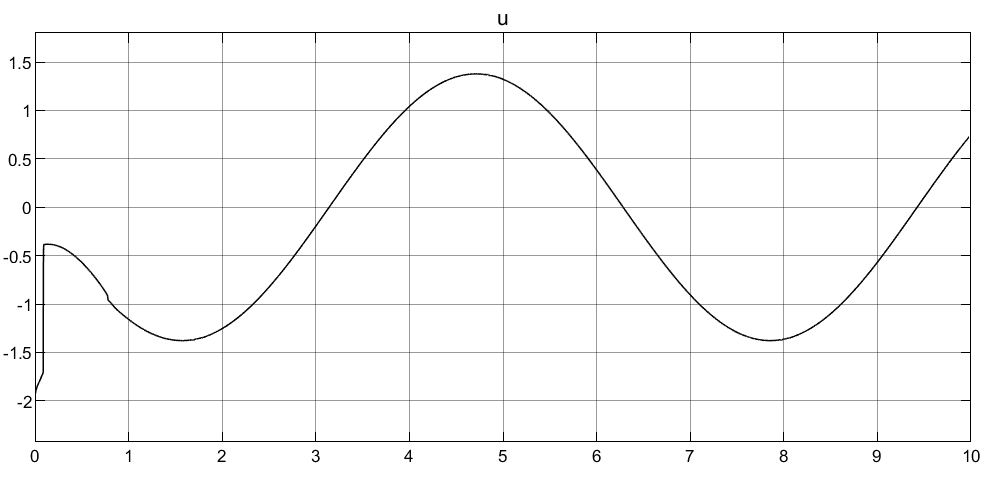
控制输入
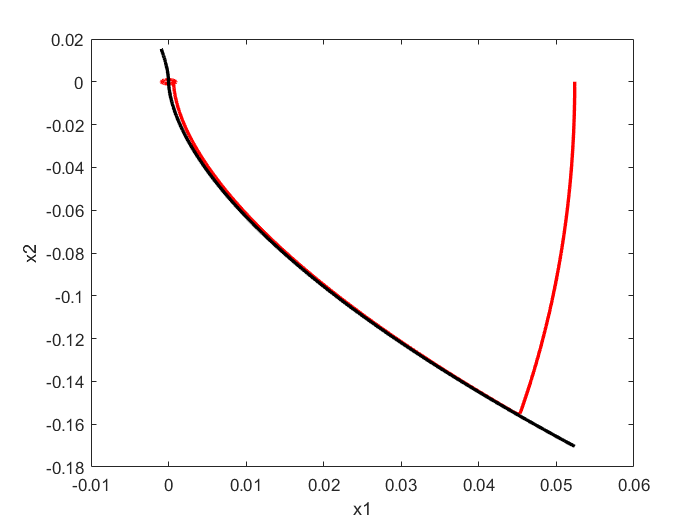
相轨迹
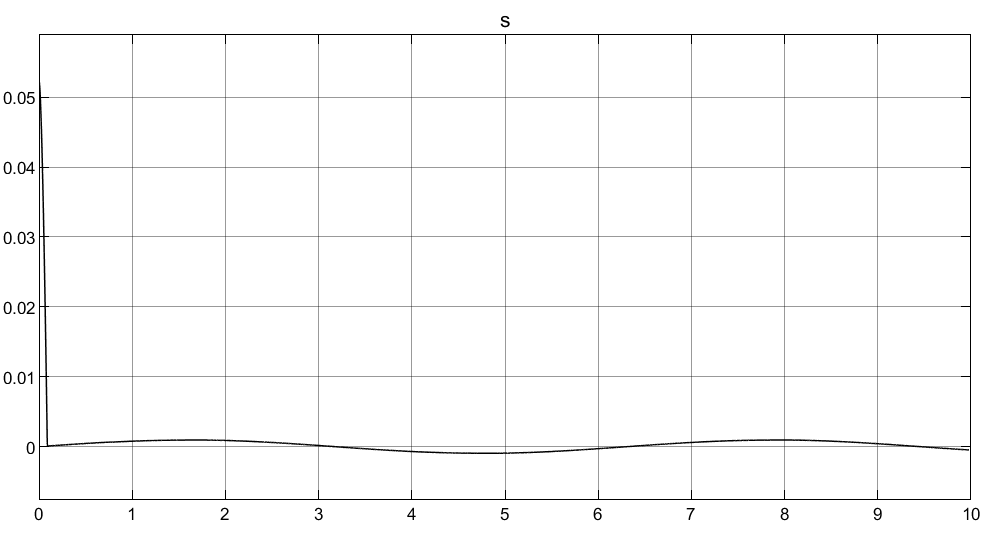
切换面
3.5 有限时间稳定分析
3.5.1 切换面s稳定时间分析
从上面的Lyapunov稳定性分析中已经有:
得到从切换面s初始状态s(0)到s = 0的时间为tr。
3.5.2程序
eta = 0.1;
tr = abs(s(1,2)/eta);
sprintf('切换函数s初始状态s(0)到达s = 0平衡的时间为: %fs',tr)3.5.3输出结果
ans =
'切换函数s初始状态s(0)到达s = 0平衡的时间为: 0.523599s'
3.5.4 状态变量x稳定时间分析
得到从状态变量x初始状态x(tr)到x(ts+tr) = 0的时间为ts。
3.5.5程序
q = 3;p = 5;beta = 1;
ts = p/(beta*(p-q))*(pi/60)^(1-q/p);
sprintf('从初始状态到达平衡的时间为: %fs',ts)3.5.6 输出结果
ans =
'从初始状态到达平衡的时间为: 0.768315s'
3.6 关于相轨迹绘制
非线性系统相轨迹的分析与绘制详解 - 知乎
其实原理很简单,就是理想时候假设滑模动态s' = 0,化简成:
这样的相关形式,然后x轴定义为x1(当滑模变量为状态变量时),或e(当滑模变量为误差变量时),
y轴定义为f2(x1,x2)和α*f1(x1,x2),程序如下:
M=2;
q=3;p=5;
if M==1 %TSM
plot(x1(:,2),x2(:,2),'r',x1(:,2),-(abs(x1(:,2))).^(q/p).*sign(x1(:,2)),'k','linewidth',2);
elseif M==2 %NTSM
plot(x1(:,2),x2(:,2),'r',x1(:,2),(abs(-x1(:,2))).^(q/p).*sign(-x1(:,2)),'k','linewidth',2);
end
xlabel('x1');ylabel('x2');4 结论
可以看到快速滑模控制和非奇异终端滑模控制得跟踪效果和控制力基本相同,但是从相轨迹上来看,都能快速趋于0,且好像非奇异终端滑模控制在靠近原点处有波动,感觉效果在这里更差些。
学习问题:
①在编写控制器时的程序时,滑模面和控制律要相应的为如下形式,否则报错或者不收敛?
快速Terminal滑模面:
相应的控制力:
非奇异终端滑模面:
相应的控制力:
即在原文的基础上加了绝对值和sign符号函数,这样才能仿真出和书上相同的结果。
②为什么p和q一定要是奇数?
5.补充
好几个同学私信我控制律如何通过滑模面推出来的,我最开始的几篇文章都有,为了方便学习,那么我在这里再给大家手动推一边(公式太难编辑了,字丑勿怪哈),以传统终端滑模趋近律为例:
如果有帮助,麻烦帮忙点个赞是我最大的分享动力,非常感谢!
注:仅为便利自己学习,错误在所难免,如有侵权,请联系删除,有兴趣的学者可以参考学习交流,谢谢!
参考资料:
《Terminal sliding mode control of MIMO linear systems ---Man Zhihong; Xing Huo Yu》
《滑模变结构控制MATLAB仿真:基本理论与设计方法第四版》---刘金琨