【机器学习】PCA主成分项目实战：MNIST手写数据集分类

手动反爬虫：原博地址 https://blog.csdn.net/lys_828/article/details/122651759

 知识梳理不易，请尊重劳动成果，文章仅发布在CSDN网站上，在其他网站看到该博文均属于未经作者授权的恶意爬取信息

什么是PCA

在多元统计分析中，主成分分析（Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。具体地，主成分可以看做一个线性方程，其包含一系列线性系数来指示投影方向。

注意PCA针对的是数据处理。在实际中会遇到数据问题：（1）数据过少；（2）数据过多。

数据过少最靠谱的方式就是增加数据量， 而对于数据量过多时，需要有一种方法快速的帮助我们判断数据的价值，PCA就可以帮助我们选择出主要的成分。

PCA处理手写数字集

1 模块加载与数据导入

导入常用模块

from sklearn.model_selection import train_test_split
import pandas as pd

MNIST手写数字数据库的训练集为60,000个示例，测试集为10,000个示例。它是NIST更大集合的子集。这些数字已进行尺寸规格化，并在固定尺寸的图像中居中。

对于想要尝试在真实数据上尝试学习技术和模式识别方法而又不花太多精力进行预处理和格式化的人们来说，这是一个很好的数据库。

数据导入的方式如下。

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, cache=True)
mnist.data.shape

输出结果如下。

一共有70000条数据，每条数据中一共有784个字段。可以数字将字段转化为图片，代码如下。

import matplotlib.pyplot as plt
def display_sample(num):

    image = mnist.data[num].reshape([28,28])
    plt.imshow(image, cmap=plt.get_cmap('gray_r'))
    plt.show()
display_sample(147)

输出结果如下。

2 模型创建与应用

该数据集已经是处理完毕后的结果，可以直接用来建模。首先是正常按照原来的思路进行模型创建与应用，这里采用逻辑回归模型。

（1）划分数据。一共有 7w 个，训练集合 6w ，测试集合 1w，test_size=1/7.0。

train_img, test_img, train_lbl, test_lbl = train_test_split(
    mnist.data, mnist.target, test_size=1/7.0, random_state=0)
print(train_img.shape)
print(test_img.shape)

输出结果如下。

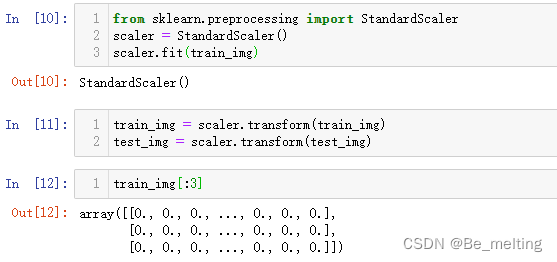
（2）数据转化。由于算法会使用距离计算，所以如果有数据特别大或特别突出 Ourlier，要么去掉异常数据，要么标准化。

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(train_img)
train_img = scaler.transform(train_img)
test_img = scaler.transform(test_img)
train_img[:3]

输出结果如下。

（3）模型创建与评估。采用逻辑回归模型进行建模，为了对比出采用PCA和不采用PCA的模使用到计时函数，代码如下。

from sklearn.linear_model import LogisticRegression
%%time
logisticRegr = LogisticRegression(solver = 'lbfgs')  
logisticRegr.fit(train_img, train_lbl)  
score = logisticRegr.score(test_img, test_lbl)  
print(score)

输出结果如下。此时模型的得分为0.9162，测试机器的运行时长为23.9s。

（4）PCA应用。记住未使用PCA时数据的维度，然后指定保留的特征占比，通过fit后就可以知道减少的字段数量，代码如下。

mnist.data.shape
from sklearn.decomposition import PCA
pca = PCA(0.95)
pca.fit(train_img)
pca.n_components_ 
train2_img = pca.transform(train_img) 
test2_img = pca.transform(test_img)
train2_img.shape
train_img.shape

输出结果如下。 PCA(0.95)是指经过PCA后保留95的特征，通过n_components_可以输出经过处理后当前的数据中保留的成分。对比原来的数据维度可以发现，只减少了5%的特征，但是数据的字段减少了一半以上的数量。

对于训练数据和测试数据一样是要经过转化，直接采用transofm即可，然后拿着处理完毕后的数据进行建模，查看模型得分已经运行时间，代码如下。

%%time
logisticRegr = LogisticRegression(solver = 'lbfgs')  
logisticRegr.fit(train2_img, train_lbl) 
score = logisticRegr.score(test2_img, test_lbl) 
print(score)

输出结果如下。此时模型的得分为0.9201，测试机器的运行时长为12.6s。

再次尝试把特征成分降到0.9，看一下数据字段减少数量，模型得分以及运行时间。

pca2 = PCA(.9) 
pca2.fit(train_img)
pca2.n_components_ 
train3_img = pca2.transform(train_img)  
test3_img = pca2.transform(test_img)
%%time
logisticRegr = LogisticRegression(solver = 'lbfgs')  
logisticRegr.fit(train3_img, train_lbl)  
score = logisticRegr.score(test3_img, test_lbl)  
print(score)

输出结果如下。此时数据的字段数量为234，只有原来数据的四分之一左右，而且此时模型的得分在0.9199，与原模型的得分还多，而且模型运行时间要比原模型缩减了一半以上的时间。

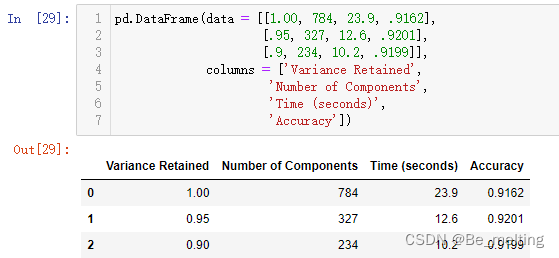
（5）多模型结果汇总。可以进一步将各个模型对应的结果构造成为DataFrame数据类型，方便绘图分析。

pd.DataFrame(data = [[1.00, 784, 23.9, .9162],   
                     [.95, 327, 12.6, .9201],     
                     [.9, 234, 10.2, .9199]], 
             columns = ['Variance Retained',
                      'Number of Components', 
                      'Time (seconds)',
                      'Accuracy'])

输出结果如下。