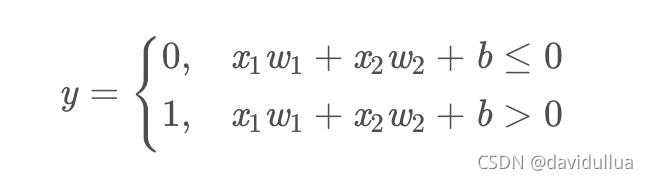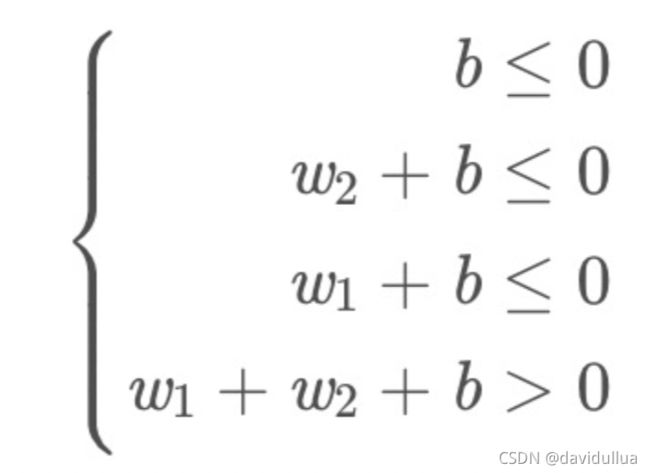深度学习代码实践(四)- 从0搭建一个神经网络:感知机与激活函数
参加过多次的神经网络的分享,都没弄明白
为什么神经网络能够工作,怎么样理解神经网络可以工作?
往往会得到这些答案:
神经网络很难解释为什么能够工作。
不用管他为什么能够工作,只要知道怎么用就好了。
到现在为止,还不能很好地解释神经网络为什么能够工作。
神经网络要解的根本问题
对于输入的多个变量(成百上千,甚至上万个变量),经过多次的函数变换,得到最终解。
机器学习的方法,通过人工找到样本的特征,建立模型进行预测。
而神经网络是自动找到样本的特征,建立模型进行预测。
典型的场景
输入图像的特征,识别图像是哪一种动物/植物(典型的分类问题);
输入一组特征,判断明天的天气,股票的涨跌(分类问题);
处理过程(机器学习的工作过程)
学习:输入的训练集进行学习(从已知结果/打过标签的对象和输入的特征进行学习)
预测/推理:对未知的对象,根据输入特征,自动做推理预测(打标签)
神经网络的本质:通过参数与激活函数来拟合特征与目标之间的真实函数关系。单层网络只能做线性分类任务,两层神经网络可以无限逼近任意连续函数。
例子: 手写数字的识别
训练数据: 60000张灰度图像(每个像素值范围:0-255),每张图像用一个 28x28 像素的矩阵表示,以及每张图像表示的是 0-9 中的哪一个数字。
要求解的问题
输入:一个 28x28 像素的灰度图像
输出:0-9 的数字
这个问题,要设计一个神经网络,用来处理输入,得到输出。
数学语言定义的需求
输入:28x28 维像素数组,即 784 个变量的输入 [x1, x2, x3, ... x784],
输出: 包含10个元素的向量 y = [z0, z1, z2, z3, z4, ...., z9] ,
每一个元素的值表示是这个索引值的概率。 zi 是表示这个输入的图像是数字 i 的概率。
比如:
y = [ 0.1, 0.04, 0.2, 0.6, 0, 0, 0, 0.01, 0.02, 0.03]
这个输出里面, z3 = 0.6, 数字3的概率是 0.6,认为识别的图像对应数字3.
用 t 来表示正确解,也用10个元素的向量表示, 如以下 t 表示数字3:
t = [0, 0, 0, 1, 0, 0, 0, 0, 0, 0,]
这里将正确解标记为1, 其他标签标记为0的表示方法,称为 one-hot 表示法。
神经网络的方法
神经网络:即人工神经网络的简称,使用感知机模拟类人脑神经网络结果的多层网络。
使用感知机模拟神经元,对输入信号做出反馈;使用多层感知机组成网络,模拟神经网络。
1986年,数学家 乔治塞班克(George Cybenko)证明了神经网络可以被看成一个通用逼近函数,一个隐藏层的神经网络可以逼近任意连续函数,两个隐藏层网络可以逼近任意函数。 后来被奥地利数学家科特霍尼可(Kurt Hornik)完善。
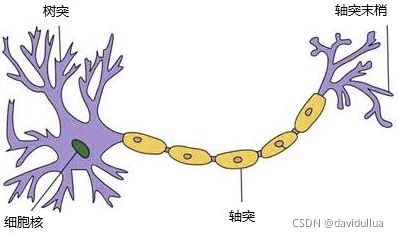
人脑的神经元
一个神经元通常具有多个树突,主要用来接受传入信息;而轴突只有一条,轴突尾端有许多轴突末梢可以给其他多个神经元传递信息。轴突末梢跟其他神经元的树突产生连接,从而传递信号。这个连接的位置在生物学上叫做“突触”。
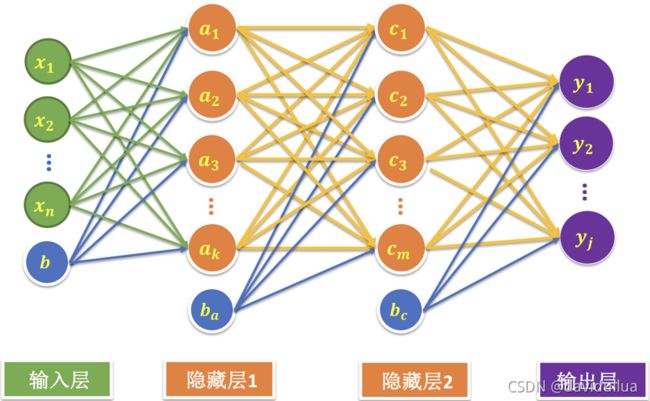
从输入层到隐藏层时,数据发生了空间变换。也就是说,两层神经网络中,隐藏层对原始的数据进行了一个空间变换,使其可以被线性分类,然后输出层的决策分界划出了一个线性分类分界线,对其进行分类。这样就导出了两层神经网络可以做非线性分类的关键--隐藏层。
矩阵和向量相乘,本质是对向量的坐标空间进行一个变换。因此,隐藏层的参数矩阵的作用就是使得数据的原始坐标空间从线性不可分,转换成了线性可分。
两层神经网络通过两层的线性模型模拟了数据内真实的非线性函数。
因此,多层的神经网络的本质就是复杂函数拟合。
神经网络能够解决的问题
回归
分类问题
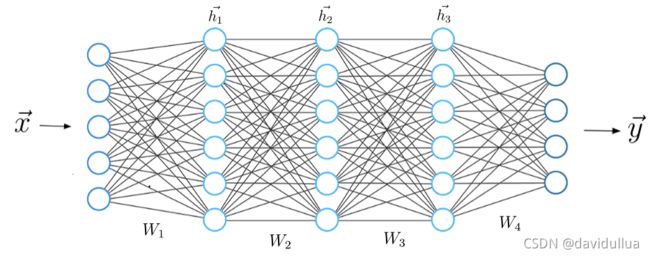
图:神经网络
如何构建神经网络?
从构建神经元开始,用来构建神经元的对象,称之为感知机。
接下来来看感知机。
感知机(Perceptron)
先讲结论:
1.感知机可以实现逻辑电路的运算(与门,与非门,或门)
2.多层感知机可以实现异或门
3.基础的逻辑门(与门,与非门,或门,异或门)可以表示加法器,进而可以构建计算机 (通过与非门和组合能够实现计算机,同理通过感知机也可以表示计算机)
4.基础的感知机可以表达线性分类器
感知机(perceptron),又称“人工神经元”或“朴素感知机”。
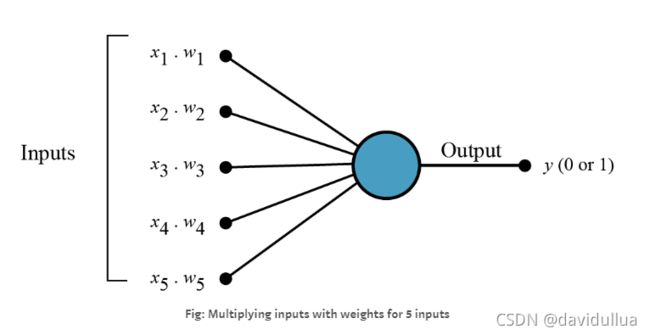
感知机接受多个输入信号,输出一个信号。感知机的信号只有“0(不传递信号)”和“1(传递信号)”两种。
逻辑门有4种:
AND
NOT AND
OR
XOR
用感知机(函数)表达与非门
一个简单感知机的函数定义
权重w1,w2表示各个输入的重要程度。偏置b表示神经元激活的难易程度,b越大则越易被激活。
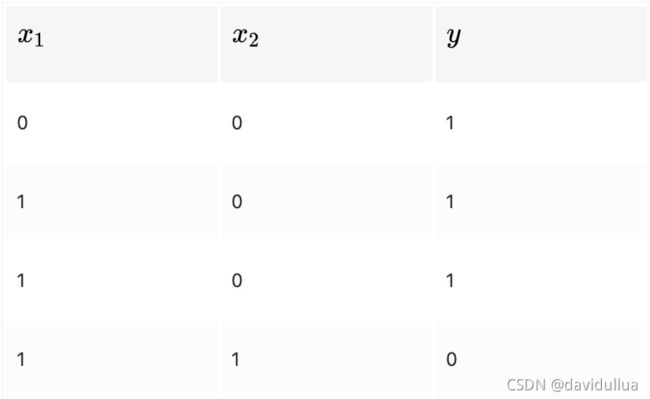
与门真值表 (AND Gate)
代入前面的函数, 有
满足这组关系的w1 , w2 , b很多,比如取 0.3,0.5,-0.7
与非门(NAND Gate)
要表示与非门,可以用(w1,w2,b)=(-0.3,-0.5,0.7)这样的组合(其他的组合也是无限存在)。实际上只要把实现与门的参数值的符号取反,就可以实现与非门。
感知机的局限性:
单层感知机只能表达与门 AND,与非门 NAND,或门 OR。不能表达异或门。
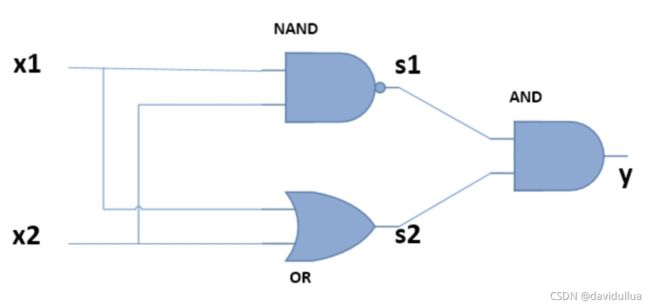
用两层感知机,可以表达异或门,如下:
Y = X1 XOR X2 = (X1 NAND X2) AND (X1 OR X2)
即异或门的逻辑是: NOT AND (X1, X2), 且 X1 OR X2 中的一个为真。
Code - 与门 & 或门 & 与非门 & 异或门的代码实现
import numpy as np
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b= -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))
def XOR(x1,x2):
s1 = NAND(x1,x2)
s2 = OR(x1,x2)
y = AND(s1,s2)
return y
使用与门 & 异或门 表达加法器
加法器(adder)是一种用于执行加法运算的数字电路部件,是构成电子计算机核心微处理器中算术逻辑单元的基础。
半加器:(half adder)的功能是将两个一位二进制数 A, B 相加。它有两个输出:
- 和:记作 S,来自对应的英语 Sum;
- 进位:记作 C,来自对应的英语 Carry一位的数字。
- 因此,这两个一位二进制数的和用十进制表示即等于2C + S。
- 上图是一个最简单的半加器设计,使用一个异或门来产生 S,一个与门来产生 C
S = A XOR B
C = A AND B
半加器的真值表
| 输入 |
输出 |
||
| A |
B |
C |
S |
| 0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
朴素感知机的缺陷
朴素感知机是用前面的线性函数表达的感知机
y = w*x + b
缺陷:只能表达线性可以分的问题
线性可分函数
线性可分: 可以用一个线性函数把两类样本分开,比如二维空间中的直线、三维空间中的平面以及高维空间中的线型函数。
所谓可分指可以没有误差地分开;
线性不可分:有部分样本用线性分类面划分时会产生分类误差的情况。
图 线性可分 与 线性不可分
激活函数与感知机
线性不可分问题,需要使用到非线性函数,做非线性的映射。在基础感知机上面增加一个非线性函数,即可用来解决非线性问题,这个非线性函数称之为激活函数(为什么叫激活函数? 激活了一个带有基础感知机的神经元,使得神经元可以做出非线性的反馈,进而可以表示任意的函数)
激活函数就是连接NN和感知机的桥梁。
结论:
两层感知机(含一层非线性激活函数如sigmoid)可以表示任意函数 (数学家已证明)。
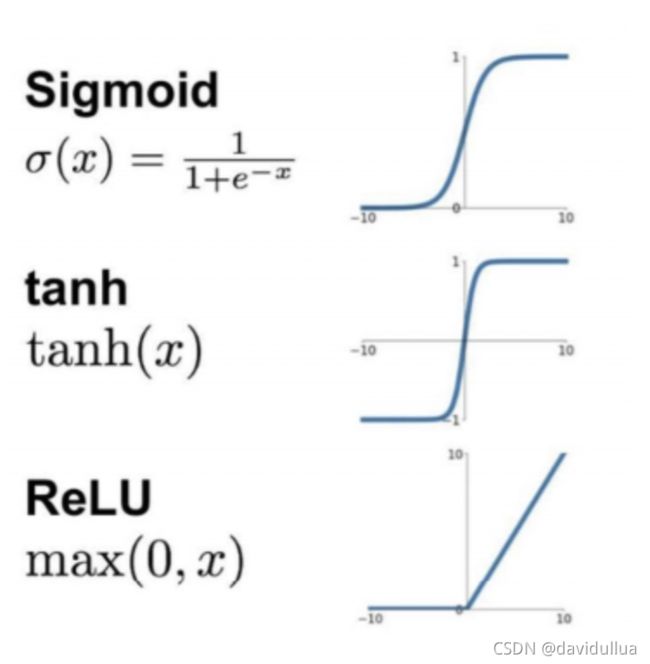
常用激活函数
Sigmoid 函数, tanh 函数, ReLU 函数(修正非线性单元)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def relu(x):
return np.maximum(0, x)研究发现,ReLU函数在训练多层神经网络时,更容易收敛,并且预测性能更好。
目前在深度学习中,最流行的非线性函数是ReLU函数。
ReLU函数不是传统的非线性函数,而是分段线性函数。
y=max(x,0) 在x大于0,输出就是输入,而在x小于0时,输出就保持为0。
这种函数的设计启发来自于生物神经元对于激励的线性响应,以及当低于某个阈值后就不再响应的模拟。
通用感知机
通用感知机是人工神经网络的基本结构(即神经元), 里面有两个基本运算:
1.计算输入向量的一个线性变换(x*w),对线性变换结果进行阈值判断(x*w + b),即仿射变换(Affine tansform) ;
2.非线性变换。
感知机的特性
感知机是具有输入和输出的算法。给定一个输入后,将输出一个既定的值。
感知机将权重和偏置设定为参数。
使用感知机可以表示与门和或门等逻辑电路。
异或门无法通过单层感知机来表示。
使用2层感知机可以表示异或门。
单层感知机只能表示线性空间,而多层感知机可以表示非线性空间。
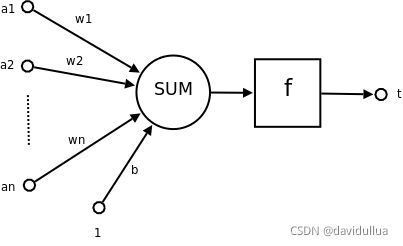
神经元的结构(带有激活函数的单一神经元)
- a1~an为输入向量的各个输入分量, x = [a1, a2, ..., an]
- w1~wn为神经元各个突触的权值, w = [w1, w2, ...., wn]
- b为偏置, 偏置的设置是为了正确分类样本,
- b是模型中一个重要的参数,即保证通过输入算出的输出值不能随便激活;
- f为激活函数,通常为非线性函数。
- t为神经元输出: t = f(X*W + b)
以 Sigmoid 作为激活函数的神经元
2层神经网络的结构
输入有256个节点(256维的输入变量),
在第一个隐藏层保持256个节点不变,第二个隐藏层放64个神经元。
隐藏层:神经网络内部的层,对外不可见,只在内部可见,称之为隐藏层。
定义各层的参数和偏置
每个神经元中都由一个仿射变换(x*w + b), 加上一个激活函数组成,
神经元以 ReLU 函数作为激活函数,每一层的结果表达:
tf.matmul 是矩阵相乘: y = x*w + b = tf.matmul(x, w) + b