数据挖掘学习——KNN(k-近邻)
1.数据在不同维度上分布的分类表现
以鸢尾花数集(Iris)为例。
Iris数据集如下(分别使用0、1、2表示山鸢尾、变色鸢尾和菖蒲锦葵):
(可以看到Iris数据集一共有4个维度特征)
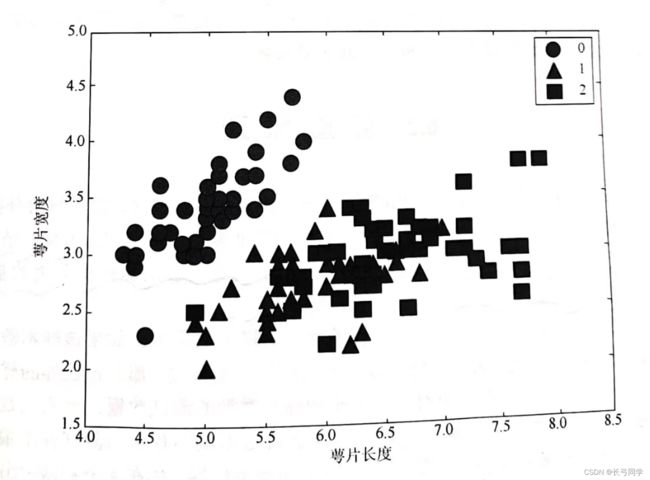
Iris数据中不同种类鸢尾花的萼片长度和萼片宽度的样本分布:
从图中可以发现,在萼片长度和萼片宽度这两个特征维度上,种类0与种类1、2有一定的辨识度,可以进行一个初步的分类,但是种类1和种类2仍旧无法分类。
现在我们将Iris数据集放到3个数据维度中去看:
可以看到此时三个种类出现了分层,此时我们可以对三个种类都进行分类。
这就是数据在不同维度上分布的分类表现。
2.KNN算法原理
KNN是一种基于实例的学习,没有很复杂的数学推理,其分类过程是直接建立在对数据集进行分类的基础上,因此也称为将所有计算推迟到分类之后的惰性学习算法。
分类算法流程如下:
(1)计算测试数据与训练数据特征值之间的距离
(2)对距离按照规则进行排序(递增)
(3)选取最近邻的k个数据进行分类决策(投票法)
(4)预测测试数据的分类
3.几种常见的距离计算方法
(1)欧几里得距离
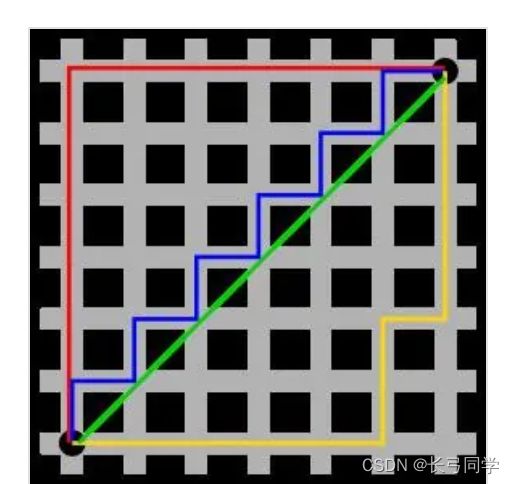
(2)曼哈顿距离(计程车几何)
(3)切比雪夫距离
(4)闵可夫斯基距离
4.kd树
kd树是对数据点所在的k维空间进行划分的一种数据结构,主要应用于多维空间的关键数据搜索,本质上是一种平衡二叉树。
在使用KNN算法对测试数据点进行分类时,需要计算测试数据点与训练样本集中每个数据点之间的距离,对距离进行排序,进而找出其中最近邻的k个样本数据。该方法的优势在于简单有效,但是当训练样本过大时,该方法的计算过程将比较耗时,为了提高KNN算法的搜索效率,减少距离计算的次数,通常采用k维(k-dimensional, kd)树方法。
5.KNN算法实战
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KDTree
from sklearn import datasets
from sklearn.model_selection import train_test_split
iris=datasets.load_iris()
data_train,data_test,target_train,target_test=train_test_split(iris.data,iris.target,test_size=0.3)
# 定义一个KNN分类器对象,n_neighbors为k值,algorithm是算法
knn=KNeighborsClassifier(n_neighbors=3,algorithm='kd_tree')
knn.fit(data_train,target_train)
# 把测试集的数据集传入即可得到模型的评分
score=knn.score(data_test,target_test)
# 预测给定样本数据对应的标签
predict=knn.predict([[0.1,0.2,0.3,0.4]])
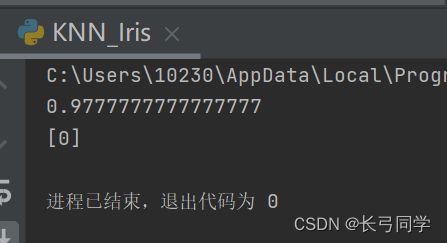
print(score)
print(predict)运行结果: