基于Spatial-Temporal Transformer的城市交通流预测

文章信息

本周阅读的论文是题目为《Spatial-Temporal Transformer Networks for Traffic Flow Forecasting》的一篇2021年发布在arXiv网站上的使用时空Transformer网络（STTNs）预测交通流的文章。

摘要

交通预测已成为智能交通系统的核心组成部分。然而，由于交通流的高度非线性特征和动态的时空依赖性，及时准确的交通预测，尤其是长时交通流预测仍然是一个开放性的挑战。在这篇文章中，作者提出了一种新的时空Transformer网络（STTNs）模型，该模型联合利用了动态有向的空间依赖性和长时依赖性来提高长时交通流预测的准确性。文章还提出了一种新的图神经网络，称为spatial transformer，利用自注意力机制对有向空间依赖性进行动态建模，以获取交通流的实时情况和交通流流向。模型在考虑相似性、连通性和协方差等因素的前提下，采用多头注意力机制对不同空间依赖模式进行联合建模。此外，temporal transformer被提出用于双向长时的时间依赖性的多步建模。与现有的模型相比，STTNs能够有效的对长期时空依赖性进行训练。实验结果表明，STTNs在真实数据集PeMS-Bay和PeMSD7(M)上具有竞争力，尤其是长期交通流预测方面。

介绍

交通预测中，某个节点的未来交通状态（如速度、流量和密度等）是根据其自身和邻近节点的历史交通数据来预测的，因此对于预测模型来说，有效地捕捉交通流地时空依赖性是非常重要的。交通流预测通常被分为短期（小于30分钟）和长期（大于30分钟）两个尺度。现有的预测方法例如时间序列模型和卡尔曼滤波等在短期预测中表现良好。然而，这些模型对时间序列数据的平稳假设在长期预测中并不实用，因为交通流本质上是高度动态的。另外，模型难以充分捕捉交通流中的时间和空间相关性用于长期预测。

交通网络可以表示为图结构，其中节点代表交通传感器，边代表相连节点间的权重，该权重由传感器间的欧式距离决定。因此，交通流可以视为随时间演变的图信号。近年来，图神经网络（GNNs）成为处理图数据的强大工具。空间或光谱图卷积网络被整合至基于卷积的序列学习模型或循环神经网络（RNNs）中以联合捕捉时间和空间的依赖性。然而，这些模型仍然受限于以下两个方面的原因，导致交通预测尤其是长时预测的精度不高：

固定的空间依赖性：在交通预测任务中，空间依赖性受道路拓扑结构、变化的交通流速度和多种因素（例如天气状况、高峰时段和交通事故等）的影响，具有高度动态性。对于每个传感器，与之相关的传感器是时刻变化的。图1(a)为交通预测中一个简单的例子，除了目标节点（紫色节点）的交通流速度外其他节点的交通流速度没有随时间发生变化。对目标节点而言，根据交通流速度和距离，考虑不同的相关节点（红色节点）来表示不同时刻下（t-1、t-2和t-3）的空间依赖性。考虑任意两个传感器之间的连通性和距离，其空间依赖性是复杂的，这是由于随时间变化的交通速度。不同方向（即上游和下游）的交通流空间依赖性也会不同。另外，如图1(b)所示，由于高峰时段周期性影响、天气条件变化影响以及交通事故意外发生的影响，空间依赖性随时间步长无规律地变化。因此，有必要捕捉节点间的动态空间依赖性以提高交通预测精度。

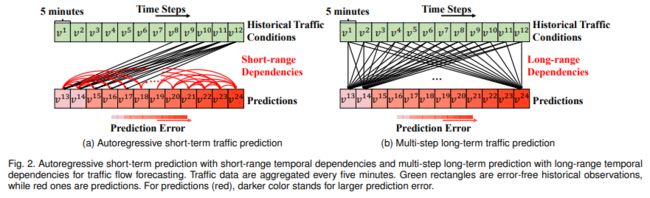
有限的时间依赖性：考虑不同时间步以及不同变化尺度的时间依赖性可以提升长时交通流预测的效果。图1(a)展示了不同时间步以及不同尺度下的空间依赖性，这意味着限制时间依赖性的范围尺度会降低预测性能。此外，如图2(a)所示，现有的自回归方法会导致长期交通预测中的预测误差不断累积传播。如图2(b)所示，通过从长距离但无误差的时间序列中提取长时时间依赖性以提高长期预测的精确性也许是可行的。

这篇文章中，作者提出了一个新的时空Transformer模型（STTNs）以解决上述交通流预测中的挑战，主要贡献如下：

1. 文章提出了一个时空模块来动态建模长期时空相关性；

2. 文章提出了一种GNNs网络的变体，称为spatial transformer，动态捕捉随时间变化的有向的空间依赖性和隐藏的交通流空间模式；

3. 文章设计了temporal transformer以使用长时时间依赖性实现交通流多步预测。

具体来说，spatial transformer基于实时的交通流速度、交通传感器连通性和距离以及交通流的方向动态建模有向的空间依赖性。从带有位置嵌入（positional embeddings）的时空特征中学习高维子空间以捕捉随时间变化的空间依赖性。为表示突然变化的交通流，使用多头注意力机制捕捉隐藏的长范围时间变化模式。该模型减小了预测误差的传播，允许并行计算以提高效率。为了验证模型的有效性，文章在两个真实世界的交通数据集上进行实验，分别是PeMSD7(M)和PEMS-BAY。实验结果表明，STTNs可以实现良好的预测效果，尤其是长时预测。

Proposed Model

1. Problem Formulation

文章定义了一个交通网络G=(V,E,A)，其中V表示节点集合，共有N个节点，每个节点代表一个交通传感器，E是节点边的集合，反映传感器间的物理连接 。A是一个根据传感器间的欧氏距离所构建的N*N的邻接矩阵。这篇文章，作者主要针对N个传感器在t个时间步下的速度v进行预测，至于交通流量和密度都可以以相同方式计算。

Problem Statement (Traffic Forecasting)：给定过去M个时间段由N个传感器观测到的交通流状态和交通图网络G，学习交通预测模型F以预测未来T个时间步的交通流状态。

为实现精确预测，模型F从历史M个时间段的交通流状态和交通图网络G中捕捉动态空间依赖性和长时时间依赖性。然而，目前存在的方法无法应用于长时预测，因为它们仅仅考虑了固定的时空依赖性和短时时间依赖性。这篇文章提出了spatial transformer捕捉随时间变化的空间依赖性以动态训练预测模型F。另外长时时间依赖性可以有效的从基于多头注意力机制的temporal transformer中学习得到。

2. Overall Architecture

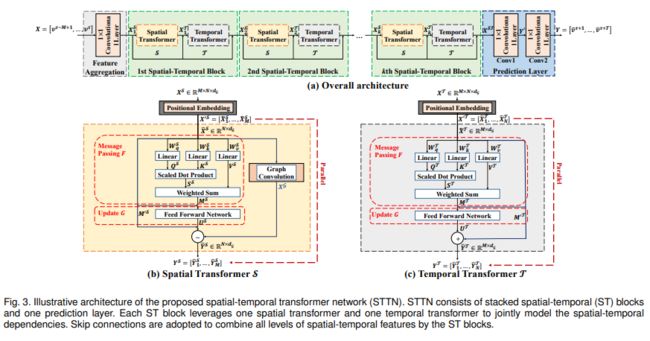
如图三所示，提出的时空transformer网络由堆叠的时空模块和一个预测层组成。每个时空模块由一个spatial transformer和一个temporal transformer构成以联合提取时空特征。时空模块可以进一步堆叠形成深度模型便于捕捉深度时空特征。另外，预测层使用两个单位卷积层以聚合这些时空特征用于交通预测。

Spatial-temporal Blocks：某个节点未来的交通流状态由其邻接节点的交通流状态、观测时间步、交通意外和天气情况等共同决定。文章提出了时空模块以整合spatial transformer 和temporal transformer便于联合建模交通网络中的空间和时间特性。第l个时空模块的输入是一个3D张量，表示M个时间步下N个节点的维特征，由l-1个时空模块所提取。Spatial transformer S和Temporal transformer T堆叠到一起以生成3D的输出张量。在第l个时空模块，spatial transformer S从输入节点特征和邻接矩阵A提取了空间特征。

和整合至一起以生成输入至temporal transformer。

至此模型获得的输出张量，并将其输入到第l+1个时空模块。根据任务不同，可以通过叠加多个时空块来提高模型的预测性能。

Prediction Layer: 预测层基于最后一个时空模块提取的时空特征，利用两个卷积层实现多步预测。其输入是一个2D张量，表示过去t个时间段内N个节点维时空特征。关于N个节点未来T个交通流情况的多步预测被定义为：

3. Spatial Transform

如图三（b）所示，spatial transformer由时空位置嵌入层、固定图卷积层、动态图卷积层和门控机制组成以便于信息融合。时空位置嵌入层整合了每个节点时空位置信息（拓扑信息、连通性、时间步）。一段时间内的交通信号可以被分解为由道路拓扑决定的平稳成分（传感器的连通性和距离）和由实时交通状态和突发事件决定的动态成分。因此，文章提出了一个固定图卷积层和一个动态图卷积层以分别捕捉空间依赖性中平稳和有向动态的部分，提出的spatial transformer可以视为一个用于动态图构建和特征学习的基于信息传递的图神经网络。

Spatial-temporal positional embedding：图1(a)表明了图网络中两个节点的空间依赖性用节点间的距离和观察时间步长决定。Transformer无法捕捉由前向全连接架构观察到的空间和时间信息。因此，先前位置嵌入被要求将位置信息嵌入到输入序列。在提出的spatial transformer中，采用可学习的时空位置嵌入层学习每个节点特征的时空嵌入。字典和分别作为空间和时间位置嵌入矩阵。使用是图邻接矩阵初始化，考虑了节点间连通性和距离以建模空间依赖性；而根据one-hot时间编码初始化，将时间步嵌入到每个节点。最终使用单位卷积整合获得嵌入特征，并将其输入到静态和动态图卷积层以学习空间特征。

Fixed graph convolutional layer：图卷积是将经典的基于网格的卷积推广到图域。基于学习到的权值和预定义的图，通过聚合相邻节点的信息来获得节点特征。本节采用基于Chebyshev多项式近似的图卷积方法学习结构感知的节点特征，从而从道路拓扑中获取平稳的空间依赖性。文章定义D为图G的度矩阵，其中对角元素。归一化拉普拉斯矩阵L定义为，缩放拉普拉斯矩阵定义为，其中是L中最大的特征值。给定嵌入特征，结构感知节点特征可以由基于切比雪夫多项式的K阶图卷积网络获得。

其中是的第j行（通道），表示可学习权重。由于图网络G是基于传感器间的物理连通性和距离所构建，由拓扑结构所决定的平稳空间依赖性可以通过静态图卷积网络深入挖掘。

Dynamical graph convolutional layer：为了捕捉随时间演变的隐藏的空间依赖性，文章提出了一种新的动态图卷积层便于在高维度子空间训练和建模。具体而言，模型学习了特征的线性映射，将每个节点的输入特征投影到高维度子空间内。如图4所示，自注意力机制被用于根据图信号变化来有效建模节点间的动态空间依赖性。由于预定义的道路拓扑结构无法充分表示交通网络的动态空间依赖性，因此模型使用多层线性映射在不同子空间建模受多种因素影响的动态有向空间依赖性。

每个时间步的嵌入特征矩阵首先通过前向神经网络投影至高维度子空间中，具体如下：

接着使用注意力机制学习节点的空间依赖性，其实现与大部分注意力机制模型相同，具体如下：

值得注意的是，多种模式的空间依赖性可以通过多头注意力机制学习捕捉，在不同子空间建模隐藏空间依赖性。此外，在每个节点上应用一种具有非线性激活函数的共享的三层前馈神经网络，进一步改善了基于学习到的节点特征的预测，并探索了特征通道之间的相互作用，以更新。

其中表示残差链接，其目的是为了训练的稳定。将和相加输入到门控机制以实现特征融合。

Gate mechanism for feature fusion：模型提出门控机制便于融合由静态和动态图卷积层学习到的空间特征。门控机制通过线性投影和sigmoid激活函数融合了由两个卷积层分别学习到的空间特征。

General dynamical graph neural networks：目前大部分图卷积网络依赖于预定义的图拓扑结构，无法适应输入的图信号。文章阐述了spatial transformer可以被视为一个信息传递的迭代特征学习过程，即动态图卷积网络以更新所有节点。定义节点v的输入特征为，对于任意节点v，它可以接收到来自节点集合V的信息。其中F表示信息传递公式，此处为注意力机制。

在spatial transformer中，G表示共享位置信息的前向神经网络，即为上述提到的三层前馈神经网络。与一般的图卷积网络对比，spatial transformer可以视为一个通用的消息传递动态图神经网络。

4. Temporal transformer

图3(c)为文章提出的temporal transformer结构，其目的在于有效捕捉长范围时间依赖性。与RNN和其变体模型相比较，temporal transformer很容易通过并行计算拓展到长序列处理中以捕捉长范围的时间依赖性。由于temporal transformer与spatial transformer的结构相似，此处不再展开描述，读者可自行阅读原文查阅细节。至此模型结构部分讲解完毕，接下来将简单介绍实验部分。

实验

文章在两个真实世界数据集PeMSD7(M)和PEMS-BAY上对模型的预测效果进行实验验证。另外，还对模型结构进行了消融实验验证多步预测以及spatial transformer和temporal transformer对于长时预测的有效性。

(1) Dataset and Data Preprocessing

PeMSD(M)：包含加利福尼亚州高速公路上228个传感器在2012年五月到六月份工作日的交通流速度数据。

PEMS-BAY：包含加利福尼亚湾区内325个传感器在2017年1月1日到五月31日六个月内的交通数据。

交通流速度数据按每5分钟整合统计，并根据Z-Score对数据进行归一化以作为输入。道路的拓扑信息通过图邻接矩阵表示。PeMS-BAY数据集的图被提前定义为一个有向图以区别不同车流方向的影响。实际上，用一个合适的度量来表示不同车辆方向的影响是很难构造有向图的。本文利用自注意机制以数据驱动的方式对有向空间依赖进行建模，减轻了区分车流方向影响的计算负担。只需要无向图邻接矩阵来表示传感器之间的距离和连通性。在PEMS-BAY中，通过从每对节点的两个方向(即上游和下游)中选择较大的权值来生成道路拓扑的无向图。在PeMSD7中，邻接矩阵是基于传感器之间的距离对称的。

(2) Evaluation Metrics and Baslines

文章根据MAE、MAPE和RMSE来评估STTN和其他基线模型的预测性能。基线模型包括历史平均（HA）、带有卡尔曼滤波的自回归综合移动平均（ARIMA）、线性支持向量机（LSVR）、前向神经网络（FNN）、FC-LSTM、STGCN、DCRNN以及Graph WaveNet。

对于PeMSD7(M)，采用一个时空块。每个具有64个特征通道的spatial transformer和temporal transformer采用2个隐藏层和1个自注意力层。考虑到数据集PeMS-BAY在空间和时间尺度上比PeMSD7(M)大得多，在PeMS-BAY数据集上，模型将三个时空块叠加在一起，对时空相关性进行建模。在每个时空块中，每个spatial transformer和temporal transformer分别由一个隐藏层和单个注意力层组成，共有64个特征通道。

(3) Experiment Results

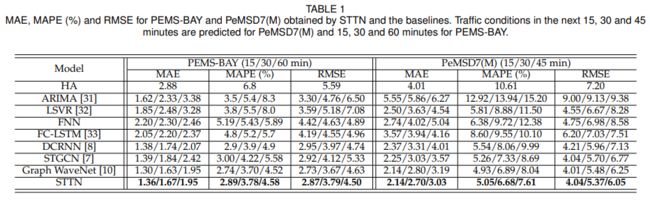
表1为STTN和其他基线模型在两个数据集上不同预测时段长度下的预测效果指标。可以看出在PeMSD7(M)数据集上，STTN随着预测时段长度增大，预测效果优势更加明显，表明联合考虑动态空间依赖性和长期时间依赖性可以提高长时预测的效果。在PEMS-BAY数据集上，STTN表现也是由于其他基线模型。Graph WaveNet和DCRNN采用了基于非对称邻接矩阵的双向扩散图卷积以明确考虑车流方向的影响。STTN利用自注意力机制学习对称邻接矩阵中动态有向的空间依赖性。另外，STTN通过时空模块的堆叠，深度学习建模时空依赖性。

文章进一步评估STNN、Graph WaveNet、STGCN和DCRNN一天时段的交通预测。图5表明，与STGCN和DCRNN相比，STTN和Graph WaveNet改进了交通流变化区域的预测效果，例如在步长为[60, 84]范围。需要注意的是，STGCN和DCRNN的预测曲线存在明显的时移，这表明预测误差随着时间步长而增大，尤其是在变化剧烈的区域。另外，STTN可以捕捉长步长内的连续变化，例如步长为[84, 192]的区域，这表明由STTN捕捉到的动态空间依赖性和长时时间依赖性有利于交通预测，尤其是长时预测。

(4) Computational Complexity

文章评估了DCRNN、STGCN、Graph WaveNet和STTN的计算费用。所有的实验均在同一个GPU上进行。表2统计了各模型每次迭代的平均训练速度。STGCN因为其完全卷积结构，因此训练费用较小；DCRNN的训练时间较长，这是由于模型的循环结构所致。STTN与Graph WaveNet和DCRNN相比，计算费用分别降低10-40%和40-60%，表明STTN可以在不需要过多计算费用的前提下实现长期预测。

(5) Ablation Studies

Multi-step prediction vs. Autoregressive prediction

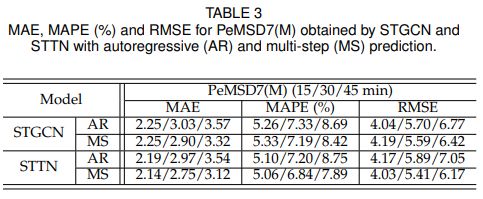
交通流预测中，自回归预测是一种流行的预测方法，它利用对每个时间步的预测来进行后续的预测。然而自回归预测由于逐步预测的误差累积导致预测误差，不适用于长时预测。DCRNN提出采样方案来解决这个问题，本文则明确利用历史观测数据进行长期多步预测，而不是基于观测值。为了合理验证，文章比较仅有一个时空模块的STGCN和STTN在自回归或多步预测情况下的预测效果。表3表明在自回归情况下，STTN与STGCN相比，在MAE、MAPE和RMSE中均有显著的增益。需要注意的是，与其他模型相比，STTN在长期预测中的预测误差增长缓慢。

Effectiveness of spatial transformer

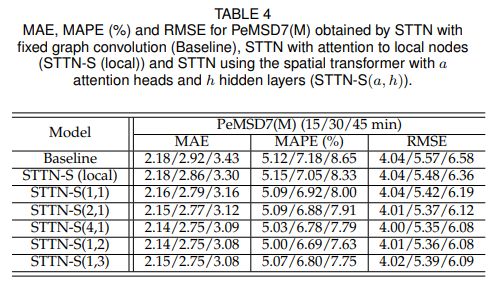
文章证明了提出的spatial transformer可以建模动态空间依赖性，以提高长期预测的性能。STTN的变体被考虑用来评估模型建模空间依赖性的效果。基准模型由一个静态图卷积层和一个在STGCN中采用的基于卷积操作的序列建模模型(GLU)组成。STTN-S(local)是一种基于注意力机制的方法，通过屏蔽学习到的动态依赖矩阵将注意力限制目标节点的k近邻节点。STTN- S(a, h)表示使用了spatial transformer的STTN，其中spatial transformer带有a个注意头和h个隐藏层。因此，基线模型仅仅建模固定的空间依赖性，而STTN-S(local)和STTN- S(a, h)分别考虑局部和全局动态空间依赖性。

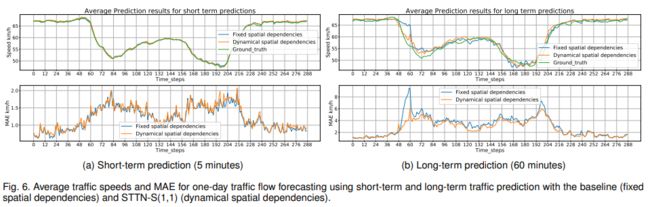
表4显示，STTN-S(1,1)在很大程度上优于基线模型，尤其是在长期预测方面，这意味着spatial transformer可以利用动态空间相关性来实现精确的长期预测。图6展示了基线模型和STTN-S(1,1)在测试集上短期（5分钟）和长期（60分钟）预测一天交通流的平均结果。STTN-S(1,1)在长期预测方面取得了更好的预测效果，尤其是在突然变化的区域，例如图6(b)中步长为[48, 84]的范围。文章进一步评估了捕捉局部和全局空间相关性的spatial transformer。根据表4，带有局部约束的STTN-S(local)不如带有spatial transformer 的STTN，这表明全局动态空间依赖性可以促进交通流预测。另外，文章同样比较了STTN-S(local)和STTN-S(1,1)的可学习空间依赖性。图7(c)表明STTN-S(local)在一个局部邻接范围内联系传感器，而STTN-S(1,1)随着时间步长的增加空间依赖性增加，这是由于大多数相邻传感器间的距离很小。

此外，表4统计了在spatial transformer中不同注意头数和隐层下得到MAE、MAPE和RMSE。随着注意头的增加，交通流预测性能不断提高，因为多头注意可以在不同的潜在子空间中建模空间依赖，从而进一步利用依赖性的隐藏模式。相反，隐藏层的数量增多对预测性能影响不大，这意味着一个隐藏层足以捕获PeMSD7(M)的空间相关性。

Effectiveness of Temporal Transformer

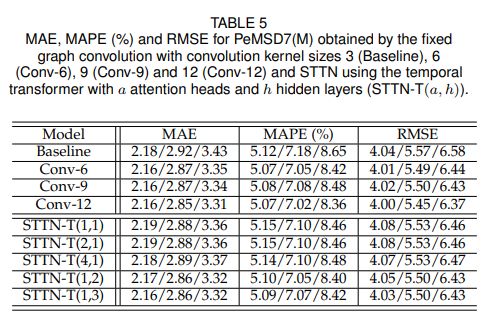
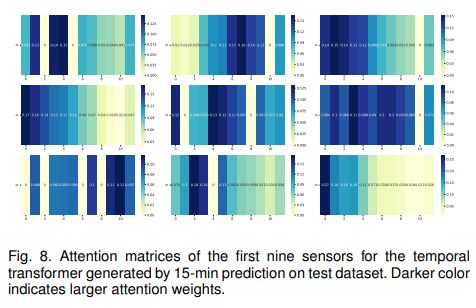
文章进一步验证，提出的Temporal Transformer是有效的，以获取长期的时间相关性，准确的交通流预测。文章采用与验证spatial transformer实验中一致的基准模型，其中调整了GLU层中的卷积核大小以控制时间依赖性的范围，卷积核的大小分别设置为6(Conv-6), 9(Conv-9)和12(Conv-12)。表5表明，随着卷积核大小的增大，可以捕捉到范围更大的时间依赖性，从而提高长时预测的效果性能。因此，文章用提出的temporal transformer替换GLU层来验证其有效性。由表5可以发现，在长期预测中，temporal transformer由于固定的图卷积。图8为前9个传感器在temporal transformer中的注意矩阵，可以看出不同传感器的时间注意权重不同。在某些情况下，最早时间步的依赖性被应用于多步预测。

对于temporal transformer中多头的数量和隐藏层的数量，文章也进行了研究。图5表明多头注意力不会提高交通预测的效果，因为时间依赖性不如空间依赖性复杂。另外，随着隐藏层数量的增加，交通预测效果提高。

结论

该文章提出了一种新的spatial-temporal transformer模型，以改善交通流的长期预测。它可以动态建模各种规模的空间依赖关系，以及捕获长期的时间依赖关系。在两个真实数据集上的实验结果表明，本文提出的STTN具有良好的性能，尤其是在长期预测方面。此外，提出的spatial transformer可以推广到动态图特征学习的各种应用。

Attention

欢迎关注微信公众号《当交通遇上机器学习》！如果你和我一样是轨道交通、道路交通、城市规划相关领域的，也可以加微信：Dr_JinleiZhang，备注“进群”，加入交通大数据交流群！希望我们共同进步！