【刷题日记】二叉树经典进阶题目
大家好,我是白晨,一个不是很能熬夜,但是也想日更的人✈。如果喜欢这篇文章,点个赞,关注一下白晨吧!你的支持就是我最大的动力!
文章目录
- 前言
- 二叉树进阶题目
-
- 1.根据二叉树创建字符串
- ☄2.二叉树的层序遍历
- 3.二叉树的层序遍历 II
- 4.二叉树的最近公共祖先
- 5.二叉搜索树与双向链表
- 6.从前序与中序遍历序列构造二叉树
- 7.从中序与后序遍历序列构造二叉树
- ☂8.二叉树的前序遍历(非递归)
- ☔9.二叉树的中序遍历(非递归)
- ⛱10.二叉树的后序遍历(非递归)
- 后记
前言
虽然还有很多课,但是也不能忘了写编程题呀。
本次白晨为大家总结了二叉树的经典进阶题目,需要一定的二叉树的基础,如果没有了解过二叉树的同学可以先读【数据结构】二叉树全解析(入门篇)了解一下二叉树这种十分经典的数据结构。这次白晨总结的题目都是互联网大厂必考的二叉树题目,也是思想非常经典的题目,第一次做可能想不到这样的思路,但是当见得多了就自然而然有这样的思路了,在做题中就是锻炼这种思路的过程。
都是很有代表性的经典题目,适合大家复习和积累经验。
大家可以自己先试着自己挑战一下,再来看解析哟!
二叉树进阶题目
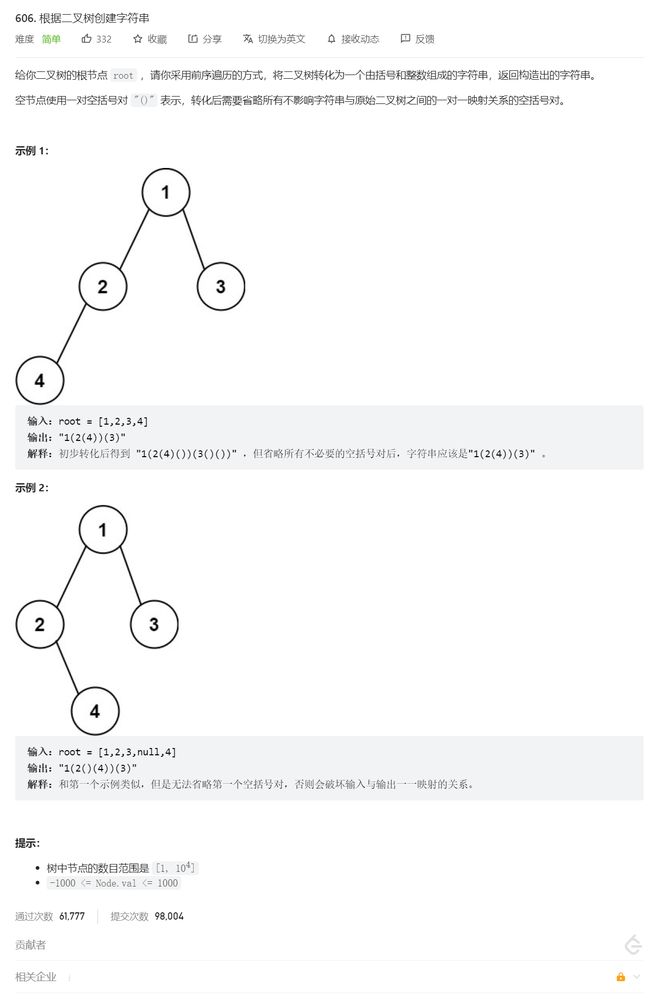
1.根据二叉树创建字符串
原题链接:根据二叉树创建字符串
算法思想:
-
打眼一看就应该是前序遍历得到的字符串,但是为了将树的层次分清楚(也就是带括号),需要对前序遍历进行一定的控制。
-
什么叫不影响字符串与原始二叉树之间的一对一映射关系的空括号对呢?
其实就是一个结点有左子树但是没有右子树,不需要再用一个空括号去表示右空树,可以直接省略这个括号。但是如果一个结点有右子树但是没有左子树,则不能省略左空树的括号,不然会导致左右子树无法分辨的问题。
具体实例可以见力扣题目的例题,展示的很详细。
-
前序遍历思路:
- 如果根结点为空,则直接返回。
- 将根结点的值转换为字符串加入结果字符串。
- 结点的左子树和右子树只要有一个不为空,说明需要在根节点值的后面加括号(左子树不为空,则需要加括号遍历;右子树不为空前面必须加上括号保证不会出现无法分辨的问题),并且遍历左子树。
- 如果右子树存在,加括号遍历右子树。
代码实现:
class Solution {
public:
void _tree2str(TreeNode* root, string& s) {
if (root == nullptr)
return;
s += to_string(root->val);
// 只要左右结点有一个为真,就遍历左子树
if (root->left || root->right)
{
s += '(';
_tree2str(root->left, s);
s += ')';
}
// 右子树为真,遍历右子树
if (root->right)
{
s += '(';
_tree2str(root->right, s);
s += ')';
}
}
string tree2str(TreeNode* root) {
string s;
_tree2str(root, s);
return s;
}
};
- 还有一种写法,思路与上面类似,只是代码看着简洁了很多。
class Solution {
public:
string tree2str(TreeNode* root) {
// root为空,返回空字符串
if (root == nullptr)
return "";
// 当左右都为空,说明是叶子结点,直接返回结点值的字符串,不用任何括号
if (root->left == nullptr && root->right == nullptr)
return to_string(root->val);
// 当左子树不为空,右子树为空,只用加一对括号,遍历左子树
if (root->left && root->right == nullptr)
return to_string(root->val) + '(' + tree2str(root->left) + ')';
// 一般情况,左右都不为空,分别遍历左右子树
return to_string(root->val) + '(' + tree2str(root->left) + ")(" + tree2str(root->right) + ')';
}
};
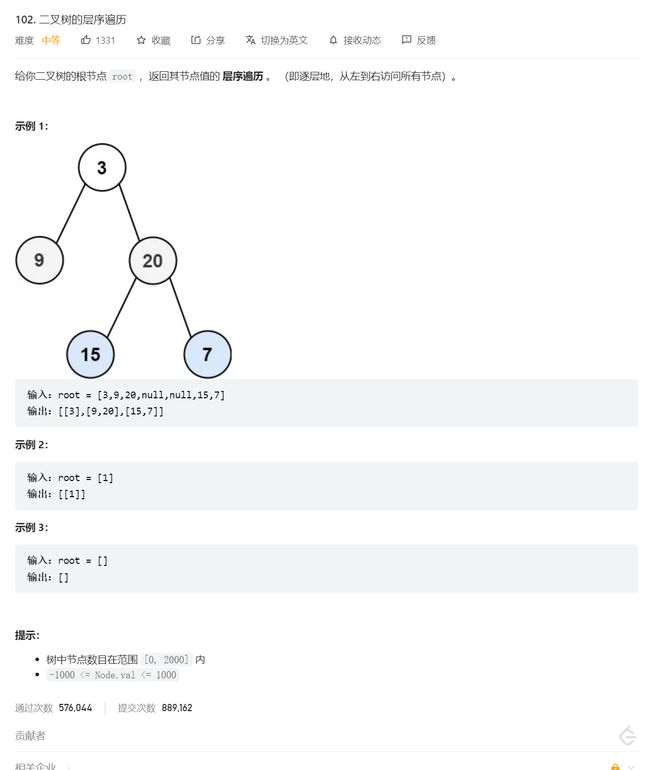
☄2.二叉树的层序遍历
原题链接:二叉树的层序遍历
算法思想:
- 就是一个很经典的层序遍历问题,没有了解过层序遍历的同学可以先看【数据结构】二叉树全解析(入门篇)了解一下层序遍历呀。
- 这道题就是要求按层输出,所以我们只要记录每一层的结点数量,然后每层遍历完以后换行就行。
代码实现:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;// 存放按层排列的二叉树层序遍历的结点
if (root == nullptr)
return vv;
queue<TreeNode*> q;// 队列用来层序遍历
q.push(root);// 将根入队
int num = 1;// 记录每一层的节点个数,第一层为1
vector<int> v;// 记录一层的输出
// 当队中不为空,继续循环
while (!q.empty())
{
TreeNode* cur = q.front();
q.pop();
num--;// 一层剩余结点数-1
v.push_back(cur->val);// 存放数据
if (cur->left)
q.push(cur->left);
if (cur->right)
q.push(cur->right);
// 当一层没有结点了,说明这一层遍历完了,准备进行下一层的遍历
if (num == 0)
{
vv.push_back(v);// 将这一层的数据记录
v.clear();// 清空v
num = q.size();// 此时队列的长度就是下一层结点的数量
}
}
return vv;
}
};
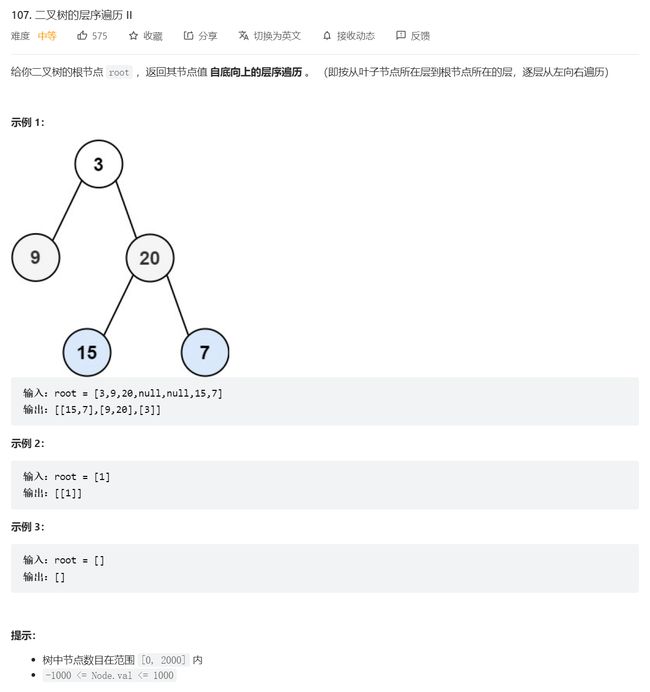
3.二叉树的层序遍历 II
原题链接:二叉树的层序遍历 II
算法思想:
- 比之上一题,这一题就是倒着进行层序遍历。
- 我们的思路就是正着遍历一遍,然后将结果逆置即可。
代码实现:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> vv;
if (root == nullptr)
return vv;
queue<TreeNode*> q;
q.push(root);
int num = 1;
vector<int> v;
while (!q.empty())
{
TreeNode* cur = q.front();
q.pop();
num--;
v.push_back(cur->val);
if (cur->left)
q.push(cur->left);
if (cur->right)
q.push(cur->right);
if (num == 0)
{
vv.push_back(v);
v.clear();
num = q.size();
}
}
// 结果逆置
reverse(vv.begin(), vv.end());
return vv;
}
};
4.二叉树的最近公共祖先
原题链接:二叉树的最近公共祖先
- 法一:查找左右子树法
算法思想:
-
何为最近公共祖先?
如果不算自己就是祖先的情况,那么我们可以定义:
p,q公共祖先结点就是如果一个结点n可以在左子树可以找到结点p (q),在右子树找到结点q (p),那么这个结点n就是最近公共祖先结点。
我们将定义拓展,
- 如果一个结点
n本身就是题目给出的结点p (q),并且在其子树中找到另一个结点q (p),那么这个结点也算是p,q最近公共的祖先结点。
那么,有没有可能同时出现两个满足上面条件之一的结点呢?
答案是不可能,大家可以自行去验证。
所以,我们可以唯一找到一个符合上面条件之一的结点。
-
根据上面的分析,我们可以得到一种方法:
- 根据前序遍历,依次查找遍历到的结点的左右子树是否为有
p,q结点。 - 如果
p,q结点分别在此结点的左右(右左)子树,此节点就是公共祖先结点,返回此结点。 - 如果
p,q结点都在此结点的左(右)子树,这个结点是这两个结点的祖先结点,但不是最近的,需要继续向这个结点左(右)孩子结点继续查找,直到发现p,q结点在不同的子树上。 - 如果
p,q结点为当前查找的结点,根据前序遍历,根节点先被访问,根据题意,必有最近公共祖先结点。所以,p,q先被访问的结点就是最近公共祖先结点。eg.leetcode示例二
- 根据前序遍历,依次查找遍历到的结点的左右子树是否为有
代码实现:
class Solution {
public:
// 查找函数
bool Find(TreeNode* root, TreeNode* x)
{
if (root == nullptr)
return false;
if (root == x)
return true;
return Find(root->right, x) || Find(root->left, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 遍历到空节点,返回空
if (root == nullptr)
return nullptr;
// 遍历到p结点,所以最近公共祖先就是p
if (root == p)
return p;
// 遍历到q结点,所以最近公共祖先就是q
else if (root == q)
return q;
// 查找此节点的左右子树
bool pInLeft = Find(root->left, p), pInRight = !pInLeft;
bool qInLeft = Find(root->left, q), qInRight = !qInLeft;
// 当p,q分别在不同子树时,此节点就是最近公共祖先
if ((pInLeft && qInRight) || (pInRight && qInLeft))
return root;
// 当p,q在同一棵子树时,向着子树方向继续找
else if (pInRight && qInRight)
return lowestCommonAncestor(root->right, p, q);
else if (pInLeft && qInLeft)
return lowestCommonAncestor(root->left, p, q);
// p,q不在此节点的左右子树
else
return nullptr;
}
};
- 法二:保存路径法
算法思想:
- 上一个方法思路简单,但是时间复杂度为 O ( N 2 ) O(N^2) O(N2),比较高,因为我们对于
p,q结点重复查找了很多次,浪费了时间,所以我们可以将其优化。 - 在查找
p,q结点时,将其从根结点到p,q结点的路径进行记录,最后再比较路径,找出最近的公共结点即可。
代码实现:
class Solution {
public:
// 查找并保存路径
bool FindAndRecord(TreeNode* root, TreeNode* x, stack<TreeNode*>& st)
{
if (root == nullptr)
return false;
// 入栈根节点
st.push(root);
// 前序查找
if (root == x)
return true;
if (FindAndRecord(root->left, x, st))
return true;
if (FindAndRecord(root->right, x, st))
return true;
// 找不到,出栈根节点
st.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr)
return nullptr;
stack<TreeNode*> stp, stq;
FindAndRecord(root, p, stp);
FindAndRecord(root, q, stq);
// 结点高度深的先走
while (stp.size() != stq.size())
{
if (stp.size() > stq.size())
stp.pop();
else
stq.pop();
}
// 当两个栈大小相同时,开始同时出栈,直到找到相同结点
while (stp.top() != stq.top())
{
stp.pop();
stq.pop();
}
return stp.top();
}
};
- 法三:后序查找
算法思想:
- 第一种方法前序遍历浪费了大量时间去重复查找,利用后序遍历就可以解决重复查找的问题。
- 优先查找根节点的左子树和右子树:
- 如果查找左右子树的返回结果都不为空,这就说明此节点就是最近公共祖先结点,返回根节点。
- 如果查找左子树的返回结果为空,说明两个结点都在右子树中,由于是后序遍历,从底到顶,如果发现了最近公共祖先结点,返回的就是最近公共祖先结点,所以,右子树的查找返回值就是最近公共祖先结点,返回右子树的查找结点即可。
- 如果查找右子树的返回结果为空,说明两个结点都在右子树中,由于是后序遍历,从底到顶,如果发现了最近公共祖先结点,返回的就是最近公共祖先结点,所以,左子树的查找返回值就是最近公共祖先结点,返回左子树的查找结点即可。
代码实现:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 如果结点为空,为目标结点,直接返回根节点即可
if (root == nullptr || root == p || root == q)
return root;
TreeNode* lson = lowestCommonAncestor(root->left, p, q);
TreeNode* rson = lowestCommonAncestor(root->right, p, q);
if (lson == nullptr)
return rson;
if (rson == nullptr)
return lson;
return root;
}
};
5.二叉搜索树与双向链表
原题链接:二叉搜索树与双向链表
算法思想:
- 这道题如果硬解非常吃力,所以,我们需要引入一些辅助结点记录中序遍历的前驱结点,方便改变结点的链接关系。
- 这道题主要就是改变结点链接关系,具体实现见代码。
代码实现:
- 引用记录前驱结点
class Solution {
public:
// 用引用不断改变前驱结点
void InOrderConnect(TreeNode* cur, TreeNode*& prev)
{
if (cur == nullptr)
return;
InOrderConnect(cur->left, prev);
// 如果前驱结点不为空,前驱结点的后继节点就是当前结点
// 前驱结点为空:中序遍历的第一个结点的前驱就为空
if (prev)
prev->right = cur;
// 当前结点的前驱结点就是prev
cur->left = prev;
// 跟新前驱节点
prev = cur;
InOrderConnect(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if (pRootOfTree == nullptr)
return nullptr;
TreeNode* prev = nullptr;
TreeNode* head = pRootOfTree;
InOrderConnect(pRootOfTree, prev);
// 找头节点
while (head->left)
head = head->left;
return head;
}
};
- 全局变量记录前驱结点
class Solution {
public:
TreeNode* head = nullptr;
TreeNode* prev = nullptr;
TreeNode* Convert(TreeNode* pRootOfTree) {
if (pRootOfTree == nullptr)
return nullptr;
Convert(pRootOfTree->left);
// 顺便记录头节点
if (head == nullptr)
head = prev = pRootOfTree;
else
{
prev->right = pRootOfTree;
pRootOfTree->left = prev;
prev = pRootOfTree;
}
Convert(pRootOfTree->right);
return head;
}
};
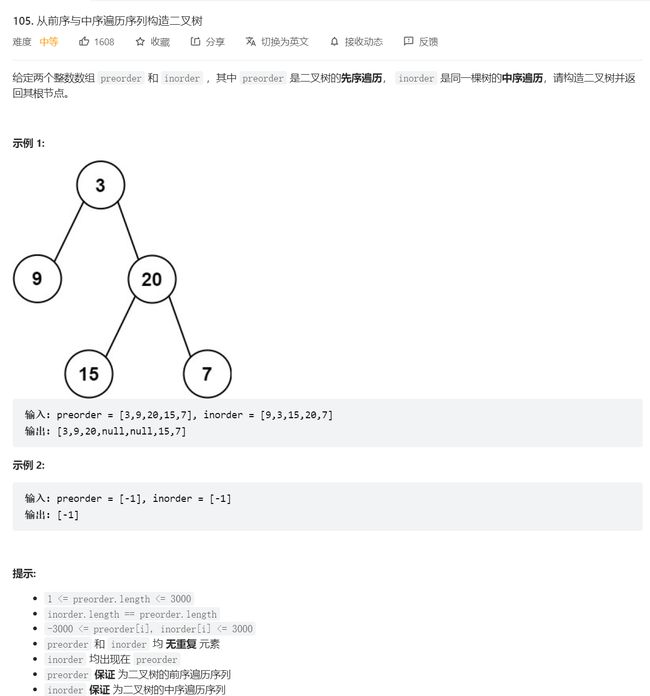
6.从前序与中序遍历序列构造二叉树
原题链接:从前序与中序遍历序列构造二叉树
算法思想:
- 对于前序遍历,我们得到的序列是
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ],对于中序遍历,我们得到的序列是[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]。 - 所以,我们可以通过前序序列找到根节点,然后在中序序列中找到根节点,这样就可以将划定出此根结点的左子树和右子树,然后递归创建左右子树,再将左右子树接到根结点上,返回根结点即可。
- 我们通过前序序列遍历这棵树,通过传递中序序列的开始下标和结束下标来(闭区间)划分一棵树,具体实现见代码:
代码实现:
class Solution {
public:
// 前序序列构建二叉树
TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend)
{
// 当中序的开始下标大于结束下标,说明这棵树不存在,返回nullptr
if(inbegin > inend)
return nullptr;
// 以当前前序结点创建树结点
TreeNode* root = new TreeNode(preorder[prei]);
// 在中序序列中找根节点
int rooti = inbegin;
while(rooti <= inend)
{
if(inorder[rooti] == preorder[prei])
break;
else
rooti++;
}
// 前序序列的下标++,遍历下一个根节点
prei++;
// 递归创建左右子树
// 左子树中序区间[inbegin, rooti - 1]
root->left = _buildTree(preorder, inorder, prei, inbegin, rooti - 1);
// 右子树中序区间[rooti + 1, inend]
// 注意在此时prei可能已经不是左子树传递的prei了,因为prei为引用,会实时改变
root->right = _buildTree(preorder, inorder, prei, rooti + 1, inend);
// 返回根结点
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
// 前序遍历从下标为0的根节点开始,注意prei传递的是引用类型,方便实时修改根节点下标
int prei = 0;
TreeNode* head = _buildTree(preorder, inorder, prei, 0, inorder.size() - 1);
return head;
}
};
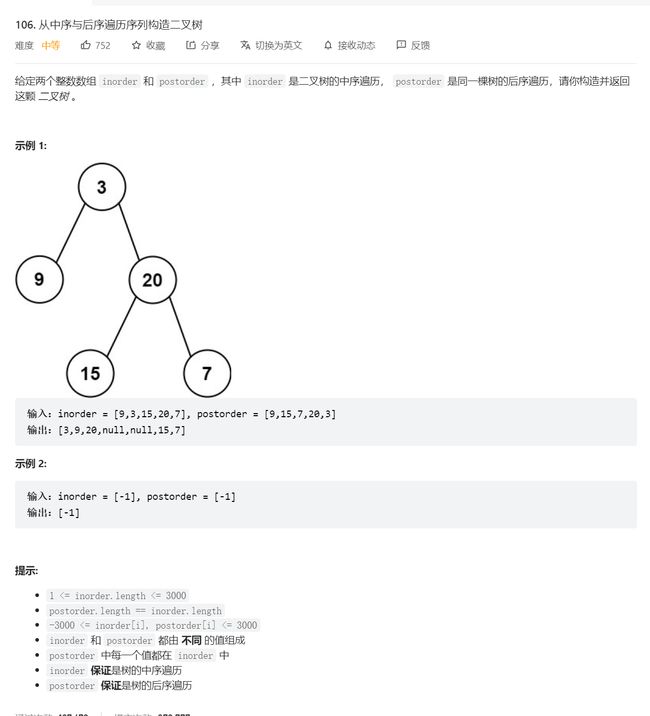
7.从中序与后序遍历序列构造二叉树
原题链接:从中序与后序遍历序列构造二叉树
算法思想:
- 对于后序,我们得到的序列是
[[左子树的前序遍历结果], [右子树的前序遍历结果],根节点],对于中序遍历,我们得到的序列是[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]。 - 所以,我们可以通过后序序列找到根节点(从后向前走),然后在中序序列中找到根节点,这样就可以将划定出此根结点的左子树和右子树,然后递归创建左右子树,再将左右子树接到根结点上,返回根结点即可。
- **特别注意:**如果从后向前遍历后序序列得到的顺序应该是
[根节点, [右子树的前序遍历结果],[左子树的前序遍历结果]],所以我们应该先创建右子树,再创建左子树,才能保证遍历的顺序和创建子树的顺序对应。 - 我们通过后序序列(从后向前)遍历这棵树,通过传递中序序列的开始下标和结束下标来(闭区间)划分一棵树,具体实现见代码:
代码实现:
class Solution {
public:
TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posti, int inbegin, int inend)
{
// 当中序的开始下标大于结束下标,说明这棵树不存在,返回nullptr
if(inbegin > inend)
return nullptr;
// 创建根节点
TreeNode* root = new TreeNode(postorder[posti]);
// 在中序序列中找根节点
int rooti = inbegin;
while(rooti <= inend)
{
if(inorder[rooti] == postorder[posti])
break;
else
rooti++;
}
// 后序序列从后向前,所以下标--
posti--;
// 先创建右子树,再创建左子树
root->right = _buildTree(inorder, postorder, posti, rooti + 1, inend);
root->left = _buildTree(inorder, postorder, posti, inbegin, rooti - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int posti = postorder.size() - 1;
TreeNode* head = _buildTree(inorder, postorder, posti, 0, inorder.size() - 1);
return head;
}
};
☂8.二叉树的前序遍历(非递归)
原题链接:二叉树的前序遍历
算法思想:
- 使用栈结构
st来模拟递归的情况,使用数组v存储遍历结果,cur表示当前遍历的结点cur初始值为root。 - 从
cur节点出发,如果cur的左子树不为空,将当前结点入栈,并且将当前结点cur对应的元素值加入v,再让cur向左走。直到cur的左子树为空。 - 将栈顶元素的
right赋给cur,并将栈顶结点出栈(与递归不同的是,递归是将右子树遍历完才出栈,这里将右子树给cur后就可以出栈了)。 - 重复上面两个过程,直到栈为空并且
cur为空。 - 简单来说:一棵树的访问分为:
- 遍历左路结点,将左路结点入栈。
- 依次出栈,遍历栈顶元素的右子树。
- 重复1,2过程,直到栈为空并且
cur为空。
代码实现:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
while (cur || !st.empty())
{
// 一直向左走
while (cur)
{
// 入栈cur
st.push(cur);
// 由于是前序序列,在入栈元素时就要将其元素值加入结果。
v.push_back(cur->val);
cur = cur->left;
}
// 访问栈顶元素的右子树
TreeNode* top = st.top();
st.pop();
cur = top->right;
}
return v;
}
};
☔9.二叉树的中序遍历(非递归)
原题链接:二叉树的中序遍历
算法思想:
- 中序与前序的思路基本相同唯一的区别就是:中序的顺序是
[左,根,右],所以直到将根结点出栈时(与递归不同的是,递归是将右子树遍历完才出栈,这里将右子树给cur后就可以出栈了),才能将根结点的元素值加入v。 - 使用栈结构
st来模拟递归的情况,使用数组v存储遍历结果,cur表示当前遍历的结点cur初始值为root。 - 从
cur节点出发,如果cur的左子树不为空,将当前结点入栈,再让cur向左走。直到cur的左子树为空。 - 将栈顶元素的
right赋给cur,将栈顶结点对应的元素值加入v,并将栈顶结点出栈。 - 重复上面两个过程,直到栈为空并且
cur为空。 - 简单来说:一棵树的访问分为:
- 遍历左路结点,将左路结点入栈。
- 依次出栈,遍历栈顶元素的右子树。
- 重复1,2过程,直到栈为空并且
cur为空。
代码实现:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
while (cur || !st.empty())
{
// 一直向左走
while (cur)
{
st.push(cur);
cur = cur->left;
}
// 出栈栈顶元素,并将其元素值加入v
TreeNode* top = st.top();
v.push_back(top->val);
st.pop();
// 开始遍历栈顶元素的右子树
cur = top->right;
}
return v;
}
};
⛱10.二叉树的后序遍历(非递归)
原题链接: 二叉树的后序遍历
算法思想:
- 后序遍历与上面两种遍历很不一样,因为后序遍历是
[左,右,根],所以后序遍历的根节点必须要等左右子树都遍历完才能加入v,在遍历到根节点是还必须要区分是否将左右子树全都遍历完。 - 有一种思路是用一个
pair结构记录有没有访问右子树,如果已经访问过,就可以出栈根节点,如果没有访问过,那就访问右子树,并且将bool值改为true。 - 但是上面方法的空间复杂度太高,我们采用另一种非常巧妙的方法,用一个变量
prev记录当前结点的前驱结点。根据后序遍历顺序,如果当前结点的前驱结点恰巧就是当前结点的右子树,那么说明当前结点的左右子树已经全部被访问完,根节点可以出栈。反之,如果当前结点的前驱结点不是当前结点的右子树,那么此时没有访问右子树,不能出栈。 - 使用栈结构
st来模拟递归的情况,使用数组v存储遍历结果,cur表示当前遍历的结点cur初始值为root。 - 从
cur节点出发,如果cur的左子树不为空,将当前结点入栈,再让cur向左走。直到cur的左子树为空。 - 如果满足栈顶结点的出栈条件,将根节点的元素值加入
v,更新prev。反之,将栈顶元素的right赋给cur,遍历右子树。 - 重复上面两个过程,直到栈为空并且
cur为空。
代码实现:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
TreeNode* cur = root, * prev = nullptr;
stack<TreeNode*> st;
vector<int> v;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
// 栈顶元素的右子树为空 或者 上一个出栈的元素是栈顶元素的右子树根 时
// 栈顶元素出栈(可能会有连续出栈,可自行画棵树验证)
if (top->right == nullptr || prev == top->right)
{
v.push_back(top->val);
st.pop();
prev = top;
}
else
{
cur = top->right;
}
}
return v;
}
};
后记
这次题目是二叉树这个面试最爱考的题目,比较考验大家的逻辑思维以及代码实现能力,相信大家做完会有所收获。
《二叉树经典进阶题目》——隶属于【刷题日记】系列,白晨开这个系列的目的是向大家分享经典的笔试编程题,以便于大家参考,查漏补缺以及提高代码能力。如果你喜欢这个系列的话,不如关注白晨,更快看到更新呀。
如果喜欢这个系列的话,不如订阅【刷题日记】系列专栏,更快看到更新哟
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦!
如果这篇文章有帮到你,还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧!喜欢白晨【刷题日记】系列的话,不如关注白晨,以便看到最新更新哟!!!