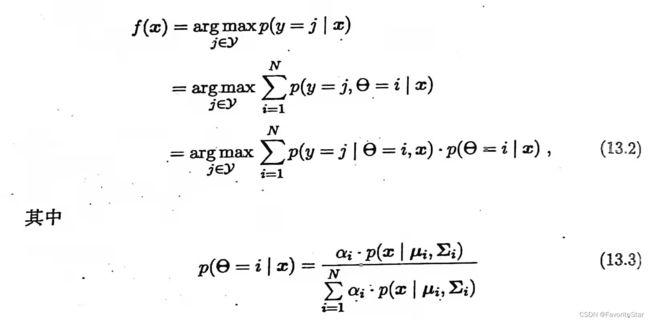【机器学习】之第十三章——半监督学习
13.1、未标记样本
在现实生活中,通常学习任务是已标记样本较少,而未标记的样本很多,那么按照传统监督学习的思想,便只能用已标记的少部分样本去训练学习器,这将会导致学习器的泛化性能不够好,因此如何利用起来这些未标记样本是重要需要思考的问题。
有一种常见的方法称为主动学习,可以用例子来简单理解:
- 对于有标记的数据集 D l D_l Dl,先用其训练一个模型,再用这个模型去未标记的数据集 D u D_u Du中挑选样本,再询问“专家”这个样本的标记信息,从而将新获得的有标记的样本加入 D l D_l Dl重新训练模型,然后再去挑选样本,以此类推
- 这样,若每次都能够挑选出对模型性能的改善帮助较大的样本,便可以利用较少的未标记样本,询问专家较少的次数,来训练出较强的模型,从而大幅度降低标记成本
显然,主动学习引入了额外的“专家知识”,通过与外界的交互来将部分未标注的样本转换为已标记样本。
另一种方式则为半监督学习,其不需要额外的“专家知识”,没有额外信息,仅利用未标记样本来提高泛化性能。
未标记样本虽然没有直接包含标注信息,但若它们与已标注样本是从同样的数据源独立同分布采样而来,则它们所包含的关于数据分布的信息对于建立模型很有帮助,利用下图,如果能够看到较多的未标注样本的分布,那么可以利用聚类当中的思想,较有把握地判断目标样本属于+类。
而要利用这些未标注样本,还需要进行一定的假设:
- 聚类假设:假设数据存在簇结构,同一个簇的样本属于同一个类别
- 流形假设:邻近的样本具有相似的输出值
这两个假设的本质都是相似的样本具有相似的输出。
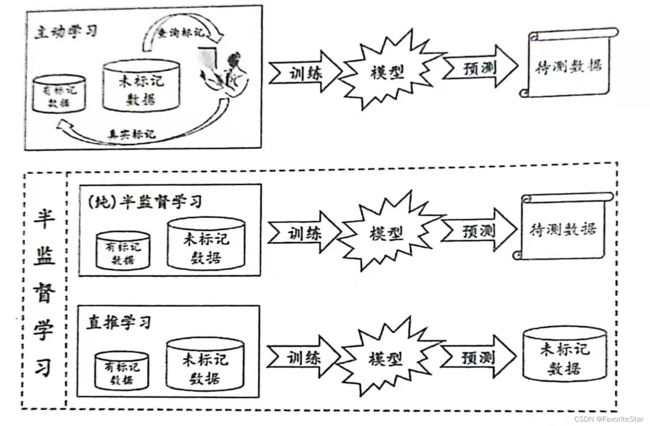
半监督学习可以进一步细分为纯半监督学习和直推学习,其重要的区别在于:
- 纯半监督学习:假定训练数据中的未标记样本并不是待预测的数据
- 直推学习:假设学习过程中所考虑的未标记样本就是待预测数据,学习的目的就是要在这些未标注样本上获得最优泛化性能
13.2、生成式方法
生成式方法的重要假设是所有数据(无论是否有标记)都是由同一个潜在的模型生成的,那么使得能通过潜在模型的参数将未标注数据与学习目标联系起来,而未标注数据的标注就可以看成是模型的缺失参数,通常可用EM算法来进行极大似然估计求解。
假设数据样本是由如下的高斯混合分布所产生的的:
p ( x ) = ∑ i = 1 N α i ⋅ p ( x ∣ μ i , Σ i ) p(x)=\sum_{i=1}^N \alpha_i ·p(x \mid \mu_i,\Sigma_i) p(x)=i=1∑Nαi⋅p(x∣μi,Σi)
且假设每个类别对应着一个高斯混合成分,即由真实类别标记为 Y = { 1 , 2 , 3 , . . . , N } Y=\{1,2,3,...,N\} Y={1,2,3,...,N}。令 f ( x ) f(x) f(x)为样本 x x x的标记,则由最大化后验概率可得:
其中, p ( y = j ∣ θ = i , x ) p(y=j \mid \theta=i,x) p(y=j∣θ=i,x)代表已知样本 x x x由第 i i i个高斯分布生成,其类别属于 j j j的概率,而前文已假设每个类别对应着一个高斯成分,那么有:
p ( y = j ∣ θ = i , x ) = p ( y = j ∣ θ = i ) = { 1 , j = i 0 , j ≠ i p(y=j \mid \theta=i,x)=p(y=j\mid \theta=i)\\=\begin{cases}1,\quad j=i\\0, \quad j\neq i\end{cases} p(y=j∣θ=i,x)=p(y=j∣θ=i)={1,j=i0,j=i
因为所属类别只与样本是属于哪一个高斯分布有关,与样本的具体无关。
那么可以发现:
- p ( y = j ∣ θ = i , x ) p(y=j \mid \theta=i,x) p(y=j∣θ=i,x)需要知道样本的标记,因此只能使用已标注数据
- p = ( θ i ∣ x ) p=(\theta_i \mid x) p=(θi∣x)不涉及样本标记,因此已标注和未标注数据都可以使用
因为可以通过引入大量的未标注数据,使得 p = ( θ i ∣ x ) p=(\theta_i \mid x) p=(θi∣x)这一项的估计能够由于数据量的增大而变得更加准确,从而使得上面关于 f ( x ) f(x) f(x)的计算式子也更加准确,从而提高分类器的性能。
因此,若给定已标注样本集 D l D_l Dl和未标注样本集 D u D_u Du, l ≪ u , l + u = m l \ll u,l+u=m l≪u,l+u=m,同时假设所有样本独立同分布,且都是由同一个高斯混合模型生成的,则可以用极大似然法估计高斯混合模型的参数,即:
此部分的推导可以查看我关于第九章聚类的博客,里面关于GMM模型的推导较为详细,理解起来较为容易
上述过程是假设生成模型为高斯混合模型,也可以替换成其他的模型,也是相同的思路。但此类方法的关键在于假设的生成模型必须准确,即必须与真实数据的分布吻合,否则利用未标注数据反而会使得泛化性能下降。
13.3、半监督学习SVM
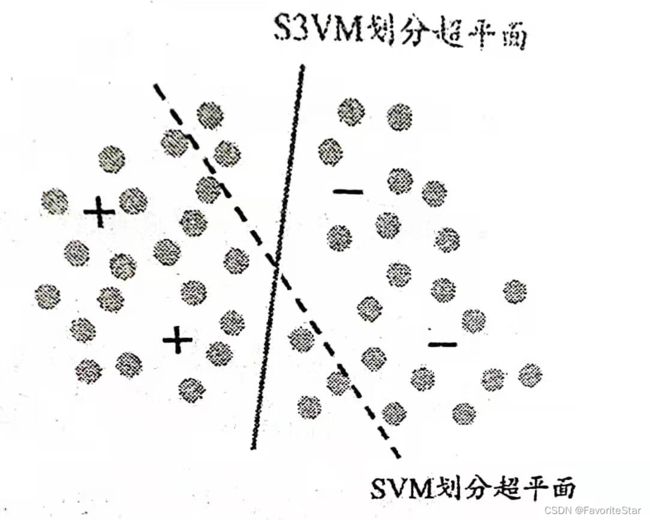
S3VM的思想就是在考虑未标注样本后,试图找到能够将两类有标注样本分开,同时穿过数据低密度区域的划分超平面,如下图:
在半监督支持向量机中最著名的算法为TSVM,是一个针对二分类的算法,其思想关键是尝试将每个未标记样本分别作为正类和负类,然后在所有这些结果中,寻求一个在所有样本(包括标注与未标注)上间隔最大化的划分超平面。一旦划分超平面确定,则未标注样本的最终标记就是其预测结果。
但遍历所有可能的结果计算量太大了,因此TSVM是采用局部搜索的方式来迭代寻找近似解的,即:
文字描述为:
- 先利用已标注的样本学习得到一个SVM,利用这个SVM对未标注的样本进行标记指派(即为它们添加标注),那么此时 y ^ \hat{y} y^即已知,那么就可以代入上图中的(13-9)来求解出新的划分超平面和各个松弛变量(此时未标注样本的标记指派可能是不正确的,因此 C u C_u Cu要设置得比 C l C_l Cl小,让已标注样本发挥较大的作用)
- 找出两个进行了标志指派的样本,它们满足指派的类别不相同(一个为正一个为负),并且松弛变量较大(即可能发生了分类错误),交换它们的标记,然后再基于(13-9)求解新的划分超平面和松弛变量
- 再找出两个满足上一个条件的进行了标记指派的样本,再次交换标记并且重新求解,直到没有满足条件的样本
- 增大 C u C_u Cu,再进行上面三步的循环,直到 C u = C l C_u=C_l Cu=Cl为止
13.5、基于分歧的方法
该方法与之间所述的各种方法对于未标注数据的利用方式不同,基于分歧的方法是使用多学习器,而学习器之间的“分歧”对于未标注数据的利用尤为重要。此类方法最主要的代表为协同训练,其最初是针对“多视图数据”而设计的。因此首先介绍何为多视图数据。
在现实中,一个数据对象往往拥有多个属性集,每个属性集就构成了一个视图,例如对于一部电影来说,可以简单的采用图像画面属性集所构成的视图和声音属性集所构成的视频,那么一个电影片段就可以表示为样本 ( < x 1 , x 2 > , y ) (
不同视图之间具有以下特性:
- 相容性:即其所包含的关于输出空间 y y y的信息是一致的,例如 Y 1 Y^1 Y1是 x 1 x^1 x1判别出来的标记空间(可能不止一个标记), Y 2 Y^2 Y2是 x 2 x^2 x2判别出来的标记空间,那必然有 Y 1 = Y 2 Y^1=Y^2 Y1=Y2。
- 互补性:例如从图像视图看见两个人对视,如果能够加上声音视图听见情话那么就说明是爱情片
而协同训练正是利用了多视图数据的相容互补性,但对数据有两个前提假设:
- 充分:是指每个视图都包含足以产生最优学习器的信息
- 条件独立:是指在给定类别标记条件下两个视图独立
那么在此假设下,协同训练对于未标记的数据利用方式为:首先在每个视图上基于有标记的样本分别训练处一个分类器,然后让每个分类器分别取挑选自己最有把握的未标记样本赋予伪标记(即置信度最高的),并将伪标记样本提供给另一个分类器作为新增的有标记样本进行训练更新,这个过程不断迭代,直到两个分类器都不发生变化或者达到迭代次数为止。算法描述如下:
13.6、半监督聚类
聚类是典型的无监督学习任务,然后在现实中,我们可能会获得一些额外的信息来帮助我们进行聚类,因此对这些信息进行利用,就可以称为半监督聚类。
聚类任务中能够获得的监督信息大致可以分为两类:
- 必连与勿连:前者指两个样本必须属于同一个簇,后者指两个样本必须不属于同一个簇
- 少量的有标记样本
约束k均值算法就是利用必连与勿连信息的算法,它需要给定样本集和必连关系集合 M M M以及勿连关系集合 C C C,其算法流程与k均值算法类似,只是加入了必连与勿连关系的考虑。其算法描述如下:
而约束种子k均值算法则是对第二类信息的利用,即已知有少量的有标记样本:给定样本集 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={x1,x2,...,xm}以及少量有标记的样本 S = ⋃ j = 1 k S j ⊂ D S=\bigcup_{j=1}^k S_j \subset D S=⋃j=1kSj⊂D,其中 S j S_j Sj为隶属于第j个聚类簇的样本。此信息的利用方式为:直接将它们作为种子,用来初始化k均值算法的k个聚类中心,重点是在迭代过程中不改变种子样本所属于的类别。其算法描述如下: