数学建模——多元线性回归 /多元线性拟合 (工具：matlab)

---

技巧篇

数学建模系列文章——总结篇：《数模美一国一退役选手的经验分享[2021纪念版]》.

---

一、多元线性回归是什么

  我用一个公式来描述：$$f(x_1,x_2,...,x_n)={\alpha }_1\times x_1+{\alpha }_2\times x_2+...+{\alpha }_n\times x_n+\beta$$  ①其中，$x_1,x_2,...,x_n$ 分别表示 1号自变量、2号自变量、…、n号自变量。

  ②$f(x_1,x_2,...,x_n)$ 表示受这些自变量共同影响而 线性合成 的因变量。

  ③${\alpha }_1、{\alpha }_2、...、{\alpha }_n$ 分别表示待拟合的系数。

  ④$\beta$ 表示待拟合的常数。

---

二、样例及代码

	话不多说，直接上例子，

  “综合打分” 是 去年 体育老师根据这15名同学的体重、肺活量、50m短跑、1分钟仰卧起坐、跳远成绩、1000米成绩、1分钟跳绳、引体向上、坐位体前屈等等数据综合评价打出的分数。

  今年 因为学校器材有限，体育老师只测了这15名同学的三项指标：跳远成绩、1000米成绩、1分钟跳绳。

  现在体育老师想要知道这三项指标能不能 线性合成 成最后的 今年 的综合分数?

  

第一步：画散点图进行分析

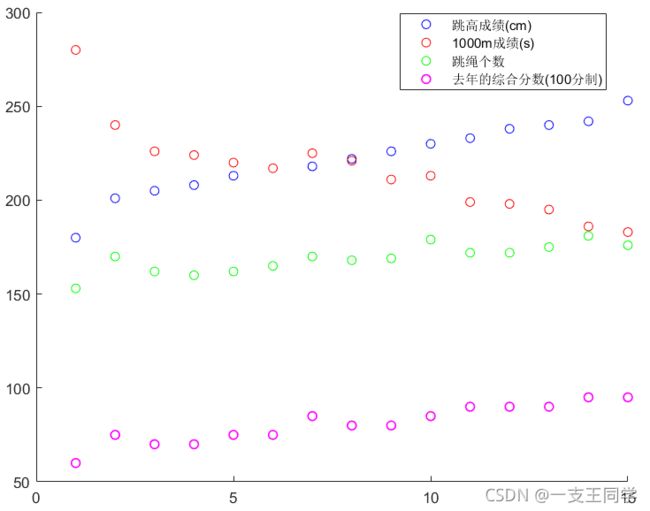
clc;clear;close all;
x1 = [180	201	205	208	213	217	218	222	226	230	233	238	240	242	253]';  % 跳高成绩
x2 = [280 240 226 224 220 217 225 221 211 213 199 198 195 186 183]';    % 1000m成绩
x3 = [153 170 162 160 162 165 170 168 169 179 172 172 175 181 176]';    % 跳绳个数
Y = [60	75 70 70 75	75 85 80 80	85 90 90 90	95 95]';                    % 综合打分

figure(1);
hold on;
plot(x1,'bo');
plot(x2,'ro');
plot(x3,'go');
plot(Y,'mo','LineWidth',1);
legend('跳高成绩(cm)','1000m成绩(s)','跳绳个数','去年的综合分数(100分制)')

运行结果如下：

  从上图中可以直观地看出，去年的综合分数 大致是线性递增。同样的，跳远成绩、1000米成绩、1分钟跳绳三项指标也是线性地变化，所以我们有理由推断，这三项指标能 线性合成 成最后的综合分数。

第二步：拟合

  在百度、CSDN、博客上找了很久都没有找到很好的源码。无奈，自己动手干吧

  原理可以参考这篇文章《数学建模——基于 最小二乘法 的 回归分析》https://blog.csdn.net/Wang_Dou_Dou_/article/details/118971407?spm=1001.2014.3001.5501

  综合看了很多资料后，终于敲好了。 ‍♂

% 因为用的3是维拟合，则 x 应该为 3*15 的矩阵，第一列为 1 ，第二列为 x1 ，第三列为 x2 , 第四列为 x3
% 15 代表的是 样本个数
len = length(Y);
pelta = ones(len,1);
x = [pelta, x1, x2, x3];

[b,bint,r,rint,stats]=regress(Y,x,0.05);     % 95%的置信区间

Y_NiHe = b(1) + b(2) .* x1 + b(3) .* x2 + b(4) .* x3 ;

figure(2);
hold on;
plot(x1,'bo-');
plot(x2,'ro-');
plot(x3,'go-');
plot(Y,'mo-');
plot(Y_NiHe,'kx-','LineWidth',1);
legend('跳高成绩(cm)','1000m成绩(s)','跳绳个数','去年的综合分数(100分制)','多元线性回归拟合曲线')
R_2 = 1 - sum( (Y_NiHe - Y).^2 )./ sum( (Y - mean(Y)).^2 );
str = num2str(R_2);
disp(['拟合优度为：',str])
                  

运行结果如下：

$$拟合优度R^2=0.94903$$

  在上图中，黑色的就是多元线性回归拟合曲线。 可以看出，拟合结果和去年的综合分数想贴近，误差不大。

说明：
  ①regress()中的 $\alpha$ 为显著性水平(缺省时默认为0.05)

  ②b，bint 为 回归系数估计值 和 它们的置信区间

  ③r，rint 为 残差(向量) 及其 置信区间

  ④stats 是用于检验回归模型的统计量，有4个数值，第一个是拟合优度 R²，第二个是 对方程整体显著性检验 的 F检验 ，第三个是 p值，第四个是 误差方差的估计值 $s^2$ 。

参数运行结果：

  由上图可知，R²=0.9490 表示因变量 $y$(综合分数) 的94.90%可由模型确定，F值 远远超过 F检验的临界值，p 远小于 $\alpha$，因而该回归模型从整体来看是可用的。

补充： F检验 、 p值 、误差方差s² 的原理详见文章最后的 参考附录[2]、[3]、[4]

  上图中 列向量$b$ 中存放的是拟合的系数和常数项。$b(1)$ 为常数项，$b(2)、b(3)、b(4)$ 分别为 $x_1、x_2、x_3$ 的系数。

  得到最终表达式如下：
$$y=f(x_1,x_2,x_3)=-107.6271+0.4190\times x_1+0.0576\times x_2+0.4931\times x_3$$

---

三、总结：

  第一步：画散点图进行分析

  第二步：ctrl+c/v

  最后，我没有详细地阐述其原理，只阐述了有什么用、怎么用。如要了解详细的原理，可以看看文章最后的 参考附录 吧。

---

四、参考附录：

[1] 《数学建模——区分“拟合、插值、多元线性回归、逻辑回归、逐步回归、最小二乘法”等概念【概念篇】》
链接: https://blog.csdn.net/Wang_Dou_Dou_/article/details/118739458?spm=1001.2014.3001.5501.

[2] 《F检验》
链接: https://baike.baidu.com/item/F%E6%A3%80%E9%AA%8C/9910842?fr=aladdin.

[3] 《P值》
链接: https://baike.baidu.com/item/P%E5%80%BC.

[4] 《如何用stata求误差方差 s² 的估计值》 看追问的那条回复即可
链接: https://zhidao.baidu.com/question/397143810094044805.html.

[5] 《最小二乘法多元线性回归_使用Matlab解决多元线性回归问题》这里面有教如何清理异常数据
链接: https://blog.csdn.net/weixin_39636645/article/details/112712714.

数学建模系列文章——总结篇：《数模美一国一退役选手的经验分享[2021纪念版]》.

---

搜集资料码字码图，封装代码不易，多多支持~ ☁️ ☁️