（pytorch进阶之路）NormalizingFlow标准流

导读

概述

NF和GAN一样是一个生成模型，NF与GAN不同的是，GAN是以模糊的方式对目标数据分布进行建模， 没有直接写出px的表达式，而是将x送入下游的判别器做分类任务，通过对抗的方式让生成器生成比较好的效果

而标准流NF可以显式地将目标的表达式px写出来，通过优化对数似然函数达到最大去调整参数，使得模型很好的拟合目标分布

标准流模型是一个可逆的模型，也就是训练的时候，是从x到z的变化过程，最大化似然函数，推理时候就反过来使用，以一个随机变量z作为输入，把网络完全逆过来，计算反函数，算出x

设计巧妙的变换，使得似然函数容易计算，并且逆变换也很容易计算。

在给定数据分布的情况下，似然函数是什么，给定可定的数据，我们认为这个模型输出结果反应数据存在可能性有多大

NF训练和推理阶段是可并行的，而像自回归推理在解码阶段就不能并行而是递归的

NF使用的是可能的1×1的卷积，1×1的卷积抛弃了传统卷积的局部建模思路，而看作是一个作用在通道层的MLP网络，1×1的卷积做的是通道融合机制，在transformer中也有这一类似的思路，mhsa和FFN，mhsa做的事emb与周围的emb时间关联性，FFN做的事就是通道融合

给定一个数据集D，可以写出它的对数似然函数

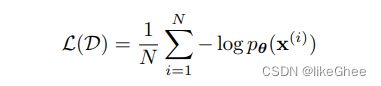
大部分基于flow的生成式模型，定义有：
从pθ分布中采样随机变量z
z送入gθ变换函数中得到x，x就是训练集，也是最终要预测的目标数据

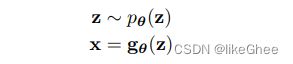
pθ有一个可解的概率密度函数（PDF），比如高斯分布

gθ是可逆的（也可以说是双射的），那么就能从gθ的反函数得到z

什么是标准流呢，z = fθ(x) = gθ-1(x)

fθ是由一系列变换函数嵌套构成，f=f1·f2·…fk

那么x和z之间的关系就可以写成下面形式：

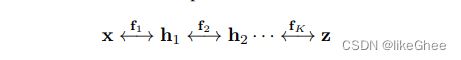
上述过程就成为Normalizing Flow：将可见数据分布x变为标准分布z

可见数据x的似然函数（概率密度函数）为：

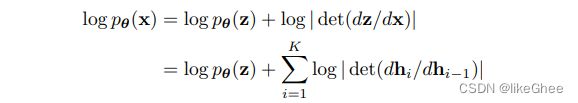
x的pdf可以写成z的pdf 乘以 z关于x的雅可比矩阵的行列式的绝对值：pdf(x) = pdf(z) × |det(dz/dx)|
两边取log就是上图公式，理解就是从hi-1到hi变化，每变换一步就增加对数的概率密度改变量一点

进一步理解x -> z -> x，从x到z，z到x，经过两次变换还原，两步分别得到log-det1和log-det2，jacob1和jacob2，x到z增加的对数概率密度是log-det1，z到x增加的对数概率密度是log-det2，那么log-det1+log - det2应该抵消了等于0，那么log-det1和log-det2就是相反数的关系

关于dz/dx推导部分，根据求导的链式法则，x <-> h1 <-> h2 … <->z，其中记h0=x, hk=z
=> 则dz/dx可以写成 Π[i=从1到k] dhi/dhi-1，取对数就是上图公式所示

pdf(z)是标准分布的概率密度函数，加法后面的一项可以写出来，那么pdf(x)就能写出来 ，两边取对数，对log批次取一个负号，就能用梯度下降算法优化参数，最小化负对数似然即可

置换矩阵行列式det为0，三角矩阵det为斜对角线的乘积，这类矩阵的det比较好计算

我们保证jacobian矩阵dhi/dhi-1矩阵是一个三角矩阵的话就十分好计算了，取个log就是对角线元素相加了：

flow结构详解

生成式flow由一系列单步的flow构成，这个单步flow，是可逆的，输入可以输出，输出可以输入，每步的log-det也能写出来

每个flow包含三个串行部分：
第一部分：激活的归一操作
第二部分：可逆的1×1卷积
第三部分：耦合层

深度是k，由k个flow串联

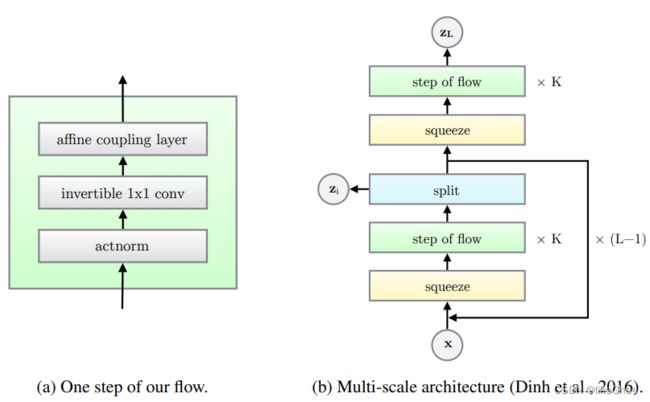
下表是三个主要部分，函数和逆函数以及log-det

x表示每层输入，y表示每层的输出，x和y都是[h×w×c]的三维张量，i和j表示h和w的索引，NN表示非线性变换，决定了整个网络的表达能力

Multi-Scale结构

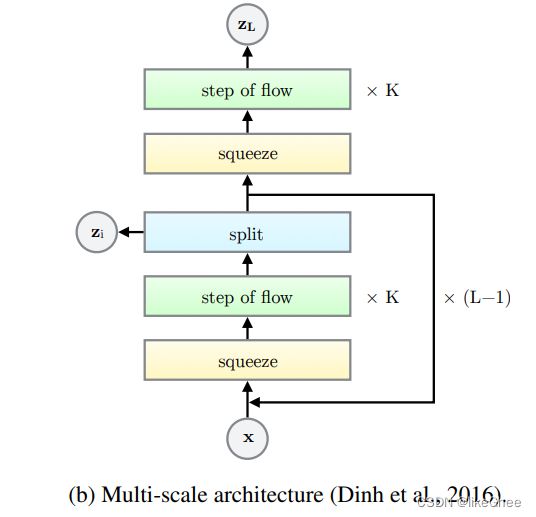
multi-scale结构（Multi-Scale结构实现了模型对不同尺度物体和特征的关注）
论文：https://arxiv.org/pdf/2007.09384.pdf

每个block会划分一个zi，每个block先预测出一半的z，另一半作为下一个block的输入，下个block再分出一半的z，逐渐的去预测z，而不是一次性预测z，这样通道数越来越少，减少计算量

multi-scale结构中间层就是step of flow 单步flow，下面是flow结构每部分详解

Actnorm

第一部分是Actnorm，激活归一化层，per channel ( c )的仿射变换，对每个通道进行操作
对于任意的i和j，

前向运算：yij=s element_× xij + b，yij、xij和b都是长度为channel大小的向量，s是缩放权重，b是偏置量
逆函数：x=(y-b)/s

关于log-det(dy/dx)：
x到y的雅可比矩阵，因为是element-wise乘法，所以雅可比矩阵就是对角矩阵
举例
现有公式①
①：[x1, x2, x3] ele-× [w1, w2, w3] = [y1, y2, y3]
记 s = [w1, w2, w3]

那么①的雅可比矩阵：
[[dy1/dx1 = w1 , dy1/dx2 = 0, dy1/dx3 = 0]
[dy2/dx1 = 0, dy2/dx2 = w2, dy2/dx3 = 0]
[dy3/dx1 = 0, dy3/dx2 = 0, dy3/dx3 = w3]]

那么一个点的log-det = sum(log |s|)，所有点log-det在×一个h和w log-det = h · w · sum(log|s|)

s和b的初始化目的是使得进入后面的网络的输入在每个通道上是mean=0，std=1，因此s和b初始化依赖于第一批数据的，计算每个通道数的均值和方差，s=1/方差，b=-mean，可以看作是数据依赖的初始化

这样的做法有些奇怪，其实我们预处理的时候就将数据归一化再输入了

可逆的1×1卷积

kernel_size = W = [c×c×1×]

前向运算：yij = W @ xij， [c, c] @ [c, 1] => [c, 1]

逆运算：xij = W-1 @ yij，[c, c] @ [c, 1] => [c, 1]

对数似然增量log-det(dy/dx)：
yij = W@xij ，其实这个式子的雅可比矩阵就是W，那计算W的det行列式，直接硬求log(det(W))，复杂度是n3次方，
log-det = h · w · log(|det(W)|)
直接计算det(W)复杂度计算复杂，另一种方法是LU分解，

W = PL(U + diag(s))，
P是一个排列矩阵（单位矩阵经过行列交换而得到的新矩阵，每行或每列上有且仅有一个1，其他元素都为0），
L是下三角矩阵但是对角线元素是1，
U是上三角矩阵但是对角线元素是0，
diag(s)是以s为对角线的矩阵，
矩阵相乘的行列式也相乘，那么log-det(W) = sum|log(s)|
类似权重归一化，后续只更新PLU矩阵

仿射耦合层

前向运算：
第一步，x拆分成xa和xb，这个拆分是在通道维度上做的[c, ] -> [ca, ] 和 [cb,]，ca和cb满足ca+cb=c
第二步，将xb送入神经网络NN得到s和t
第三步，xa，s和t经过仿射变换得到ya，ya= xa×s + t
第四步，yb直接等于xb

逆运算：
yb直接就等于xb，这步很简单
关键是ya如何变为xa，得到xb后计算的得出s和t，(ya - t) / s = xa

对数似然增量log-det：
计算雅可比矩阵
ya= xa×s + t =>
dya/dxa = diag(s)
dya/dxb是一个比较复杂的矩阵

yb = xb =>
dyb/dxa = 0
dyb/dxb = 全1矩阵

合起来整体雅可比矩阵为
[[diag(s), 复杂矩阵],
[全0矩阵, 全1矩阵]]
整体雅可比矩阵就是一个上三角矩阵，因此det行列式就是det(diag(s)) = sum(s)，与NN是什么形式无关

=> 概率密度增量为sum(log|s|)

论文地址

https://proceedings.neurips.cc/paper/2018/file/d139db6a236200b21cc7f752979132d0-Paper.pdf

代码地址

https://github.com/rosinality/glow-pytorch

实现

model.py和train.py，实现很简洁

model有三层act norm，1×1convolution，affine coupling layer，将每个模块都写成了class，最终汇总成一个flow step，很多个flow step则构成了一个glow。则一共有五个模块

actnorm

归一化层，其实这一层就是对batch做归一化，减去mean再除以std

class ActNorm(nn.Module):
    def __init__(self, in_channel, logdet=True):
        # logdet 函数的对数值，计算对数行列式的值
        # s ele_× x + b，s和b的in_channel有关
        super().__init__()
        # 平移量，nn.Parameter 可训练参数，写成input的形状
        self.loc = nn.Parameter(torch.zeros(1, in_channel, 1, 1))
        # 伸缩量
        self.scale = nn.Parameter(torch.ones(1, in_channel, 1, 1))

        self.register_buffer("initialized", torch.tensor(0, dtype=torch.uint8))
        # buffer量 相当于下面的实例化，作用是一个标志位
        # self.initialized = nn.Parameter(torch.tensor(0, dtype=torch.uint8), requires_grad=False)
        # s和b是和batch有关的统计量，在第一次运行的时候需要去计算，初始化之后置为1
        self.logdet = logdet

    def initialize(self, input):
        with torch.no_grad():
            flatten = input.permute(1, 0, 2, 3).contiguous().view(input.shape[1], -1)
            mean = (
                flatten.mean(1)
                .unsqueeze(1)
                .unsqueeze(2)
                .unsqueeze(3)
                .permute(1, 0, 2, 3)
            )
            # mean = torch.mean(input, dim=[0,2,3], keepdim=True)
            # std = torch.std(input, dim=[0,2,3], keepdim=True)
            std = (
                flatten.std(1)
                .unsqueeze(1)
                .unsqueeze(2)
                .unsqueeze(3)
                .permute(1, 0, 2, 3)
            )

            self.loc.data.copy_(-mean)
            self.scale.data.copy_(1 / (std + 1e-6))

    def forward(self, input):
        bs, _, height, width = input.shape

        # 如果没有做initialize，则初始化
        if self.initialized.item() == 0:
            self.initialize(input)
            # 标注成1，表示已经初始化了
            self.initialized.fill_(1)

        log_abs = logabs(self.scale)
        # log-det计算，对数似然的增量
        logdet = height * width * torch.sum(log_abs)

        if self.logdet:
            return self.scale * (input + self.loc), logdet

        else:
            return self.scale * (input + self.loc)

    def reverse(self, output):
        # 推理的时候走reverse
        return output / self.scale - self.loc

可逆1×1卷积层

本质上1×1就是一个MLP，比较简单
细节是用了PLU分解
LU分解前提是矩阵不为0，正交矩阵行列式不为0，对任意矩阵做qr分解得到正交矩阵
只对通道进行融合
逆过程推理过了，reverse函数实现

class InvConv2dLU(nn.Module):
    # LU快速分解
    def __init__(self, in_channel):
        super().__init__()

        weight = np.random.randn(in_channel, in_channel)
        # qr正交分解
        q, _ = la.qr(weight)
        # lu分解，plu
        w_p, w_l, w_u = la.lu(q.astype(np.float32))
        # 取对角线元素作为向量
        w_s = np.diag(w_u)
        # 对w_u取上三角部分，从第一条对角线开始取，对于一个方阵而言中间的是第0条
        w_u = np.triu(w_u, 1)
        # mask，左下角和中间一条对角线元素都为0，右上角为1
        u_mask = np.triu(np.ones_like(w_u), 1)
        # 转置，下三角元素除对角线全1
        l_mask = u_mask.T

        w_p = torch.from_numpy(w_p)
        w_l = torch.from_numpy(w_l)
        w_s = torch.from_numpy(w_s)
        w_u = torch.from_numpy(w_u)

        # w_p是固定的，不需要更新
        self.register_buffer("w_p", w_p)
        # 使用register_buffer设置成无需更新的量
        self.register_buffer("u_mask", torch.from_numpy(u_mask))
        self.register_buffer("l_mask", torch.from_numpy(l_mask))
        # 对角线向量符号
        self.register_buffer("s_sign", torch.sign(w_s))
        # 对角线全为1的对角矩阵
        self.register_buffer("l_eye", torch.eye(l_mask.shape[0]))
        # 三个要更新的量
        self.w_l = nn.Parameter(w_l)
        self.w_s = nn.Parameter(logabs(w_s))
        self.w_u = nn.Parameter(w_u)

    def forward(self, input):
        _, _, height, width = input.shape
        # 重新拼凑回weight
        weight = self.calc_weight()

        out = F.conv2d(input, weight)
        logdet = height * width * torch.sum(self.w_s)

        return out, logdet

    def calc_weight(self):
        weight = (
            self.w_p
            # 因为w_l是在训练而变化的，l_mask下三角元素除对角线全1
            @ (self.w_l * self.l_mask + self.l_eye)
            @ ((self.w_u * self.u_mask) + torch.diag(self.s_sign * torch.exp(self.w_s)))
        )

        return weight.unsqueeze(2).unsqueeze(3)

    def reverse(self, output):
        weight = self.calc_weight()

        return F.conv2d(output, weight.squeeze().inverse().unsqueeze(2).unsqueeze(3))

仿射耦合层

分割x，传入NN（神经网络），NN不影响求解复杂度，只影响表示分布的质量，filter_size确定NN中的卷积的卷积核数目大小，

代码中NN最后一层使用ZeroConv2d，全0卷积（weight和bias全0），目的是为实现残差的效果，恒等变换的效果。

如果使用affine输出两部分log s和t，不做affine输出一半的channel就好

forward的时候使用chunk分割数据x

affine走的仿射的话，将x送入NN，将NN输出结果再分为两部分，logs和t
将logs取sigmoid得到s
用分割的x_b缩放平移得到out_b
x_a和out_b拼接输出为结果

不走affine，则xa和xb之间没有coupling（耦合），只是简单的加法

class ZeroConv2d(nn.Module):
    def __init__(self, in_channel, out_channel, padding=1):
        super().__init__()

        self.conv = nn.Conv2d(in_channel, out_channel, 3, padding=0)
        self.conv.weight.data.zero_()
        self.conv.bias.data.zero_()
        self.scale = nn.Parameter(torch.zeros(1, out_channel, 1, 1))

    def forward(self, input):
        out = F.pad(input, [1, 1, 1, 1], value=1)
        out = self.conv(out)
        out = out * torch.exp(self.scale * 3)

        return out


class AffineCoupling(nn.Module):
    def __init__(self, in_channel, filter_size=512, affine=True):
        super().__init__()

        self.affine = affine

        self.net = nn.Sequential(
            nn.Conv2d(in_channel // 2, filter_size, 3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(filter_size, filter_size, 1),
            nn.ReLU(inplace=True),
            ZeroConv2d(filter_size, in_channel if self.affine else in_channel // 2),
        )

        self.net[0].weight.data.normal_(0, 0.05)
        self.net[0].bias.data.zero_()

        self.net[2].weight.data.normal_(0, 0.05)
        self.net[2].bias.data.zero_()

    def forward(self, input):
        in_a, in_b = input.chunk(2, 1)

        if self.affine:
            log_s, t = self.net(in_a).chunk(2, 1)
            # s = torch.exp(log_s)
            s = F.sigmoid(log_s + 2)
            # out_a = s * in_a + t
            out_b = (in_b + t) * s

            logdet = torch.sum(torch.log(s).view(input.shape[0], -1), 1)

        else:
            net_out = self.net(in_a)
            out_b = in_b + net_out
            logdet = None

        return torch.cat([in_a, out_b], 1), logdet

    def reverse(self, output):
        out_a, out_b = output.chunk(2, 1)

        if self.affine:
            log_s, t = self.net(out_a).chunk(2, 1)
            # s = torch.exp(log_s)
            s = F.sigmoid(log_s + 2)
            # in_a = (out_a - t) / s
            in_b = out_b / s - t

        else:
            net_out = self.net(out_a)
            in_b = out_b - net_out

        return torch.cat([out_a, in_b], 1)

FlowStep

三个部分拼接成一个flow
实例化三个层，actnorn，1×1conv，affinecoupling
forward中依次经过三层
reverse则依次反过来调用三个层的reverse函数即可

class Flow(nn.Module):
    def __init__(self, in_channel, affine=True, conv_lu=True):
        super().__init__()

        self.actnorm = ActNorm(in_channel)

        if conv_lu:
            self.invconv = InvConv2dLU(in_channel)

        else:
            self.invconv = InvConv2d(in_channel)

        self.coupling = AffineCoupling(in_channel, affine=affine)

    def forward(self, input):
        out, logdet = self.actnorm(input)
        out, det1 = self.invconv(out)
        out, det2 = self.coupling(out)

        logdet = logdet + det1
        if det2 is not None:
            logdet = logdet + det2

        return out, logdet

    def reverse(self, output):
        input = self.coupling.reverse(output)
        input = self.invconv.reverse(input)
        input = self.actnorm.reverse(input)

        return input

Block

K个flow为一组，一组flow前加squeeze，后加split构成一个block，block重复L-1次

实现L-1次block结构

对in_channel×4得到squeeze dim，将通道数扩成4倍，

循环n_flow次，组合成k个flow

split源自NVP论文，multi-scale结构，每一层直接输出一半的z，和一半的output作为下一层的输入，随着层数的增加，计算的复杂度是越来越小。

如果有split，则输入in_channel×2，输出in_channel×4
如果没有split，输入in_channel×4，输出in_channel×8

如果是生成图片任务，可以加入condition，使用embedding表达，再将embedding映射到in_channel×4上（和h_zero形状一致）

---

在forward中
对input的通道和空间进行一定的缩放，通道扩大成4倍，空间的长和宽缩小自原来的一半，squeeze操作，空间部分挤压到通道上

遍历每个flow，nn.ModuleList，只有继承自Module里的参数才能成为整个模型的参数，用List的时候梯度更新会被忽略

要split，最后一个的flow的输出分割成两部分，一个是out，另一半是z作为输出

为了计算所有z的联合概率，求log pz，使用可学习的先验分布prior（不是标准分布），out作为输入得到mean和log_sd，则mean和log_sd是可学习的，我们定义了一个可学习的张量h_zero初始值为0，h_zero+condition送入到prior卷积层，分割为mean和log_sd

split：z_new，mean，log_sd送入高斯log p 得到log p，得到z的对数似然

不走split的话，直接将out送入到高斯log p

高斯log p：高斯密度函数再取一个log

---

reverse就反过来，

split的话就从z和x推出新的x，
z和x拼接送入prior，得到mean和log_sd，根据mean和log_sd从eps正态分布中采样，再乘以log_sd加上mean进行参数重整化，得到z，z和output拼接起来得到inout

没有split，直接将z作为input

对flow进行reverse

再对通道数缩小，长和宽扩大

class Block(nn.Module):
    def __init__(self, in_channel, n_flow, split=True, affine=True, conv_lu=True):
        super().__init__()

        squeeze_dim = in_channel * 4

        self.flows = nn.ModuleList()
        for i in range(n_flow):
            self.flows.append(Flow(squeeze_dim, affine=affine, conv_lu=conv_lu))

        self.split = split

        if split:
            self.prior = ZeroConv2d(in_channel * 2, in_channel * 4)

        else:
            self.prior = ZeroConv2d(in_channel * 4, in_channel * 8)

    def forward(self, input):
        b_size, n_channel, height, width = input.shape
        squeezed = input.view(b_size, n_channel, height // 2, 2, width // 2, 2)
        squeezed = squeezed.permute(0, 1, 3, 5, 2, 4)
        out = squeezed.contiguous().view(b_size, n_channel * 4, height // 2, width // 2)

        logdet = 0

        for flow in self.flows:
            out, det = flow(out)
            logdet = logdet + det

        if self.split:
            out, z_new = out.chunk(2, 1)
            mean, log_sd = self.prior(out).chunk(2, 1)
            log_p = gaussian_log_p(z_new, mean, log_sd)
            log_p = log_p.view(b_size, -1).sum(1)

        else:
            zero = torch.zeros_like(out)
            mean, log_sd = self.prior(zero).chunk(2, 1)
            log_p = gaussian_log_p(out, mean, log_sd)
            log_p = log_p.view(b_size, -1).sum(1)
            z_new = out

        return out, logdet, log_p, z_new

    def reverse(self, output, eps=None, reconstruct=False):
        input = output

        if reconstruct:
            if self.split:
                input = torch.cat([output, eps], 1)

            else:
                input = eps

        else:
            if self.split:
                mean, log_sd = self.prior(input).chunk(2, 1)
                z = gaussian_sample(eps, mean, log_sd)
                input = torch.cat([output, z], 1)

            else:
                zero = torch.zeros_like(input)
                # zero = F.pad(zero, [1, 1, 1, 1], value=1)
                mean, log_sd = self.prior(zero).chunk(2, 1)
                z = gaussian_sample(eps, mean, log_sd)
                input = z

        for flow in self.flows[::-1]:
            input = flow.reverse(input)

        b_size, n_channel, height, width = input.shape

        unsqueezed = input.view(b_size, n_channel // 4, 2, 2, height, width)
        unsqueezed = unsqueezed.permute(0, 1, 4, 2, 5, 3)
        unsqueezed = unsqueezed.contiguous().view(
            b_size, n_channel // 4, height * 2, width * 2
        )

        return unsqueezed

Glow

nn.ModuleList中定义了很多block

最后一层split设置成False

classifier_net通过MLP判别到正确的分类上

依次遍历block，送入block中得到out，det，log_p，z_new，统计zout，logdet，logpsum

送入classifier_net进行判别

reverse则依次调用

class Glow(nn.Module):
    def __init__(
        self, in_channel, n_flow, n_block, affine=True, conv_lu=True
    ):
        super().__init__()

        self.blocks = nn.ModuleList()
        n_channel = in_channel
        for i in range(n_block - 1):
            self.blocks.append(Block(n_channel, n_flow, affine=affine, conv_lu=conv_lu))
            n_channel *= 2
        self.blocks.append(Block(n_channel, n_flow, split=False, affine=affine))

    def forward(self, input):
        log_p_sum = 0
        logdet = 0
        out = input
        z_outs = []

        for block in self.blocks:
            out, det, log_p, z_new = block(out)
            z_outs.append(z_new)
            logdet = logdet + det

            if log_p is not None:
                log_p_sum = log_p_sum + log_p

        return log_p_sum, logdet, z_outs

    def reverse(self, z_list, reconstruct=False):
        for i, block in enumerate(self.blocks[::-1]):
            if i == 0:
                input = block.reverse(z_list[-1], z_list[-1], reconstruct=reconstruct)

            else:
                input = block.reverse(input, z_list[-(i + 1)], reconstruct=reconstruct)

        return input