记录：2022-9-19 螺旋矩阵 球会落何处 分页分区

学习时间：2022-9-19

学习内容

1、leetcode

54. 螺旋矩阵

这道题比想的要难做一些，主要方法有两种，一种是分层，一种是模拟，分层的思想，每次都走最外层，然后用top left right bottom记录，当top、bottom重合或left、right重合时，说明当前已经走到最后，否则top,left++,right\bottom–.
代码如下：

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    order.add(matrix[bottom][column]);
                }
                for (int row = bottom; row > top; row--) {
                    order.add(matrix[row][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

第二种解法是模拟，模拟这种移动方式，不停遍历，这种比较难写 没有写出来
这种解法需要用的visited数组，判断是否已经走过，如果走过 需要换方向
我死在了这个方向上，我构建的是一维数组，这个题解构建的二维数组，构建二维数组是因为方向是两个位置，我没有想到这一点，非常可惜

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        boolean[][] visited = new boolean[rows][columns];
        int total = rows * columns;
        int row = 0, column = 0;
        int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        int directionIndex = 0;
        for (int i = 0; i < total; i++) {
            order.add(matrix[row][column]);
            visited[row][column] = true;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
                directionIndex = (directionIndex + 1) % 4;
            }
            row += directions[directionIndex][0];
            column += directions[directionIndex][1];
        }
        return order;
    }
}

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/spiral-matrix/solution/luo-xuan-ju-zhen-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(mn)O(mn)，其中 mm 和 nn 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
空间复杂度：O(mn)O(mn)。需要创建一个大小为 m \times nm×n 的矩阵 \textit{visited}visited 记录每个位置是否被访问过。

1706. 球会落何处

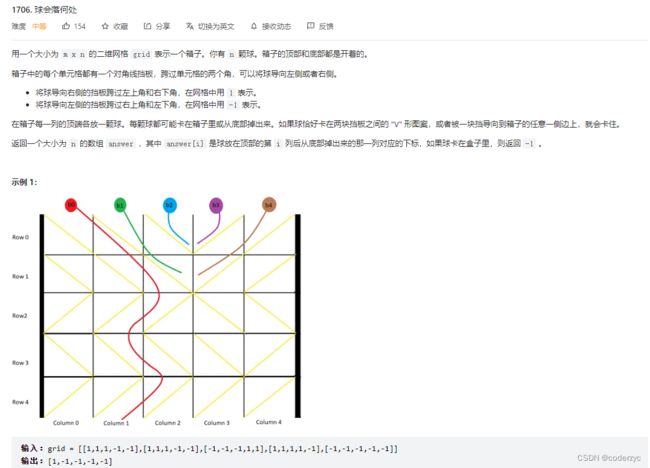
这道题其实属于一道找规律题，只要找到规律了就很好做
规律为：
碰到墙壁或者组成v，则说明无法到下面，否则一直执行，直到出去
如何才能不组成V呢，只需要x和他的下一位方向相同，就一定不会组成V，否则就会出现V
我没有用动态规划做这个题，但实际上也可以用dp，dp的每一位存储的j位置能到的column列

class Solution {
    public int[] findBall(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[] ans = new int[col];
        for(int i = 0;i<col;i++){
            int result = 1;
            //从i开始的球，是否可以放入
            //1 是否可以走下一步 若可以 标明下一步方向
            int x = i;
            for(int j = 0;j<row;j++){
                int nowdir = grid[j][x];
                //判断是否会碰壁
                if(x==0 && nowdir == -1){
                    result = -1;
                    break;
                }
                if(x==col-1 && nowdir == 1){
                    result = -1;
                    break;
                }
                //是否组成V
                if(nowdir != grid[j][x+nowdir]){
                    result = -1;
                    break;
                }
                x = x+nowdir;
            }
            if(result == 1){
                //看他掉在哪
                ans[i] = x;
            }else{
                ans[i] = -1;
            }
            
        }
        return ans;
    }
}

2、分页 分区

重新巩固分页和分区的概念
首先，为什么有分区？分区的意义是：需要给内存找到一个空闲的位置，然后通过文件系统将程序加载到这个空闲的位置，分区有两种，一种是可变分区，一种是固定分区，固定分区分配很容易出现不合理的情况（实现简单，只需要极少的操作系统开销），一般使用可变分区进行动态分配，可变分区有最佳分配 最先分配 最差分配 三种情况，现在从不同维度考虑这些分区方式的好坏

最佳分配

思路是找到最适合当前request内存的最小的内存空间
优点：当需要一个特别大的块时，这种分配方式可以拿出来
缺点：外部碎片多且小，不好解决

最先分配

分配找到的第一个大于request内存的空间
优点：特别快 O（1），均匀分配
缺点：这种分配会使得内存的低地址部分出现很多小的空闲分区，而每次分配查找时，都要经过这些分区，因此也增加了查找的开销

一般来说，这个算法是最好的

最差分配

查询所有内存空间中的最大块，并拿来分配
但是却把最大的连续内存划分开，会很快导致没有可用的大的内存块，因此性能也非常差

解决外部碎片的方法有合并紧缩，这种方式会导致死机现象的产生，所以性能消耗较大

由于上述这些分配方式并不能解决外部碎片的问题，所以需要引出分页的概念
分页让每次分配的内存按页为单位读入，这样不会产生外部碎片，只会产生内部碎片，而且每次的内部碎片不多，最大消耗为一个页的大小
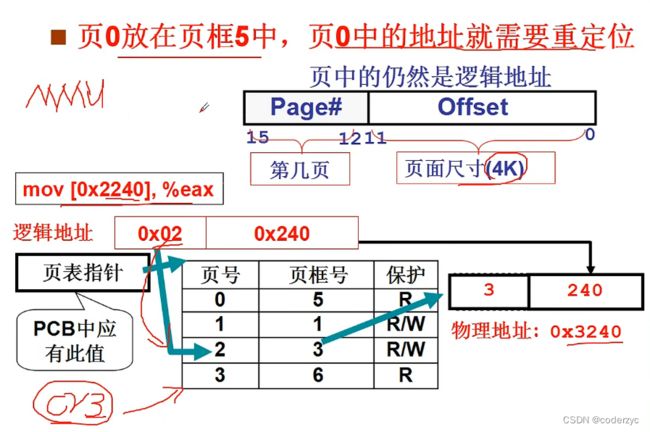
下图为一个从指令读取到物理地址的过程：

首先，输入mov [0x2240],%eax

这个地址的2240，由于每个页面4K(2¹² = 右移三位 因为一个数字类型占四位)，所以对应2240可以右移三位，2240>>3= 2，拆分为2 与 240，240为offset，在页号为2的位置，从PCB中找到页表，然后找到页框号为3的位置，并偏移240，得到物理地址0x3240，就实现了映射关系