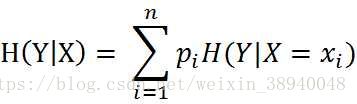用简单的数学公式理解决策树算法(python)
大家好,这是本居居第一次写博客。
希望以巩固自己的算法知识,以及用一种较为容易理解的方法阐述算法,让广大读者学习借鉴为目的,坚持写下去。
一、决策树算法定义:
百度的官方解释是这样的,决策树是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
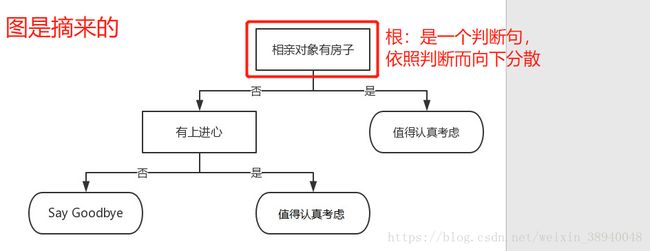
看不懂?难以理解?很迷惑?我也一样,我觉得可以先用一张图来初步认识决策树
我个人理解的决策树大概是这样的:
以根节点为起点,进行一次判断,由此一分为二,接着由二分四,以此类推,直到各节点无法继续分列
并且判断语句全是特征变量(即x),而每一个分支的终点则全是标签(即y)
二、构建决策树的准备工作
在说明之前,先抛出几个问题,并自问自答:
1、为什么根节点是判断 “相亲对象有房子” 这个特诊,而不是判断其他的特征?
答:决策树中特征变量的先后顺序的根据变量的"信息增益"来确定,哪个x的“信息增益大”,就用那一个X。
2、为什么在判断 相亲对象有房子 为 “是” 之后,就终结了,无法分列?而在判断 相亲对象有房子 为 “否” 之后却继续分列?
答:这个需要在X判断之后,考虑是否有继续分列的必要。
3、为什么用信息增益这个指标来构建决策树?
答:其实还可以用gini,信息增益比等,有兴趣的朋友可以多了解一下
上面提到了一个重要的知识点--“信息增益”,究竟什么是信息增益?并且如何计算信息增益?
在回答这两个问题前,需要补充另外两个知识点--“总体的经验熵(香农熵)”,“条件经验熵(香农熵)”
1)总体的经验熵公式如图
2)条件经验熵公式如图
是不是又看不懂?没关系,这时候直接看代码讲解计算(代码先截图)
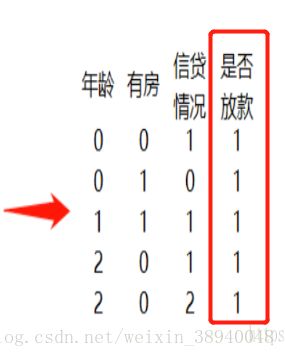
先创建数据集
计算总体经验熵
上图中红框的和 就是总体经验熵的计算公式,相比于 来说实例化更多,所用的就是一个简单的公式再求和。
来说实例化更多,所用的就是一个简单的公式再求和。
计算条件经验熵
条件经验熵是针对每个X而计算,上图是以年龄作为代表计算一次。
分别计算出年龄分组为0、1、2的条件经验熵,求和就是年龄的条件经验熵,即上图的红框部分求和。
条件经验熵与总体经验熵的公式类似,不同的在于条件经验熵需要乘以权重(权重即指每个分组占全部行数的占比)。
计算信息增益
到了这一步就很轻松了
X的信息增益=总体经验熵-X的条件经验熵,不要怀疑,就是这么简单,而代码只要短短几行遍可以搞定
所以,
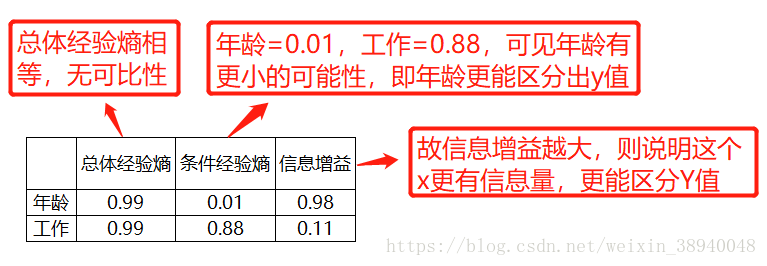
总体经验熵表示的是 y标签的不确定性,越大代表 y有更多的可能性。(不信你可以试试(0为1,1为14)以及(0为7,1为8)两类的总体经验熵哪边更大 )
条件经验熵表示的是 在某个x的条件下,y标签的不确定性,也是y对这个x的期望(这个从公式可以看出来)
而信息增益=总体经验熵-条件经验熵,表示的是这个X的信息量,值越大,说明这个X越重要(似乎难以理解,请看下图)
三、构建决策树算法步骤
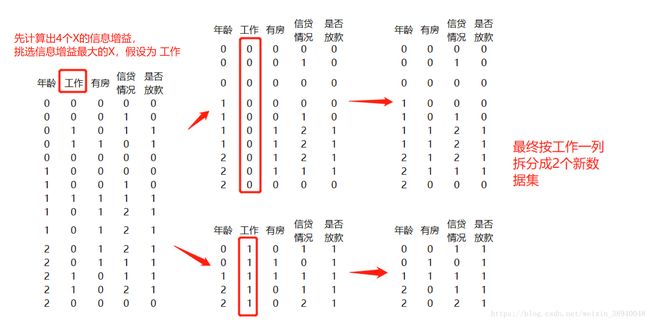
具体步骤:1、在数据集中计算出4个X的信息增益
2、挑选信息增益最大的X,然后按X的分组进行拆分数据集(例如工作则拆成3组,工作=0,1所对应的3个数据集),而信息增益最大的X将作为根进行判断。这里回答了上面第一个问题
3、依次在2个数据集中继续计算出其他X的信息增益
4、继续挑选信息增益最大的X,继续分组拆分,以此类推
以上步骤实际是一个递归循环,如图所示
接着以2个新的数据集继续递归循环,直到满足以下两个条件之一,便可以停止循环
第一个条件:拆分后的数据集,只有y,没有x;这种情况是属于无法继续拆分,此时取y的众数为叶;
第二个条件:拆分后的数据集,y列只有1个类别;例如在y全等于1的情况下,无论怎么拆分,y始终为1,那就没有继续拆分的必要了;例如上图中的第二个数据集
这里回答了上面的第二个问题。
四、构建决策树代码编写
五、可视化决策树
下图是最终的决策树可视化效果;
由于这部分代码都是抄来的,所以不进行讲解,有兴趣的可以看源代码或者下面的文献参考去查查。
六、用Sklearn 模块实现决策树算法
是不是有人好奇就这么几行代码就实现决策树+可视化了?
很高兴很明确告诉你,是的,就是这么简单
个人建议学习一个算法,需要清楚明了算法的真正原理、内在,而不是一味的迁徙代码,粘贴代码
每一个算法实现可能几行代码就轻松容易解决,但却是几代人的共同努力开发出来的
若看到这还理不清决策树打算直接用sklearn,希望你能重新再看一次,再理解一次
若你看了好几次还理不清,那。。多看看其他文章吧
七、总结
写到这里,其实也挺尴尬的。发现自己越写越懒,就连给所有图片取1234...名字都觉得累,不仅需要自己理解决策树算法,还需要能够讲得明了(这其实比自己理解算法更难)。很佩服那些写了几十篇,甚至几百几千篇博客的大神。
从一开始兴致勃勃打算以一种较为通俗幽默的风格写博客,到中间哑口无言不知怎么阐述观点,再到抱着能写完发表博客就行的态度慢慢转变。唉,就这样吧(叹气脸)。
希望有看到这里或者发现哪里有错误的人,有空的话麻烦评论下,怎么评论都行,让我看到有人来过,拜托了。
(如果能给出点中肯的建议那是再好不过了)
文献参考
1、https://blog.csdn.net/ling_mochen/article/details/80011263
谢谢大家
附上代码
from sklearn.model_selection import train_test_split
from pandas import DataFrame as df
from math import log
import pandas as pd
import operator
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
def createDataSet():
data = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
y_label="是否放款"
x_labels=["年龄","有工作","有自己的房子","信贷情况"]
return data,x_labels,y_label
def compute(x1,x2):
'''计算公式,这样写的原因是担心 当x1=0 或者x2-x1=0 时,log会报错,所以改成这样
'''
if x1==0:
return -(x2-x1)/x2*log((x2-x1)/x2,2)
if x2-x1==0:
return -x1/x2*log(x1/x2,2)
else:
return -x1/x2*log(x1/x2,2)-(x2-x1)/x2*log((x2-x1)/x2,2)
def calc_Hd(dataset):
# 计算总体H(D)
# all=统计总行数
all = dataset[y_label].count()
# 统计 y分别等于0、1的数量
calcEnt=df(dataset.groupby(y_label)[y_label].count())
# 计算 y分别等于0、1 的HD
calcEnt["Ent"]=calcEnt[y_label].apply(lambda x:-x/all*log(x/all,2))
# 计算总体的 HD
HD=round(calcEnt["Ent"].sum(),3)
print("总体经验熵:"+ str(HD))
return HD
def calc_Hyd(dataset,label):
'''计算条件熵 Hyd '''
# 该数据集 y 列 计数
all=dataset[y_label].count()
# 对 label 这个x 进行 分类计数
x_total = df(dataset.groupby(label)[label].count())
# 对 label 这个x 进行 分类计 y=1 的数
y_sum = df(dataset.groupby(label)[y_label].sum())
# 合并 上面所统计的计数 (即普通的连表操作)
x_total = df(pd.merge(x_total, y_sum, how="left", left_index=True, right_index=True))
# 计算 label 这个x 所有分类各自的 Hyd
x_total["Hyd"] = x_total.apply(lambda x: compute(x[y_label], x[label]) * x[label] / all, axis=1)
# 则 label 这个x 的 条件经验熵就是 所有分类各自的 Hyd 的总和
Hyd=round(x_total["Hyd"].sum(),3)
print(label + "的条件经验熵:" + str(Hyd))
return Hyd
def splitDataSet(dataSet, best_label, value):
# 根据信息增益最大的X 拆分数据集 的函数
redataSet=dataSet[dataSet[best_label].isin([value])]
redataSet=redataSet.drop(best_label,axis=1)
return redataSet
def majorityCnt(classList):
# 选取Y的众数的函数,这个函数是抄来的,毕竟懒
classCount = {}
for vote in classList: #统计classList中每个元素出现的次数
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
# 排序的字典 排序关键字为止,=order by 是否倒序
sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True) # 根据字典的值降序排序
return sortedClassCount[0][0] #返回classList中出现次数最多的元素
def createTree(x_labels,total):
classList = list(total[y_label]) # 取分类标签(是否放贷:yes or no)
if len(x_labels) == 0: # 若拆分后已经没有X 了,这返回y的众数 对应第一个条件
return majorityCnt(classList)
if len(set(classList)) == 1: # 若Y 只有一类 则返回, 对应第二个条件
return classList[0]
# 存储各个X 信息增益 的字典
Ent = {}
# 计算总体经验熵
HD = calc_Hd(total)
best_Ent = 0
best_label = ""
# 循环每个X 分别计算 条件经验熵,并将求得信息增益存储值Ent 字典中
for label in x_labels:
Hyd = calc_Hyd(total, label)
Ent[label] = round(HD - Hyd, 3)
# 循环判断 哪个X的信息增益最大
if Ent[label] >= best_Ent:
best_Ent = Ent[label]
best_label = label
x_labels.remove(best_label) # 删除已经使用特征标签
mytree={best_label:{}} # 用字段 构建决策树
featValues = set(total[best_label]) # 得到数据集中所有最优特征的属性值
for value in featValues:
mytree[best_label][value]=createTree(x_labels,splitDataSet(total,best_label,value))
return mytree
######################################################
######################################################
### 从这里起的函数为可视化决策树的函数,可忽略不看 ###
######################################################
######################################################
"""
函数说明:获取决策树叶子结点的数目
Parameters:
myTree - 决策树
Returns:
numLeafs - 决策树的叶子结点的数目
"""
def getNumLeafs(myTree):
numLeafs = 0 #初始化叶子
firstStr = next(iter(myTree)) #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
secondDict = myTree[firstStr] #获取下一组字典
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict': #测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
"""
函数说明:获取决策树的层数
Parameters:
myTree - 决策树
Returns:
maxDepth - 决策树的层数
"""
def getTreeDepth(myTree):
maxDepth = 0 #初始化决策树深度
firstStr = next(iter(myTree)) #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
secondDict = myTree[firstStr] #获取下一个字典
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict': #测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth #更新层数
return maxDepth
"""
函数说明:绘制结点
Parameters:
nodeTxt - 结点名
centerPt - 文本位置
parentPt - 标注的箭头位置
nodeType - 结点格式
Returns:
无
"""
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
arrow_args = dict(arrowstyle="<-") #定义箭头格式
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14) #设置中文字体
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', #绘制结点
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, FontProperties=font)
"""
函数说明:标注有向边属性值
Parameters:
cntrPt、parentPt - 用于计算标注位置
txtString - 标注的内容
Returns:
无
"""
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] #计算标注位置
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
"""
函数说明:绘制决策树
Parameters:
myTree - 决策树(字典)
parentPt - 标注的内容
nodeTxt - 结点名
Returns:
无
"""
def plotTree(myTree, parentPt, nodeTxt):
decisionNode = dict(boxstyle="sawtooth", fc="0.8") #设置结点格式
leafNode = dict(boxstyle="round4", fc="0.8") #设置叶结点格式
numLeafs = getNumLeafs(myTree) #获取决策树叶结点数目,决定了树的宽度
depth = getTreeDepth(myTree) #获取决策树层数
firstStr = next(iter(myTree)) #下个字典
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) #中心位置
plotMidText(cntrPt, parentPt, nodeTxt) #标注有向边属性值
plotNode(firstStr, cntrPt, parentPt, decisionNode) #绘制结点
secondDict = myTree[firstStr] #下一个字典,也就是继续绘制子结点
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD #y偏移
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict': #测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
plotTree(secondDict[key],cntrPt,str(key)) #不是叶结点,递归调用继续绘制
else: #如果是叶结点,绘制叶结点,并标注有向边属性值
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
"""
函数说明:创建绘制面板
Parameters:
inTree - 决策树(字典)
Returns:
无
"""
def createPlot(inTree):
fig = plt.figure(1, facecolor='white') #创建fig
fig.clf() #清空fig
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #去掉x、y轴
plotTree.totalW = float(getNumLeafs(inTree)) #获取决策树叶结点数目
plotTree.totalD = float(getTreeDepth(inTree)) #获取决策树层数
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0; #x偏移
plotTree(inTree, (0.5,1.0), '') #绘制决策树
plt.show() #显示绘制结果
"""
函数说明:使用决策树分类
Parameters:
inputTree - 已经生成的决策树
featLabels - 存储选择的最优特征标签
testVec - 测试数据列表,顺序对应最优特征标签
Returns:
classLabel - 分类结果
"""
def classify(inputTree, featLabels, testVec):
firstStr = next(iter(inputTree)) #获取决策树结点
secondDict = inputTree[firstStr] #下一个字典
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else: classLabel = secondDict[key]
return classLabel
if __name__ == '__main__':
data,x_labels,y_label=createDataSet()
x,y=[],[]
for i in data:
y.append(1 if i[-1]=="yes" else 0)
x.append(i[:-1])
train_x=df(x,columns=x_labels)
train_y=df(y,columns=[y_label])
total=df(pd.merge(train_x,train_y,how="left",left_index=True,right_index=True)) # 合并 X Y
mytree=createTree(x_labels,total)
print(mytree)
createPlot(mytree)
from sklearn.model_selection import train_test_split
from pandas import DataFrame as df
from math import log
import pandas as pd
import operator
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.externals.six import StringIO
from sklearn import tree #【tree 有两大函数 1、DecisionTreeClassifier--决策树构建 2、DecisionTreeRegressor --回归决策树 3、 export_graphviz --决策树可视化 参数参考https://blog.csdn.net/ling_mochen/article/details/80011263 】
import pydotplus
def createDataSet():
data = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
y_label="isOk"
x_labels=["age","work","house","credit"]
return data,x_labels,y_label
if __name__ == '__main__':
data,x_labels,y_label=createDataSet()
x,y=[],[]
for i in data:
y.append(i[-1])
x.append(i[:-1])
train_x=df(x,columns=x_labels)
train_y=df(y,columns=[y_label])
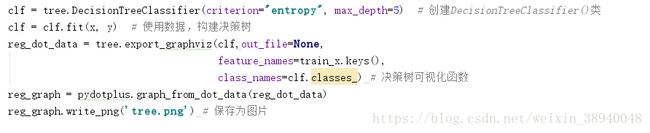
clf = tree.DecisionTreeClassifier(criterion="entropy", max_depth=5) # 创建DecisionTreeClassifier()类
clf = clf.fit(x, y) # 使用数据,构建决策树
reg_dot_data = tree.export_graphviz(clf,out_file=None,
feature_names=train_x.keys(),
class_names=clf.classes_) # 决策树可视化函数
reg_graph = pydotplus.graph_from_dot_data(reg_dot_data)
reg_graph.write_png('tree.png') # 保存为图片