Your Prediction Gets As Good As Your Data

Your Prediction Gets As Good As Your Data

May 5, 2015 by Kazem

In the past, we have seen software engineers and data scientists assume that they can keep increasing their prediction accuracy by improving their machine learning algorithm. Here, we want to approach the classification problem from a different angle where we recommend data scientists should analyze the distribution of their data first to measure information level in data. This approach can givesus an upper bound for how far one can improve the accuracy of a predictive algorithm and make sure our optimization efforts are not wasted!

Entropy and Information

In information theory, mathematician have developed a few useful techniques such as entropy to measure information level in data in process. Let's think of a random coin with a head probability of 1%.

If one filps such a coin, we will get more information when we see the head event since it's a rare event compared to tail which is more likely to happen. We can formualte the amount of information in a random variable with the negative logarithm of the event probability. This captures the described intuition. Mathmatician also formulated another measure called entropy by which they capture the average information in a random process in bits. Below we have shown the entropy formula for a discrete random variable:

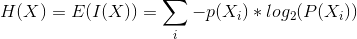
For the first example, let's assume we have a coin with P(H)=0% and P(T)=100%. We can compute the entropy of the coin as follows:

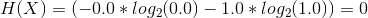
For the second example, let's consider a coin where P(H)=1% and P(T)=1-P(H)=99%. Plugging numbers one can find that the entropy of such a coin is:

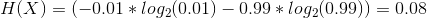
Finally, if the coin has P(H) = P(T) = 0.5 (i.e. a fair coin), its entropy is calculated as follows:

Entropy and Predictability

So, what these examples tell us? If we have a coin with head probability of zero, the coin's entropy is zero meaning that the average information in the coin is zero. This makes sense because flipping such a coin always comes as tail. Thus, the prediction accuracy is 100%. In other words, when the entropy is zero, we have the maximum predictibility.

In the second example, head probability is not zero but still very close to zero which again makes the coin to be very predictable with a low entropy.

Finally, in the last example we have 50/50 chance of seeing head/tail events which maximizes the entropy and consequently minimizes the predictability. In words, one can show that a fair coin has the meaximum entropy of 1 bit making the prediction as good as a random guess.

Kullback–Leibler divergence

As last example, it's important to give another example of how we can borrow ideas from information theory to measure the distance between two probability distributions. Let's assume we are modeling two random processes by their pmf's: P(.) and Q(.). One can use entropy measure to compute the distance between two pmf's as follows:

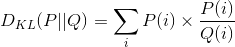
Above distance function is known as KL divergence which measures the distance of Q's pmf from P's pmf. The KL divergence can come handy in various problems such as NLP problems where we'd like to measure the distance between two sets of data (e.g. bag of words).

Wrap-up

In this post, we showed that the entropy from information theory provides a way to measure how much information exists in our data. We also highlighted the inverse relationship between the entropy and the predictability. This shows that we can use the entropy measure to calculate an upper bound for the accuracy of the prediction problem in hand.

Feel free to share with us if you have any comments or questions in the comment section below.

You can also reach us at [email protected]