【概率论基础进阶】数理统计的基本概念-常用统计分布
文章目录
-
- χ 2 \chi^{2} χ2分布
-
- 性质
- t t t分布
-
- 性质
- F F F分布
-
- 性质
- 正态总体的抽验分布
-
- 一个正态总体
- 两个正态总体
χ 2 \chi^{2} χ2分布
定义:设随机变量 X 1 , X 2 , ⋯ , X n X_{1},X_{2},\cdots,X_{n} X1,X2,⋯,Xn相互独立且均服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),则称随机变量
χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 \chi^{2}=X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2} χ2=X12+X22+⋯+Xn2
服从自由度为 n n n的 χ 2 \chi^{2} χ2分布,记作 χ 2 ∼ χ 2 ( n ) \chi^{2}\sim \chi^{2}(n) χ2∼χ2(n)
n n n个相互独立标准正态随机变量的平方和 χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 \chi^{2}=X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2} χ2=X12+X22+⋯+Xn2称为 χ 2 ( n ) \chi^{2}(n) χ2(n)的典型模式
性质
设 χ 2 ∼ χ 2 ( n ) \chi^{2}\sim \chi^{2}(n) χ2∼χ2(n),对给定 α ( 0 < α < 1 ) \alpha(0<\alpha<1) α(0<α<1),称满足条件
P { χ 2 > χ α 2 ( n ) } = ∫ χ α 2 ( n ) + ∞ f ( x ) d x = α P \left\{\chi^{2}> \chi^{2}_{\alpha}(n)\right\}=\int_{\chi_{\alpha}^{2}(n)}^{+\infty}f(x)dx=\alpha P{χ2>χα2(n)}=∫χα2(n)+∞f(x)dx=α
的点 χ α 2 ( n ) \chi^{2}_{\alpha}(n) χα2(n)为 χ 2 ( n ) \chi^{2}(n) χ2(n)分布的上 α \alpha α分位点,如下图所示
对不同的 α \alpha α和 n n n, χ α 2 \chi_{\alpha}^{2} χα2通常通过查表求得
设 χ 2 ∼ χ 2 ( n ) \chi^{2}\sim \chi^{2}(n) χ2∼χ2(n),则 E ( χ 2 ) = n , D ( χ 2 ) = 2 n E(\chi^{2})=n,D(\chi^{2})=2n E(χ2)=n,D(χ2)=2n
设 χ 1 2 ∼ χ 2 ( n 1 ) , χ 2 2 ∼ χ 2 ( n 2 ) \chi_{1}^{2}\sim \chi^{2}(n_{1}),\chi_{2}^{2}\sim \chi^{2}(n_{2}) χ12∼χ2(n1),χ22∼χ2(n2),且 χ 1 2 \chi_{1}^{2} χ12和 χ 2 2 \chi_{2}^{2} χ22相互独立,则 χ 1 2 + χ 2 2 ∼ χ 2 ( n 1 + n 2 ) \chi_{1}^{2}+\chi_{2}^{2}\sim \chi^{2}(n_{1}+n_{2}) χ12+χ22∼χ2(n1+n2)
例1:已知 χ 2 ∼ χ 2 ( n ) \chi^{2}\sim \chi^{2}(n) χ2∼χ2(n),则 E ( χ 4 ) = ( ) E(\chi^{4})=() E(χ4)=()
E ( χ 4 ) = D ( χ 2 ) + [ E ( χ 2 ) ] 2 = 2 n + n 2 E(\chi^{4})=D(\chi^{2})+[E(\chi^{2})]^{2}=2n+n^{2} E(χ4)=D(χ2)+[E(χ2)]2=2n+n2
t t t分布
定义:设随机变量 X X X和 Y Y Y相互独立,且 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X \sim N(0,1),Y \sim \chi^{2}(n) X∼N(0,1),Y∼χ2(n),则称随机变量服从自由度为 n n n的 t t t分布,记作 T ∼ t ( n ) T \sim t(n) T∼t(n)
满足 X , Y X,Y X,Y独立, X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X \sim N(0,1),Y \sim \chi^{2}(n) X∼N(0,1),Y∼χ2(n)三条件的 T = X Y / n T=\frac{X}{\sqrt{Y/n}} T=Y/nX称为 t ( n ) t(n) t(n)的典型模式
性质
t t t分布的概率密度 f ( x ) f(x) f(x)是偶函数,即
f ( x ) = f ( − x ) f(x)=f(-x) f(x)=f(−x)
且当 n n n充分大时, t ( n ) t(n) t(n)分布近似于 N ( 0 , 1 ) N(0,1) N(0,1)分布
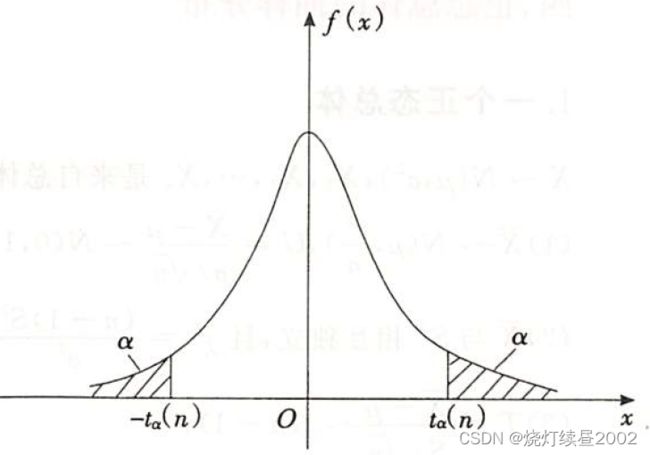
设 T ∼ t ( n ) T \sim t(n) T∼t(n),对给定的 α ( 0 < α < 1 ) \alpha(0<\alpha<1) α(0<α<1),称满足条件
P { T > t α ( n ) } = ∫ t α ( n ) + ∞ f ( x ) d x = α P \left\{T >t_{\alpha}(n)\right\}=\int_{t_{\alpha}(n)}^{+\infty}f(x)dx=\alpha P{T>tα(n)}=∫tα(n)+∞f(x)dx=α
的点 t α ( n ) t_{\alpha}(n) tα(n)为 t ( n ) t(n) t(n)分布的上 α \alpha α分位点
由于 t ( n ) t(n) t(n)分布的概率密度为偶函数,可知 t t t分布的双侧 α \alpha α分位点 t α / 2 ( n ) t_{\alpha/2}(n) tα/2(n),有
P { ∣ T ∣ > t α / 2 ( n ) } = α P \left\{|T|>t_{\alpha/2}(n)\right\}=\alpha P{∣T∣>tα/2(n)}=α
如图,由对称性可知
t 1 − α ( n ) = − t α ( n ) t_{1-\alpha}(n)=-t_{\alpha}(n) t1−α(n)=−tα(n)
F F F分布
定义:设随机变量 X X X和 Y Y Y相互独立,且 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) X \sim \chi^{2}(n_{1}),Y \sim \chi^{2}(n_{2}) X∼χ2(n1),Y∼χ2(n2),则称随机变量
F = X / n 1 Y / n 2 F=\frac{X/n_{1}}{Y/n_{2}} F=Y/n2X/n1
服从自由度为 ( n 1 , n 2 ) (n_{1},n_{2}) (n1,n2)的 F F F分布,记作 F ∼ F ( n 1 , n 2 ) F \sim F(n_{1},n_{2}) F∼F(n1,n2),其中 n 1 n_{1} n1和 n 2 n_{2} n2分别称为第一自由度和第二自由度
满足 X , Y X,Y X,Y独立, X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) X \sim \chi^{2}(n_{1}),Y \sim \chi^{2}(n_{2}) X∼χ2(n1),Y∼χ2(n2)三条件的 F = X / n 1 Y / n 2 \begin{aligned} F=\frac{X/n_{1}}{Y/n_{2}}\end{aligned} F=Y/n2X/n1称为 F ( n 1 , n 2 ) F(n_{1},n_{2}) F(n1,n2)的典型模式
性质
设 F ∼ F ( n 1 , n 2 ) F \sim F(n_{1},n_{2}) F∼F(n1,n2),对给定的 α ( 0 < α < 1 ) \alpha(0<\alpha<1) α(0<α<1),称满足条件
P { F > F α ( n 1 , n 2 ) } = ∫ F α ( n 1 , n 2 ) + ∞ f ( x ) d x = α P \left\{F>F_{\alpha}(n_{1},n_{2})\right\}=\int_{F_\alpha(n_{1},n_{2})}^{+\infty}f(x)dx=\alpha P{F>Fα(n1,n2)}=∫Fα(n1,n2)+∞f(x)dx=α
的点 F α ( n 1 , n 2 ) F_\alpha(n_{1},n_{2}) Fα(n1,n2)为 F ( n 1 , n 2 ) F(n_{1},n_{2}) F(n1,n2)分布的上 α \alpha α分位点
如果 F ∼ F ( n 1 , n 2 ) F \sim F(n_{1},n_{2}) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \begin{aligned} \frac{1}{F}\sim F(n_{2},n_{1})\end{aligned} F1∼F(n2,n1),且有
F 1 − α ( n 1 , n 2 ) = 1 F α ( n 2 , n 1 ) F_{1-\alpha}(n_{1},n_{2})=\frac{1}{F_{\alpha}(n_{2},n_{1})} F1−α(n1,n2)=Fα(n2,n1)1
证明:
1 − α = P { F > F 1 − α ( n 1 , n 2 ) } = P { 1 F < 1 F 1 − α ( n 1 , n 2 ) } = 1 − P { 1 F ≥ 1 F 1 − α ( n 1 , n 2 ) } = 1 − P { 1 F > 1 F 1 − α ( n 1 , n 2 ) } \begin{aligned} 1-\alpha&=P \left\{F>F_{1-\alpha}(n_{1},n_{2})\right\}\\ &=P\left\{ \frac{1}{F}< \frac{1}{F_{1-\alpha}(n_{1},n_{2})}\right\}\\ &=1-P\left\{ \frac{1}{F}\geq \frac{1}{F_{1-\alpha}(n_{1},n_{2})}\right\}\\ &=1-P\left\{ \frac{1}{F}> \frac{1}{F_{1-\alpha}(n_{1},n_{2})}\right\} \end{aligned} 1−α=P{F>F1−α(n1,n2)}=P{F1<F1−α(n1,n2)1}=1−P{F1≥F1−α(n1,n2)1}=1−P{F1>F1−α(n1,n2)1}
有 P { 1 F > 1 F 1 − α ( n 1 , n 2 ) } = α \begin{aligned} P\left\{ \frac{1}{F}> \frac{1}{F_{1-\alpha}(n_{1},n_{2})}\right\}=\alpha\end{aligned} P{F1>F1−α(n1,n2)1}=α,又根据 F F F分布的性质,有
P { 1 F > F α ( n 2 , n 1 ) } = α P \left\{ \frac{1}{F}>F_{\alpha}(n_{2},n_{1})\right\}=\alpha P{F1>Fα(n2,n1)}=α
因此 1 F 1 − α ( n 1 , n 2 ) = F α ( n 2 , n 1 ) \begin{aligned} \frac{1}{F_{1-\alpha}(n_{1},n_{2})}=F_{\alpha}(n_{2},n_{1})\end{aligned} F1−α(n1,n2)1=Fα(n2,n1)
正态总体的抽验分布
一个正态总体
X ∼ N ( μ , σ 2 ) , X 1 , X 2 , ⋯ , X n X \sim N(\mu,\sigma^{2}),X_{1},X_{2},\cdots,X_{n} X∼N(μ,σ2),X1,X2,⋯,Xn是来自总体的样本,样本均值为 X ˉ \bar{X} Xˉ,样本方差为 S 2 S^{2} S2,则有:
- X ˉ ∼ N ( μ , σ 2 n ) , U = X ˉ − μ σ / n ∼ N ( 0 , 1 ) \begin{aligned} \bar{X}\sim N(\mu, \frac{\sigma^{2}}{n}),U=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)\end{aligned} Xˉ∼N(μ,nσ2),U=σ/nXˉ−μ∼N(0,1)
- X ˉ \bar{X} Xˉ与 S 2 S^{2} S2相互独立,且 χ 2 = ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \begin{aligned} \chi^{2}=\frac{(n-1)S^{2}}{\sigma^{2}}\sim \chi^{2}(n-1)\end{aligned} χ2=σ2(n−1)S2∼χ2(n−1)
- T = X ˉ − μ σ / n / ( n − 1 ) S 2 σ 2 ( n − 1 ) = X ˉ − μ S / n ∼ t ( n − 1 ) \begin{aligned} T=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\Big/\sqrt{\frac{(n-1)S^{2}}{\sigma^{2}(n-1)}}=\frac{\bar{X}-\mu}{S/\sqrt{n}}\sim t(n-1)\end{aligned} T=σ/nXˉ−μ/σ2(n−1)(n−1)S2=S/nXˉ−μ∼t(n−1)
- χ 2 = 1 σ 2 ∑ i = 1 n ( X i − μ ) 2 ∼ χ 2 ( n ) \begin{aligned} \chi^{2}=\frac{1}{\sigma^{2}}\sum\limits_{i=1}^{n}(X_{i}-\mu)^{2}\sim \chi^{2}(n)\end{aligned} χ2=σ21i=1∑n(Xi−μ)2∼χ2(n)
两个正态总体
X ∼ N ( μ , σ 1 2 ) X \sim N(\mu,\sigma^{2}_{1}) X∼N(μ,σ12)和 Y ∼ N ( μ 2 , σ 2 2 ) , X 1 , X 2 , ⋯ , X n 1 Y \sim N(\mu_{2},\sigma_{2}^{2}),X_{1},X_{2},\cdots,X_{n_{1}} Y∼N(μ2,σ22),X1,X2,⋯,Xn1和 Y 1 , Y 2 , ⋯ , Y n 2 Y_{1},Y_{2},\cdots ,Y_{n_{2}} Y1,Y2,⋯,Yn2是分别来自总体 X X X和 Y Y Y的样本且相互独立,样本均值分别为 X ˉ \bar{X} Xˉ和 Y ˉ \bar{Y} Yˉ,样本方差分别为 S 1 2 S_{1}^{2} S12和 S 2 2 S_{2}^{2} S22,则有
- X ˉ − Y ˉ ∼ N ( μ 1 − μ 2 , σ 1 2 n 1 + σ 2 2 n 2 ) , U = ( X ˉ − Y ˉ ) − ( μ 1 − μ 2 ) σ 1 2 n 1 + σ 2 2 n 2 ∼ N ( 0 , 1 ) \begin{aligned} \bar{X}-\bar{Y}\sim N\left(\mu_{1}-\mu_{2}, \frac{\sigma_{1}^{2}}{n_{1}}+ \frac{\sigma_{2}^{2}}{n_{2}}\right),U=\frac{(\bar{X}-\bar{Y})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+ \frac{\sigma_{2}^{2}}{n_{2}}}}\sim N(0,1)\end{aligned} Xˉ−Yˉ∼N(μ1−μ2,n1σ12+n2σ22),U=n1σ12+n2σ22(Xˉ−Yˉ)−(μ1−μ2)∼N(0,1)
- 如果 σ 1 2 = σ 2 2 \sigma_{1}^{2}=\sigma_{2}^{2} σ12=σ22,则
T = X ˉ − Y ˉ − ( μ 1 − μ 2 ) S w 1 n 1 + 1 n 2 ∼ t ( n 1 + n 2 − 2 ) T=\frac{\bar{X}-\bar{Y}-(\mu_{1}-\mu_{2})}{S_{w}\sqrt{\frac{1}{n_{1}}+ \frac{1}{n_{2}}}}\sim t(n_{1}+n_{2}-2) T=Swn11+n21Xˉ−Yˉ−(μ1−μ2)∼t(n1+n2−2)
其中 S w 2 = ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 + n 2 − 2 \begin{aligned} S_{w}^{2}=\frac{(n_{1}-1)S_{1}^{2}+(n_{2}-1)S_{2}^{2}}{n_{1}+n_{2}-2}\end{aligned} Sw2=n1+n2−2(n1−1)S12+(n2−1)S22 - F = S 1 2 / σ 1 2 S 2 2 / σ 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) \begin{aligned} F=\frac{S_{1}^{2}/\sigma_{1}^{2}}{S_{2}^{2}/\sigma_{2}^{2}}\sim F(n_{1}-1,n_{2}-1)\end{aligned} F=S22/σ22S12/σ12∼F(n1−1,n2−1)
若 X X X与 Y Y Y相互独立 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) X \sim \chi^{2}(n_{1}),Y \sim \chi^{2}(n_{2}) X∼χ2(n1),Y∼χ2(n2),则
F = X / n 1 Y / n 2 ∼ F ( n 1 , n 2 ) F=\frac{X/n_{1}}{Y/n_{2}}\sim F(n_{1},n_{2}) F=Y/n2X/n1∼F(n1,n2)
称为自由度为 n 1 , n 2 n_{1},n_{2} n1,n2的 F F F分布
例1:设总体 X X X的概率密度 f ( x ) = 1 2 e − ∣ x ∣ , − ∞ < x < + ∞ , X 1 , X 2 , ⋯ , X n \begin{aligned} f(x)=\frac{1}{2}e^{-|x|},-\infty
E ( S 2 ) = D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 E X = ∫ − ∞ + ∞ x ⋅ 1 2 e − ∣ x ∣ d x = 0 E ( X 2 ) = ∫ − ∞ + ∞ x 2 ⋅ 1 2 e − ∣ x ∣ d x = 2 ∫ 0 + ∞ x 2 ⋅ 1 2 e − x d x = ∫ 0 + ∞ x 2 e − x d x = 2 \begin{aligned} E(S^{2})&=D(X)=E(X^{2})-[E(X)]^{2}\\ EX&=\int_{-\infty}^{+\infty}x \cdot \frac{1}{2}e^{-|x|}dx=0\\ E(X^{2})&=\int_{-\infty}^{+\infty}x^{2} \cdot \frac{1}{2}e^{-|x|}dx\\ &=2\int_{0}^{+\infty}x^{2} \cdot \frac{1}{2}e^{-x}dx\\ &=\int_{0}^{+\infty}x^{2}e^{-x}dx=2 \end{aligned} E(S2)EXE(X2)=D(X)=E(X2)−[E(X)]2=∫−∞+∞x⋅21e−∣x∣dx=0=∫−∞+∞x2⋅21e−∣x∣dx=2∫0+∞x2⋅21e−xdx=∫0+∞x2e−xdx=2
因此 E ( S 2 ) = 2 E(S^{2})=2 E(S2)=2
例2: X 1 , X 2 , X 3 , X 4 X_{1},X_{2},X_{3},X_{4} X1,X2,X3,X4为来自总体 N ( 1 , σ 2 ) ( σ > 0 ) N(1,\sigma^{2})(\sigma>0) N(1,σ2)(σ>0)的简单随机样本,证明统计量 X 1 − X 2 ∣ X 3 + X 4 − 2 ∣ ∼ t ( 1 ) \begin{aligned} \frac{X_{1}-X_{2}}{|X_{3}+X_{4}-2|}\sim t(1)\end{aligned} ∣X3+X4−2∣X1−X2∼t(1)
X 1 − X 2 ∼ N ( 0 , 2 σ 2 ) ⇒ X 1 − X 2 2 σ ∼ N ( 0 , 1 ) X 3 + X 4 − 2 ∼ N ( 0 , 2 σ 2 ) ⇒ X 3 + X 4 − 2 2 σ ∼ N ( 0 , 1 ) ⇒ ( X 3 + X 4 − 2 2 σ ) 2 ∼ χ 2 ( 1 ) \begin{aligned} X_{1}-X_{2}\sim N(0,2 \sigma^{2})&\Rightarrow \frac{X_{1}-X_{2}}{\sqrt{2}\sigma}\sim N(0,1)\\ X_{3}+X_{4}-2 \sim N(0,2\sigma^{2})&\Rightarrow \frac{X_{3}+X_{4}-2}{\sqrt{2}\sigma}\sim N(0,1)\\ &\Rightarrow \left(\frac{X_{3}+X_{4}-2}{\sqrt{2}\sigma}\right)^{2}\sim \chi^{2}(1) \end{aligned} X1−X2∼N(0,2σ2)X3+X4−2∼N(0,2σ2)⇒2σX1−X2∼N(0,1)⇒2σX3+X4−2∼N(0,1)⇒(2σX3+X4−2)2∼χ2(1)
X 1 − X 2 X_{1}-X_{2} X1−X2与 X 3 + X 4 − 2 X_{3}+X_{4}-2 X3+X4−2相互独立, X 1 − X 2 2 σ \begin{aligned} \frac{X_{1}-X_{2}}{\sqrt{2}\sigma}\end{aligned} 2σX1−X2与 ( X 3 + X 4 − 2 2 σ ) 2 \begin{aligned} \left(\frac{X_{3}+X_{4}-2}{\sqrt{2}\sigma}\right)^{2}\end{aligned} (2σX3+X4−2)2也相互独立,综上所述,记
X 1 − X 2 ∣ X 3 + X 4 − 2 ∣ = X 1 − X 2 2 σ ( X 3 + X 4 − 2 2 σ ) 2 / 1 = X Y / 1 \frac{X_{1}-X_{2}}{|X_{3}+X_{4}-2|}=\frac{\frac{X_{1}-X_{2}}{\sqrt{2}\sigma}}{\sqrt{\left(\frac{X_{3}+X_{4}-2}{\sqrt{2}\sigma}\right)^{2}/1}}=\frac{X}{\sqrt{Y/1}} ∣X3+X4−2∣X1−X2=(2σX3+X4−2)2/12σX1−X2=Y/1X
其中 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( 1 ) X \sim N(0,1),Y \sim \chi^{2}(1) X∼N(0,1),Y∼χ2(1),且 X X X与 Y Y Y相互独立,因此 X 1 − X 2 ∣ X 3 + X 4 − 2 ∣ ∼ t ( 1 ) \begin{aligned} \frac{X_{1}-X_{2}}{|X_{3}+X_{4}-2|}\sim t(1)\end{aligned} ∣X3+X4−2∣X1−X2∼t(1)
例3:设总体 X X X和 Y Y Y均服从正态分布 N ( μ , σ 2 ) , σ > 0 , X 1 , X 2 , ⋯ , X n N(\mu,\sigma^{2}),\sigma>0 ,X_{1},X_{2},\cdots,X_{n} N(μ,σ2),σ>0,X1,X2,⋯,Xn和 Y 1 , Y 2 , ⋯ , Y n Y_{1},Y_{2},\cdots ,Y_{n} Y1,Y2,⋯,Yn分别是来自总体 X X X和 Y Y Y的两个相互独立的简单随机样本,它们的样本方差分别为 S X 2 S^{2}_{X} SX2和 S Y 2 S_{Y}^{2} SY2,则统计量 T = n − 1 σ 2 ( S X 2 + S Y 2 ) \begin{aligned} T=\frac{n-1}{\sigma^{2}}(S_{X}^{2}+S_{Y}^{2})\end{aligned} T=σ2n−1(SX2+SY2)服从的分布及参数为()
n − 1 σ 2 S X 2 ∼ χ 2 ( n − 1 ) , n − 1 σ 2 S Y 2 ∼ χ 2 ( n − 1 ) \frac{n-1}{\sigma^{2}}S_{X}^{2}\sim \chi^{2}(n-1), \frac{n-1}{\sigma^{2}}S_{Y}^{2}\sim \chi^{2}(n-1) σ2n−1SX2∼χ2(n−1),σ2n−1SY2∼χ2(n−1)
又因为它们相互独立,故
n − 1 σ 2 S X 2 + n − 1 σ 2 S Y 2 = n − 1 σ 2 ( S X 2 + S Y 2 ) ∼ χ 2 ( 2 n − 2 ) \frac{n-1}{\sigma^{2}}S_{X}^{2}+\frac{n-1}{\sigma^{2}}S_{Y}^{2}=\frac{n-1}{\sigma^{2}}(S_{X}^{2}+S_{Y}^{2})\sim \chi^{2}(2n-2) σ2n−1SX2+σ2n−1SY2=σ2n−1(SX2+SY2)∼χ2(2n−2)
例9:设随机变量 X ∼ t ( n ) , Y ∼ F ( 1 , n ) X \sim t(n),Y \sim F(1,n) X∼t(n),Y∼F(1,n),给定 α ( 0 < α < 0.5 ) \alpha(0<\alpha<0.5) α(0<α<0.5),常数 c c c满足 P { X > c } = a P \left\{X>c\right\}=a P{X>c}=a,则 P { Y > c 2 } = ( ) P \left\{Y>c^{2}\right\}=() P{Y>c2}=()
X = X 1 Y 1 / n , 其中 X 1 ∼ N ( 0 , 1 ) ; Y 1 ∼ χ 2 ( n ) ; 二者相互独立 X=\frac{X_{1}}{\sqrt{Y_{1}/n}},其中X_{1}\sim N(0,1);Y_{1}\sim \chi^{2}(n);二者相互独立 X=Y1/nX1,其中X1∼N(0,1);Y1∼χ2(n);二者相互独立
因为 t t t分布的密度函数是偶函数,所以对给定的 α \alpha α,常数 c c c满足 P { X > c } = P { X < − c } = a P \left\{X>c\right\}=P \left\{X<-c\right\}=a P{X>c}=P{X<−c}=a。又有
X 2 = X 1 2 Y 1 / n , 其中 X 1 2 ∼ χ 2 ( 1 ) ; Y 1 2 ∼ χ 2 ( n ) ; 二者相互独立 X^{2}=\frac{X_{1}^{2}}{Y_{1}/n},其中X_{1}^{2}\sim \chi^{2}(1);Y_{1}^{2}\sim \chi^{2}(n);二者相互独立 X2=Y1/nX12,其中X12∼χ2(1);Y12∼χ2(n);二者相互独立
因此 X 2 ∼ F ( 1 , n ) X^{2}\sim F(1,n) X2∼F(1,n),因此有
P { Y > c 2 } = P { X 2 > c 2 } = P { X > c } + P { X < − c } = 2 α P \left\{Y>c^{2}\right\}=P \left\{X^{2}>c^{2}\right\}=P \left\{X>c\right\}+P \left\{X<-c\right\}=2 \alpha P{Y>c2}=P{X2>c2}=P{X>c}+P{X<−c}=2α
CSDN话题挑战赛第2期
参赛话题:学习笔记