基于梯度的轨迹优化(GTO)和拓扑路径搜索的路径引导的无人机(UAV)轨迹再规划(PGO)
文章目录
- 0 概览
- 1 关键问题
- 2 相关工作
-
- 2.1 基于梯度的轨迹优化
- 2.2 拓扑路径规划
-
- 2.2.1 等价关系
- 2.2.2 拓扑路线图
- 2.2.3 拓扑路线图伪代码
- 2.3 路径引导的轨迹优化( P G O PGO PGO)
-
- 2.3.1 优化失效
- 2.3.2 P G O PGO PGO实现
- 2.4 剪枝
- 2.5 实时拓扑轨迹重新规划
- 3 总结
0 概览
基于梯度的轨迹优化 G T O GTO GTO在四旋翼飞行器的轨迹重新规划中得到了广泛的应用,但是它存在局部极小值,这不仅对安全是致命的,而且不利于航行的顺利进行。此文章提出了一种基于 G T O GTO GTO的再规划方法,系统地解决了这一问题。针对不可行的局部极小点,提出了一种路径引导优化 P G O PGO PGO方法,大大提高了重规划的成功率。并提出了一种拓扑路径搜索算法,用于捕获三维环境中不同的有用路径集合,每条路径引导一个独立的轨迹优化。它激活了对解决方案空间的更全面的探索,并输出了更优的重新规划的轨迹。
- 因为是路径引导来进行对轨迹的优化,那么引导路径从哪里来呢?这就要用到拓扑路径搜索算法,这个算法来捕获三维环境当中不同的游泳路径集合,每条路径引导一个独立的轨迹进行优化
1 关键问题
- G T O GTO GTO通常将轨迹重新规划表述为一个非线性优化问题,在平滑性、安全性和动态可行性之间进行权衡,对于这个问题特别有效。由于它可以方便地将不可行的轨迹段变形为可行的轨迹段,并且具有非常高的效率和低内存需求,因此得到了广泛的应用。但基于 GTO 的重新规划仍受到局部最小值问题的困扰 ,问题源自优化的碰撞成本,应该根据环境的结构进行评估。由于存在多个安全和不安全区域,因此该成本本质上是非凸的,这个问题可能会导致致命的崩溃,因为它经常使轨迹陷入不可行的局部最小值并导致重新规划失败。此外,它还导致缺乏最优性保证,因为只搜索了初始轨迹周围的一小部分解空间。因此,所谓的局部最优轨迹通常不能满足平稳和安全的飞行。已经意识到这个关键问题,并采用随机重启和迭代细化等策略来缓解它。尽管如此,这个问题并没有从根本上解决,并且禁止将 GTO 应用于更具挑战性的场景,例如攻击性( a g g r e s s i v e aggressive aggressive)飞行
- 为了解决陷入局部最小值这个问题,通过一种新的基于 G T O GTO GTO的重新规划方法进行系统地解决
- 该方法包括路径引导优化( P G O PGO PGO)、发现拓扑不同路径的有效算法以及由路径引导的并行轨迹优化
- 提出了一种有效的基于采样的拓扑路径搜索方法来提取一组全面的路径来捕获环境的结构
2 相关工作
2.1 基于梯度的轨迹优化
-
G T O GTO GTO方法,是一种主要的路径生成算法,并把路径生成看作是一个最小化目标函数的非线性优化问题,但是也有一些小问题,就是局部最小值
-
P G O PGO PGO方法,在优化的过程当中加入几何路径,由于路径有效地引导优化逃离不可行的局部最小值,才保证了规划的成功率
-
同时,拓扑路径搜索产生的多条不同路径与 P G O PGO PGO集成
2.2 拓扑路径规划
2.2.1 等价关系
- 因为 P G O PGO PGO是路径引导轨迹优化,顾名思义就是要有一组路径进行引导,那拿什么路径进行引导呢?在这里提出了一种基于采样的拓扑路径搜索方法来寻找一组路径从而指导 P G O PGO PGO(关键,这组拓扑路径能够实时生成)
- 原有的可见性变形 V D VD VD 的计算量很大,所以使用统一参数化之后的可见性变形 U V D UVD UVD,更加有效地进行等价性验证
可见性变形:两条起点终点相同的轨迹,两者之间无障碍物且连线无碰撞,就代表可见,但是形状可以不相同。
等价性检查: V D VD VD 的计算代价很高,应该计算一个可见性图,并在其中进行路径搜索,这比检验 U V D UVD UVD 的复杂性更高。
- U V D UVD UVD 的定义:由下图可以看出,统一参数化的可见性变形,任何两个关联点在 U V D UVD UVD当中都对应着相同的参数 s s s( s ∈ [ 0 , 1 ] s∈[0,1] s∈[0,1]参数化),但是在 V D VD VD当中不对应,同时连接这两个点的线要无碰撞的,这才属于均匀的可见性变形(不同形) U V D UVD UVD类
- 蓝色与绿色之间线段发生碰撞,所以这不是 U V D UVD UVD类,蓝色与紫色同属于 U V D UVD UVD类,这就排除了一堆冗余的轨迹,削弱了轨迹的重复性,降低了计算复杂度
2.2.2 拓扑路线图
- 看最后一个轨迹图,红色和橙/黄色的路径都属于同一个 U V D UVD UVD类,而粉色路径是另外的一个 U V D UVD UVD类当中的唯一成员,因为除了粉色路径再也没有一条和粉色一样满足以上条件的轨迹了,所以粉色这个 U V D UVD UVD类就只有粉色这一条,而红色和黄色则属于另一个 U V D UVD UVD类,他们类下有红黄这两个成员
- 设计过程当中,引入了两种不同的图节点,分别是 g u a r d guard guard 守卫/警卫点,以及 c o n n e c t o r connector connector 连接点,类似于可视的概率路线图 V i s i b i l i t y − P R M Visibility-PRM Visibility−PRM, g u a r d guard guard 负责探索自由空间的未探索部分,任何两个 g u a r d guard guard 点 g 1 g_1 g1 和 g 2 g_2 g2 彼此之间都是不可见的,但是连接 g 1 g_1 g1 和 g 2 g_2 g2 的线段存在碰撞。每次在地图上采样一个点,如果这个点和另外的任何一个 g u a r d guard guard 都看不到,那么就把这个点记作一个新的 g u a r d guard guard 点。然后接着继续采样,如果一个采样点刚好可以被两个 g u a r d guard guard 看到,那么就把这个点记作 c o n n e c t o r connector connector,然后把这个 c o n n e c t o r connector connector 和这两个 g u a r d guard guard 点连接起来,连接好以后做两个事:如果这是一条全新的拓扑路径,那么就保留,否则判断两条拓扑路径的长度,把长的去掉,短的留下,保证最优性。
2.2.3 拓扑路线图伪代码
AddGuard(G, g):增加 g u a r d guard guard 节点到 G G G 中sample():采样节点VisibleGuard(G, Ps):得到 G G G 中能观测到 P s P_s Ps 的所有节点.size():计算节点的的个数Path(g1, c, g2):将 c o n n e c t o r connector connector 与 两个 g u a r d guard guard 之间生成路径SharedNeighbors(G,g1,g2):从 G G G 当中提取能够与 g 1 、 g 2 g_1、g_2 g1、g2连接的连接点集Equivalent(p1,p2):判断拓扑连接是是否相同len(p):计算路径长度Replace(G,p,n):替换 c o n n e c t o r connector connector 点( p p p换下 n n n)distinct:bool型数据, t r u e true true 表示拓扑连接有差别, f a l s e false false 表示拓扑连接无差别- t m a x t_{max} tmax:时间限制
- N m a x N_{max} Nmax:采样点个数限制
- G G G:所有 g u a r d guard guard 点以及 c o n n e c t o r connector connector 点的集合
-
伪代码说明:在设计拓扑路径图中,我们引入了两种不同的图节点,即 g u a r d guard guard 守卫/警卫点和 c o n n e c t o r connector connector连接点,类似于 V i s i b i l i t y − P R M Visibility-PRM Visibility−PRM。 g u a r d guard guard 负责探索自由空间的不同部分,任何两个 g u a r d guard guard,任何两个 g u a r d guard guard 点 g 1 g_1 g1 和 g 2 g_2 g2 彼此之间都是不可见的,但是连接 g 1 g_1 g1 和 g 2 g_2 g2 的线段存在碰撞。
-
在主循环之前,在起始点和结束点创建两个 g u a r d guard guard 点。每当采样点对所有其他 g u a r d guard guard 都不可见时,就会在此点创建一个新的 g u a r d guard guard 点,如第 6 − 7 6-7 6−7行。为了形成路线图的路径,使用连接点 c o n n e c t o r connector connector 连接不同的 g u a r d guard guard如第 7 − 19 7 -19 7−19行。当采样点恰好对两个 g u a r d guard guard可见时,就会创建一个新 c o n n e c t o r connector connector 点,要么连接 g u a r d guard guard,以形成拓扑上不同的连接第 19 − 20 19 - 20 19−20行,要么替换现有 c o n n e c t o r connector connector 以创建更短的路径第 16 − 17 16-17 16−17行。设置时间限制 t m a x t_{max} tmax或采样次数限制 N m a x N_{max} Nmax来终止循环。
-
下两图给出了属于两个UVD类别的三个轨迹的示例。下图2描述了VD和UVD之间的关系。它们都定义了两条路径 τ 1 ( s ) τ_1(s) τ1(s)和 τ 2 ( s ) τ_2(s) τ2(s)之间的连续映射,其中 τ 1 ( s ) τ_1(s) τ1(s)上的点通过直线变换到 τ 2 ( s ) τ_2(s) τ2(s)上的点。主要区别在于,对于UVD,点 τ 1 ( s 1 ) τ_1(s_1) τ1(s1)被映射到 τ 2 ( s 2 ) τ_2(s_2) τ2(s2),其中 s 1 = s 2 s_1=s_2 s1=s2,而对于VD, s 1 s_1 s1不必等于 s 2 s_2 s2。在概念上,UVD不那么通用,它描述了VD类的子集。实际上,它捕获的不同路径的类别比VD略多,但用于等价检查的成本要低得多
-
为了检验UVD的关系,把 s ∈ [ 0 , 1 ] s∈[0,1] s∈[0,1]均匀离散为 s i = i / K , i ∈ [ 0 , K ] s_i = i / K, i ∈[0,K] si=i/K,i∈[0,K]并检查 τ 1 ( s i ) τ_1(s_i) τ1(si)和 τ 2 ( s i ) τ_2(s_i) τ2(si)的冲突,对于分段直线路径,使除了 τ ( s ) τ(s) τ(s)以外的任何 s s s都是两条直线的交点
- UVD的一个例证,蓝色弹道与绿色弹道截然不同,但与紫色弹道相当。
- 综上,拓扑路径规划的复杂度过高,并基于此做出改进
2.3 路径引导的轨迹优化( P G O PGO PGO)
2.3.1 优化失效
- G T O GTO GTO的失败与质量不高/不利的初始化轨迹有关,就是以某些方式穿过障碍物的这一条初始路径通常会被卡住
- 典型的 GTO 方法将欧几里德符号距离场 (ESDF) 的梯度结合到碰撞成本中,以将轨迹推出障碍物,注意是将 E S D F ESDF ESDF的梯度结合到碰撞成本当中,这样才能将轨迹推出障碍物
- 此时改进的成本函数,该成本与平滑度和动态可行性成本相结合,形成一个目标函数,其梯度迭代地将轨迹变形为平稳平滑且安全的轨迹
- 在 E S D F ESDF ESDF 中存在一些“谷”或“脊”,其周围的梯度差异很大。因此,如果轨迹发生碰撞并穿过这些区域,则 ESDF 的梯度将在某些点突然变化。这可能导致目标函数的梯度将轨迹的不同部分推向相反的方向,从而导致优化失败
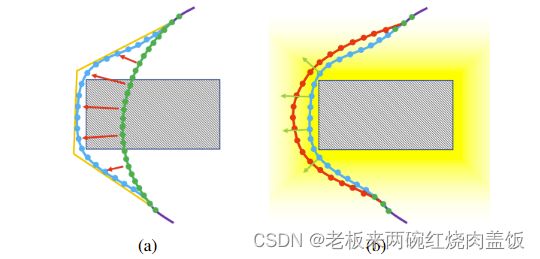
- 此为 G T O GTO GTO优化失败的例子
- 可以看出,当轨迹(绿色)穿过 E S D F ESDF ESDF用橙色虚线表示的“谷”(如图 ( a ) (a) (a))或者“脊”(如图 ( b ) (b) (b))时,轨迹的相邻部分会被推向相反的方向,黄色箭头表示目标函数的梯度,红色箭头表示 E S D F ESDF ESDF的梯度,这个目标函数就是上面所说的:该成本与平滑度和动态可行性成本相结合, 形成一个目标函数
- 通常,对于这样的“谷”和“脊”,对应于与附近障碍物表面具有相同距离的空间,是难以避免的,尤其是在复杂环境中。因此,仅依赖 E S D F ESDF ESDF 的优化有时不可避免地会失败。为了解决这个问题,必须引入额外的信息,这些信息可以产生一个目标函数,其梯度一致地将轨迹变形到自由空间
2.3.2 P G O PGO PGO实现
- P G O PGO PGO方法是基于 G T O GTO GTO的,只是在其上面做了一些改进, P G O PGO PGO的轨迹更换为 B B B 样条进行表示
- 对于 P G O PGO PGO方法,分为两个步骤:
- 产生一个过渡的中间热身轨迹( w a r m u p warmup warmup t r a j e c t o r y trajectory trajectory)(参考传统方法,比如 A ∗ A* A∗, R R T ∗ RRT* RRT∗这种基于采样的拓扑路径搜索方法,很容易找出没有碰撞的轨迹)
- 对这个 w a r m u p warmup warmup t r a j e c t o r y trajectory trajectory的平滑度以及与障碍物之间的间隙值进行再优化,如下图
- 如上图用于轨迹重新规划 P G O PGO PGO
- 如上图( a a a)第一阶段,几何引导路径(橙色线段)将原始 B B B样条轨迹(绿色)吸引到没有碰撞的自由空间当中形成 w a r m u p warmup warmup t r a j e c t o r y trajectory trajectory(蓝色);( b b b)图第二阶段将 w a r m u p warmup warmup t r a j e c t o r y trajectory trajectory在 E S D F ESDF ESDF中进一步进行优化,以提高轨迹的平滑性和间隙值以及与障碍物之间的优化,得到了红色的最终轨迹。前面也说了,这个几何引导轨迹通过 A ∗ A* A∗以及 R R T ∗ RRT* RRT∗等算法就可以得到,但是本文使用了拓扑路径搜索,其实都一样
-
第一阶段的优化目标函数为:综上这就是之前所说的目标函数。
f p 1 = λ 1 s f s + λ 1 g f g f_{p 1}=\lambda_{1 s} f_s+\lambda_{1 g} f_g fp1=λ1sfs+λ1gfg -
这里的 f s f_s fs是轨迹平滑性的惩罚函数,而 f g f_g fg 是引导路径和 B B B样条轨迹之间的距离的惩罚代价,主要是利用模拟弹性力来构造惩罚函数,其中 Q i Q_i Qi 为 B B B 样条轨迹的控制点,每个控制点 Q i Q_i Qi 都被分配了一个引导路径上关联的点 G i G_i Gi ,其由沿着引导路径进行均匀采样得到:
f s = ∑ i = p b − 1 N − p b + 1 ∥ Q i + 1 − 2 Q i + Q i − 1 ∥ 2 f_s=\sum_{i=p_b-1}^{N-p_b+1}\left\|\mathbf{Q}_{i+1}-2 \mathbf{Q}_i+\mathbf{Q}_{i-1}\right\|^2 fs=i=pb−1∑N−pb+1∥Qi+1−2Qi+Qi−1∥2
f g = ∑ i = p b N − p b ∥ Q i − G i ∥ 2 f_g=\sum_{i=p_b}^{N-p_b}\left\|\mathbf{Q}_i-\mathbf{G}_i\right\|^2 fg=i=pb∑N−pb∥Qi−Gi∥2 -
第二阶段的目标函数如下,其中 f s f_s fs 还是轨迹平滑性惩罚成本函数, f c f_c fc 是在 E S D F ESDF ESDF 上评估的碰撞成本函数,当轨迹接近障碍物时, E S D F ESDF ESDF的碰撞成本迅速增长。再利用惩罚函数 f v f_v fv 与 f a f_a fa 对 速度以及加速度的不可行程度进行量化,可以参考一下 m i n i m u m minimum minimum s n a p snap snap以及软硬约束的思想
f p 2 = λ 2 s f s + λ 2 c f c + λ 2 d ( f v + f a ) f_{p 2}=\lambda_{2 s} f_s+\lambda_{2 c} f_c+\lambda_{2 d}\left(f_v+f_a\right) fp2=λ2sfs+λ2cfc+λ2d(fv+fa) -
将轨迹表示为 B B B 样条,以实现更有效的成本评估,对于碰撞中的轨迹段,我们将其重新参数化为具有控制点 ( Q 0 , Q 1 , . . . , Q N ) {(Q_0, Q_1, ..., Q_N)} (Q0,Q1,...,QN)的 p b p_b pb次的均匀 B B B 样条(由于轨迹的边界状态约束,只有控制点的子集 ( Q p b , Q p b + 1 , ⋅ ⋅ ⋅ , Q N − p b ) {(Q_{pb},Q_{pb+1},···,Q_{N−pb})} (Qpb,Qpb+1,⋅⋅⋅,QN−pb)被优化。评价光滑度需要 Q p b − 2 、 Q p b − 1 、 Q N − p b + 1 和 Q N − p b + 2 {Q_{pb−2}、Q_{pb−1}、Q_{N−pb+1}和Q_{N−pb+2}} Qpb−2、Qpb−1、QN−pb+1和QN−pb+2。)
-
P G O PGO PGO 是由两个阶段组成的,第一段是产生一个中间的“热身轨迹”( w a r m u p warmup warmup t r a j e c t o r y trajectory trajectory)(如上图的那条绿色轨迹,原始的 B B B样条轨迹,以及使 B B B样条轨迹有效变形的外部信息,因为仅仅是应用 E S D F ESDF ESDF会是徒劳的)
2.4 剪枝
- 对于这条轨迹,可能会绕行,这样的路径是不利的,因为在PGO的第一阶段,它可能会使轨迹过度变形,使其不平滑。算法2的深度优先搜索,为找到的每个 P τ P_τ Pτ找到拓扑等价的捷径 P s P_s Ps(如上图所示)。该算法将 P τ P_τ Pτ均匀地离散为一组点 P d P_d Pd。在每次迭代中,如果 P d P_d Pd中的一个点 p d p_d pd从 P s P_s Ps中的最后一点看是不可见的(算法第3行,第4行),则找到阻挡 P s . b a c k ( ) P_s.back() Ps.back()视图的第一个被占用体素的中心(代码第5行)。然后,在与 l d l_d ld垂直并与 p b p_b pb处的ESDF梯度共面的方向上将该点推离障碍物(代码第6行),然后将其附加到 p s p_s ps(第7行)。这一过程一直持续到到达最后一点。
- 虽然在算法 1 中,避免了两个警卫之间的冗余连接,但在 s s s 和 g g g 之间可能存在少量冗余路径。为了完全排除重复的路径,我们检查任意两条路径之间的等价性,并且只保留拓扑不同的路径。
2.5 实时拓扑轨迹重新规划
- 上方的算法输出了一组富有成效的路径,可以指导轨迹优化。我们将它们与 P G O PGO PGO 适当地集成以进行实时重新规划,如图下所示。
- 在飞行过程中,会定期检查特定视野内的一段轨迹的安全性。一旦检测到碰撞,就会在立方体内触发拓扑路线图构建,这由段的开始和结束位置以及 ( r x , r y , r z ) (r_x, r_y, r_z) (rx,ry,rz)指定立方体的大小决定。从路线图中提取的路径被缩短和修剪,之后每条路径都会调用一个独立的 P G O PGO PGO。值得注意的是,替代 U V D UVD UVD 类别的数量随着障碍物的数量呈指数增长。因此,在复杂的环境中,可能难以针对所有路径进行优化。出于这个原因,我们只选择第一个 K m a x K_{max} Kmax 最短路径。比最短路径长 r m a x r_{max} rmax 倍的路径也被排除在外。这种策略限制了复杂性并且不会导致潜在最优性的缺失,因为非常长的路径不太可能产生最优轨迹。实际上,我们发现 K m a x = 5 K_{max}= 5 Kmax=5 就足够了。
3 总结
在本文中,提出了一种用于自主四旋翼导航的鲁棒轨迹重新规划方法。它通过路径引导优化、拓扑路径搜索和并行轨迹优化来克服局部最小值。进行了广泛的基准比较和积极的自主飞行实验,以验证方法的鲁棒性。目前,拓扑路径搜索的性能令人满意,但其完整性没有详细分析。此外,对重新规划方法的理论最优性并不完全确定。