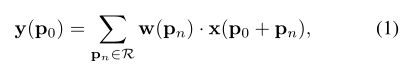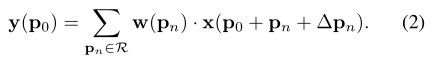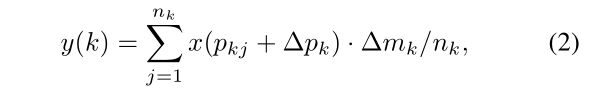Deformable Convolutional Networks——v1 and v2，可变形卷积
V1：Deformable Convolutional Networks
V2：Deformable ConvNets v2: More Deformable, Better Results
V1：
卷积神经网络（CNNs）由于卷积核固定的几何结构（常见的 1x1、3x3 和 5x5 等），导致其不能够很好地建模存在几何形变（geometric transformations）的物体。本文提出了两个可以用于提高 CNNs 建模几何形变能力的模块——deformable convolution 和 deformable RoI pooling ，两种模块都是通过在目标任务中学习偏移量（offsets）来改变空间中的采样位置。
从下面的图 1 中，可以看出标准卷积（standard convolutions）和可变形卷积（deformable convolutions）之间的区别。图（a）是一个常用的 3x3 的标准卷积所对应的采样点（绿色点）。图（b）是一个可变形卷积所对应的采样点（蓝色点），其中的箭头就是本文需要学习的偏移量（offsets），根据这些偏移量，就可以把标准卷积中对应的采样点（ 图(a)中绿色 ）移动到可变形卷积中的不规则采样点处（ 图(b)中蓝色 ）。图（c）和图（d）是图（b）的特殊情况，表明了可变形卷积囊括了长宽比、尺度变换和旋转变换。
一、Deformable Convolution（可变形卷积）
在标准卷积（standard convolution）中，对于输出特征图 
上的每一个点 
，它的计算如下：
其中：
为每一个采样点所对应的权重（也就是卷积核里的权重参数），对于一个常见的 3x3 的卷积核，
为：
即 
是以 
为中心点的 3x3 的小正方形。
可变形卷积在标准卷积中的每一个采样点位置上都加了一个可学习的偏置
，其表达式如下：
当 是一个分数时，采用 bilinear interpolation 计算 
的值，即：
上式中 
为分数（
）， 
为 
中所有是整数位置的点，实际上就只用到了 
周围的四个整数点（其余的点 g = 0）。式（4）将 
拆成了 维度和 维度上的线性插值的乘积。
可变形卷积（deformable convolution）的结构如下面 Fig 2 所示：上面那条支路通过一个卷积层用来学习偏移量（offsets）的大小，其中 offset field 的通道数（channel）为 2N，N 是卷积核的大小（如 3x3 的卷积核，N = 9），2N 是因为 output feature map 中的每一个点需要 N 个 ，而 是二维的，需要用两个数表示，如（0.5，-0.5）。
二、Deformable RoI Pooling（可变形的感兴趣区域池化）
1、RoI Pooling：也就是对一块感兴趣的区域（RoI）进行池化操作，对于输入特征图 ，假设其中一块宽高分别为 
和 
、左上角位置为 的区域为 RoI ，将这块区域平均划分为 k * k 个子区域（bin），每个区域只输出一个值，即输出特征图 的大小为 k*k 。 对于 中的每个点 
，
，其值 
为：
其中 
为每个子区域（bin）中的像素点总数，式（5）是对 RoI 中的一个 bin 做了求均值的操作（把 bin 中的像素取平均值作为输出）。
2、Deformable RoI pooling：类似于上面的 Deformable Convolution ，我们也要去学习一个关于采样点位置的偏移量（offset）
，所以 Deformable RoI pooling 的计算式如下：
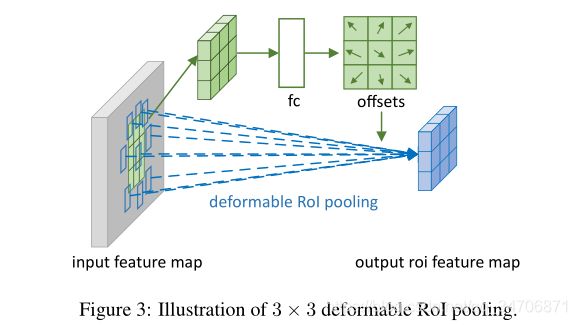
其对应的网络结构如下（Fig 3）：上面那条支路首先对输入特征图（input feature map）进行 RoI Pool 生成一个新的特征图，对新特征图进行一个全连接层（fc）的操作，生成了归一化的偏置（offsets）
， 将 和 RoI 的宽高做 element-wise product （元素层面上的乘积）得到所需的 ：
其中，
为一个预先定义好的标量。
三、Deformable Position-Sensitive (PS) RoI Pooling：可变形的、位置敏感的感兴趣区域池化
Position-Sensitive (PS) RoI Pooling 是一种全卷积的结构，引入了位置信息。Deformable PS RoI Pooling 结构如下：
和前面的Fig 2、Fig 3一样，这幅图上面部分的支路是 offsets 的生成，下面是常规的 PS RoI pooling，上下支路合起来就是 deformable PS RoI pooling 。先看下面的 PS RoI pooling，对于传进来的特征图（input feature map），进行 conv 操作，生成同空间分辨率的、通道数（channel）为 
的 score maps，其中 C 是我们要分类的类别数( +1 代表背景)，
是输出特征图的大小。若无 offsets ，我们要取的 bins 的空间位置在 scores maps 中的虚线部分，加入 offsets 后，要取的 bins 的空间位置偏移到了蓝色的 9 个框。需要注意的是，我们取这 9 个 bins 时，取的是在不同的 channel 维度上的 bin （每个 bin 的通道数为 
，即对应一种颜色的厚度），由上图可以看出 score maps 中在 channel 维度上有 （
时，即 9 ）种颜色， 与 output roi score map 中的颜色一一对应。 offsets fields 部分是通过卷积层生成的，channel 数为 
，这是因为总共有 个bins，每个bins 的 channel 数为 
，一个 offset 需要用两个数表示（二维空间）。
V2：
在 V2 的版本里，作者在 V1 的 Deformable Convolution 和 Deformable RoI Pooling 的基础上，加了一个控制输入强度的标量，
1、Deformable Convolution 表达式如下：
与上面 V1 中的（2）式相比，就多了一个可学习的标量 ![\Delta m_{k}\in [0,1]](http://img.e-com-net.com/image/info8/742e49012df74a0bb0731b0459400bb1.gif){kind=small}
，网络结构也与 V1 中的类似，只不过 其中 offset field 的通道数（channel）为 3K（V1 中是 2K ）， 前面 2K 对应可学习偏置 
，后面的 1K 对应强度控制 
。
2、Deformable RoI Pooling 的表达式如下：
也是多了一个 ，网络结构与上面的 Fig 3 类似，其支路具体为：input feature maps -> RoIpooling -> 1024D fc -> 1024D fc -> fc -> 3K channels ，同样前 2K channels 用于偏置 ，后面 1K channels 用于 。