【手把手带你学会KMP算法】

相信大家在遇到字符串匹配问题时，无论是听老师上课讲还是在网上查询资料时几乎都会用到KMP算法，本篇博客借鉴于大博哥对于KMP算法的分析以及自身对于KMP算法的看法，相信认真看完了后会对你有一些帮助。

 

目录

 1 BF 算法

2 KMP 算法

3 KMP算法的优化

---

---

 1 BF 算法

了解KMP算法之前，我们先来回忆一下BF算法(暴力求解），基本思想就是主串中元素与子串中元素一一比较，匹配失败就让子串返回到0下标，主串回溯到开始匹配的下一位。

假设主串的长度位M  子串的长度为N  BF算法的时间复杂度为 O(M*N)

 

动图详解（此图借鉴于其他博主）：

 

 具体代码：

int BF(char* mainStr, char* subStr,int pos)
{
	assert(mainStr && subStr);
	if (!*subStr)
	{
		return 0;
	}
	if (!*mainStr)
	{
		return -1;
	}

	int lenMain = strlen(mainStr);
	int lenSub = strlen(subStr);

	int i = pos; //遍历主串
	int j = 0; //遍历子串

	while (i < lenMain && j < lenSub)
	{
		if (mainStr[i] == subStr[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			j = 0;
		}
	}

	if (j == lenSub)
	{
		return i-j;
	}
	else
	{
		return -1;
	}
}

---

2 KMP 算法

KMP算法的诞生：KMP算法是三位大牛：Knuth、Morris和Pratt同时发现的，于是取了他们名字的首字母然后组合起来，就成了该算法的命名。（来自百度）

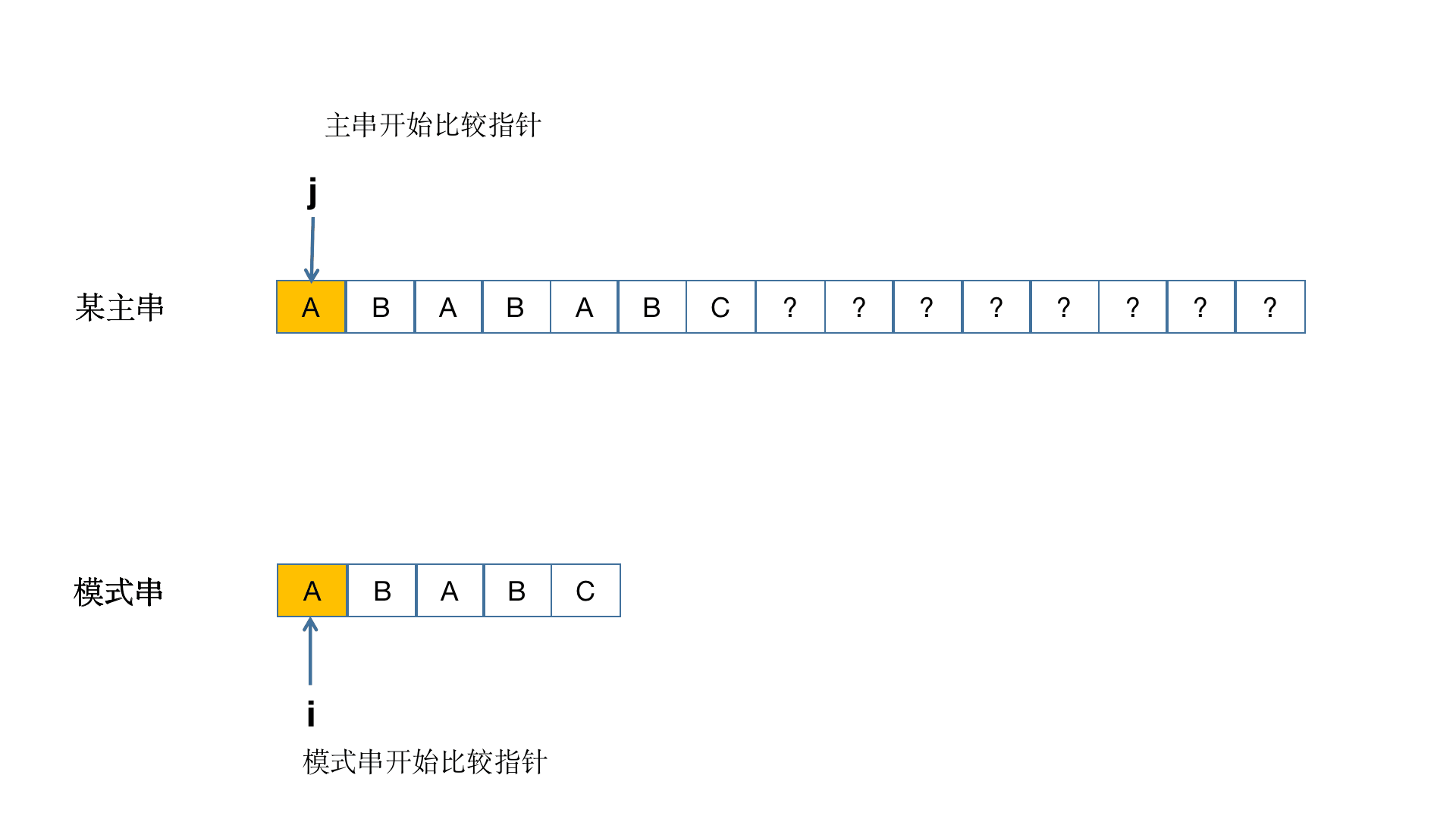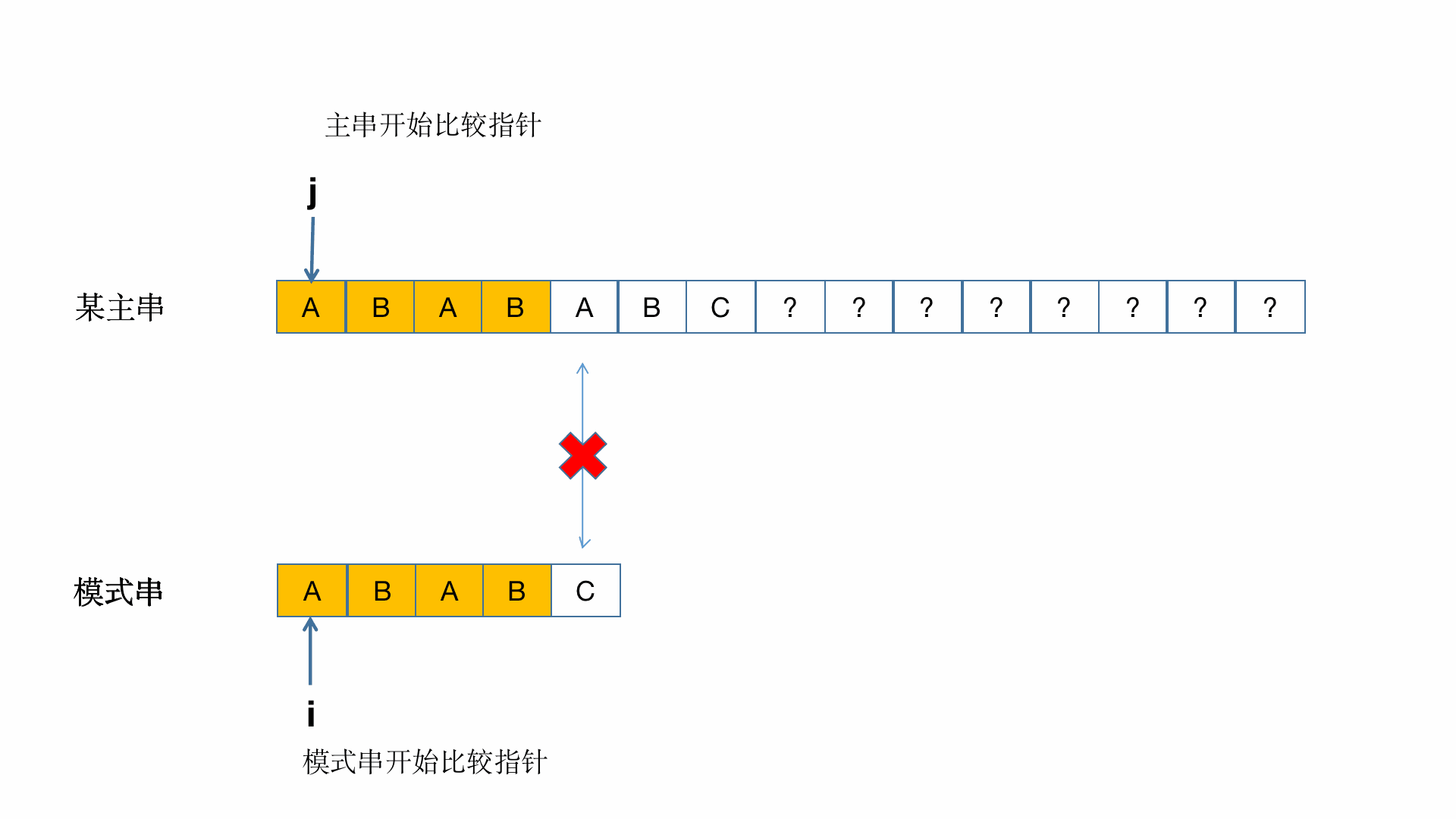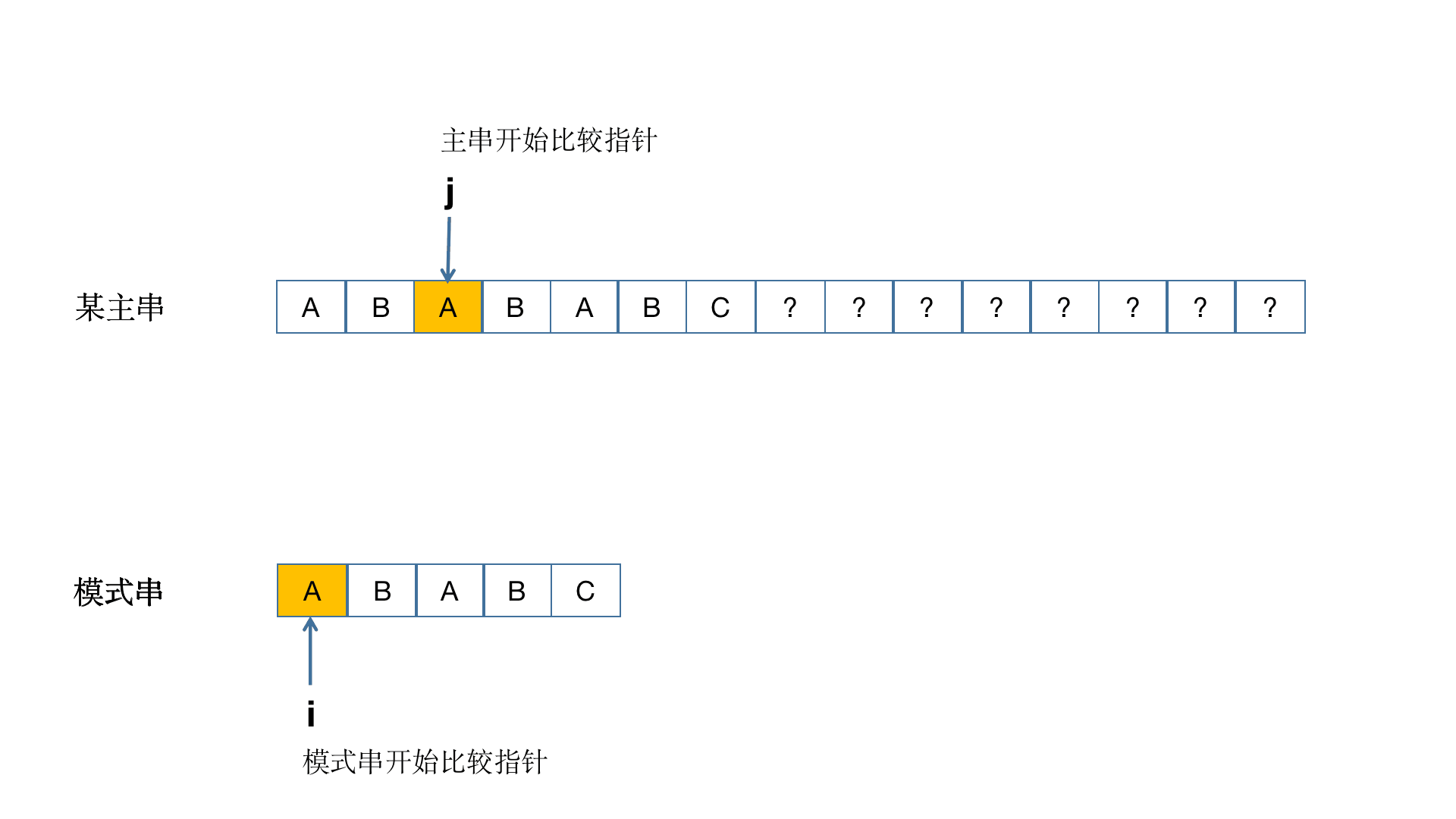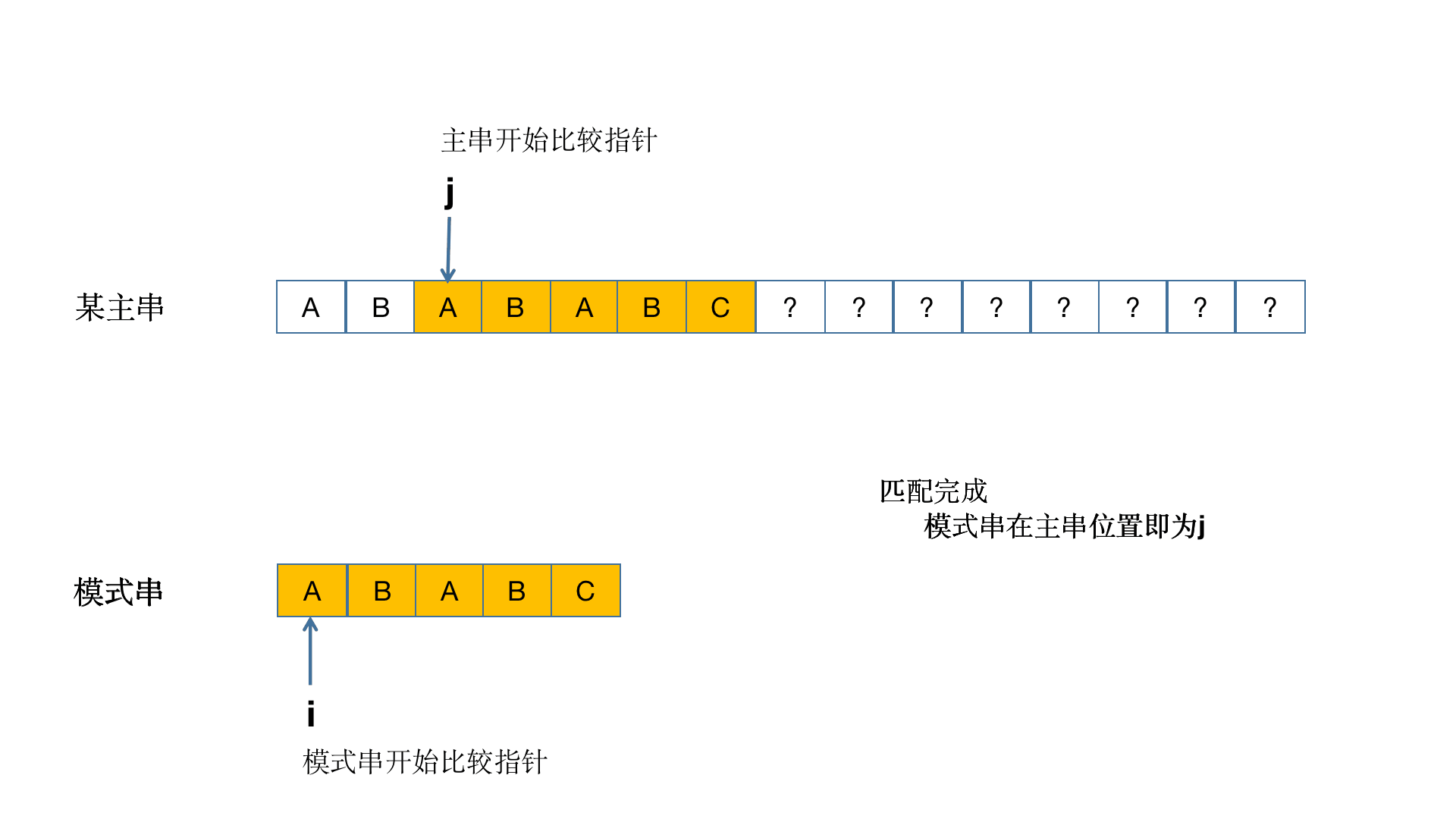
 kmp算法的主要思想是：在主串中查找子串时，利用主串和子串中已经匹配的部分，跳过一些无用的比较，使主串的标记指针不会回溯，子串的标记指针移动。其实主要是子串中如果有部分内容和主串中一致，我们需要研究这些已知的匹配内容，这相当于我们需要研究子串，发现子串中存在的规律。KMP算法的时间复杂度为 O(M+N)

 听起来是不是有点懵，没关系，我们来举个栗子：

主串：ababcabcdabcde

子串：abcd

由上述主串与子串数据可知目前在索引为2匹配失败，就算让主串回退到1也是没有必要的，因为主串中1位置字符b与子串0位置的a也不一样，所以我们的目的是：主串是不回退的，让子串回退到特定的位置。

那么子串应该回退到什么位置呢？ 再来举个栗子：

主串：abcababcabc

子串：abcabc

这里主串与子串在索引为5的位置不匹配，由于主串不回退，回退的是子串，通过肉眼观察我们发现子串回退到索引为2是比较合理的（我们要尽量在主串中找到和子串匹配的一部分串），由于主串中索引为5的字符a!=子串中索引为2的字符c,所以还要继续回退，直到回退到与字符a相等为止。那如果字符数量多了用肉眼观察肯定是不切合实际的，所以我们引出了next数组，用来保存子串中某个位置匹配失败后回退的位置。

KMP的精髓就是next数组，那么应该怎样来求next数组呢？假定next[j]=k;

求k的规则：

1. 找到匹配成功部分的两个相等的真子串（不包含本身）一个以下标0开始，另一个以j-1下标结束。
2. 总有next[0]=-1,next[1]=0。

有了上面的规则我们就可以来求next数组了：

栗子1：“ababcabcdabcde"

它对应的next数组为：[-1,0,0,1,2,0,1,2,0,0,1,2,0,0]

栗子2：”abcabcabcabcdabcde"

它对应的next数组为：[-1,0,0,0,1,2,3,4,5,6,7,8,9,0,1,2,3,0]

通过上面的栗子我们可以得出总结：找的时候可以找重复的，但是必须是以0下标开始，找的前一位下标结束；而且数组中元素增大只能一个一个的加，减小可以跳跃减小。

到这里我相信大家对求next数组应该没有什么问题了。但现在的问题是我们如何用公式来求next数组，总不能next数组让我们人为来算，这显然是不现实的。

我们假设已知:next[i]=k;

                                     k            i

给定一个字符串" a b c a b a b c a b c "

                           0 1 2 3 4 5 6 7 8 9 10

next数组:          [-1,0,0,0,1,2,1,2,3,4,5]

我们假设此时i==8

则我们可以知道：p[0]……p[k-1] == p[i-k]……p[i-1]

所以由:next[i]=k  <--->   p[0]……p[k-1] == p[i-k]……p[i-1]

如果现在 p[k]==p[i]  将其分别加在上式右边的两边得：

p[0]……p[k] == p[i-k]……p[i]

所以不难推出：next[i+1]=k+1；这也很好得解释了为什么增加只能一个一个的加。

那么问题又来了，如果p[k] != p[i]呢?

假设索引为8的元素由a改为b,那么k就要回退到next[k]的位置，也就是k=0，但还是不满足p[k]==p[i],就继续回退k=-1,此时已经找不到了，就直接将0给予给下一位，也就是：

next[i+1]=0；

 

 好了，next数组的求解概念已经掌握，现在我们如何用代码来将其表示出来呢？

代码的具体实现：

int KMP(char* mainStr, char* subStr, int pos)
{
	assert(mainStr && subStr);
	if (!*subStr)
	{
		return 0;
	}
	if (!*mainStr)
	{
		return -1;
	}

	int lenMain = strlen(mainStr);
	int lenSub = strlen(subStr);
	//动态申请next数组
	int* next = (int*)malloc(sizeof(int) * lenSub);
	if (NULL == next)
	{
		exit(-1);
	}
	GetNext(next,subStr);

	int i = pos; //遍历主串
	int j = 0; //遍历子串

	while (i < lenMain && j < lenSub)
	{
		if (mainStr[i] == subStr[j] || -1==j)
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];
		}
	}

	if (j == lenSub)
	{
		free(next);
		return i - j;
	}
	else
	{
		free(next);
		return -1;
	}

}

这里面有一个容易出错的点，当j==-1时也不要忘记了处理，当j==-1时说明回到了索引为0的位置，并且还没有找到与其匹配的项，就让j从索引为0开始与i一一比对。

得到next数组的具体代码：

void GetNext(int* next, int* subStr)
{
	assert(next && subStr);
	int lenSub = strlen(subStr);
	next[0] = -1;
	next[1] = 0;
	int i = 2;
	int k = 0;

	while (i < lenSub)
	{
		if ((-1 == k) || subStr[i - 1] == subStr[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = next[k];
		}
	}
}

由于这里的next[i]是未知的，而next[i-1]才是已知的，所以上面才是subStr[i - 1] == subStr[k]

next[i] = k + 1; 同理当k==-1时说明到索引为0都还没有匹配的项就把其置为0.

 

---

3 KMP算法的优化

假定给一个这样的字符串： " a a a a a a a a a a g "

它的next数组为：               [-1,0,1,2,3,4,5,6,7,8,9]      

 假设在索引为9的位置匹配失败，则j会不断回退直到j==-1,这样效率就比较低了，有什么办法能够一步到位回退呢？

我们不妨优化一下next数组：为了区别，不妨将将优化后的数组取名为nextval

nextval数组的规则如下：

1 如果回退到的位置和当前字符一样，就写回退那个位置的nextval值；

2 如果回退到的位置和当前字符不一样，就写当前原来的nextval值;

 举个栗子：给" a  b  c  a  a  b  b  c  a  b  c  a  a  b  d  a  b "

next:               [-1, 0, 0, 0, 1, 1, 2, 0, 0, 1, 2, 3, 4, 5, 6, 0,1]

nextval:          [-1, 0, 0,-1, 1, 0, 2, 0,-1, 0, 0,-1, 1, 0, 6,-1,0]

具体代码：

void GetNextval(int* nextval, int* subStr)
{
	assert(nextval && subStr);
	int lenSub = strlen(subStr);
	nextval[0] = -1;
	nextval[1] = 0;
	int i = 2;
	int k = 0;

	while (i < lenSub)
	{
		if ((-1 == k) || subStr[i - 1] == subStr[k])
		{
			nextval[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = nextval[k];
		}
	}
	i = 2;
	while (i < lenSub)
	{
		if (subStr[i] == subStr[nextval[i]])
		{
			nextval[i] = nextval[nextval[i]];
		}
		i++;
	}
}

---

好了，KMP算法就到这里了，如果有什么不对的地方欢迎各位佬在评论区指正。