数学建模——主成分分析及spss软件操作

主成分分析的基本原理：

一：什么是主成分分析？

        主成分分析是分析多个变量之间相关性的一种多元统计方法,研究如何通过少数几个主成分来解释多个变量之间的内部结构，即从原始变量中导出几个主分量，使他们尽可能多的保留原始变量的信息，且彼此间互不相关；

主成分分析的目的：数据的压缩+数据的解释

常被用来寻找判断事物或现象的综合指标，并对综合指标所包含的信息进行适当的解释

---

主成分分析的基本思想（以两个变量为例）：

1：对这两个变量所携带的信息进行浓缩处理

2：假定只有两个变量x1,x2,由散点图可见两个变量存在相关关系（例如这些点都近似存在于y=x这条直线上，x1=x2,这意味着两个变量提供的信息有重叠，如果不加处理，会消耗大量的时间精力处理数据。

3：如果把两个变量用一个变量来表示，同时这一个新的变量又尽可能包含原来的两个变量的信息，这就是降维的过程。

根据初始坐标轴x1x2，可看出所有数据点均可近似的看成存在于y=x的曲线上，现在将坐标轴旋转用于产生新的变量,变换后的坐标轴为y1,y2,此时变量y1,y2间看不到明显的函数关系,同时发现变量y1分布宽度更长，跨度比较大，说明变量y1包含了更大的信息量，且y1数据间变化更大，波动更大，进而方差更大，同时y2分布更窄，即变量y2所携带的信息量更小,对建模的结果的影响微乎其微,例如：通过一个班的考试成绩评估一个学生综合成绩的好坏，语文成绩相差很大且分布在各个阶段，每个人之间的成绩差异很大，重分的很少，而数学成绩全部分布在135左右，且相差不大，重分的人很多，那么你要评价一个学生综合成绩的好坏，不是只需要通过语文成绩的数据就可以分析了吗？，所以对于此例，我仅仅用y1的长轴就可以替换y2)

---

y1与x1,x2的关系

y1=a1x1+a2x2（保留数据）

y2=a3x1+a4x2（删除数据）

此时就将原来的x1,x2两个变量替换为y1,实现数据降维

所以主成分分析最关键的是找到旋转坐标轴的参数a1,a2，实现y和x1,x2逻辑关系

---

基本思想

主成分分析就是设法将原来众多具有一定相关性的变量（如p个变量),重新组合成一组新的相互无关的综合变量来代替原变量

通常数学上的处理就是将原来p个变量作线性组合作为新的综合变量

如果将选取的第一个线性组合即第一个综合变量记为F1，自然希望F1尽可能多的反映原来变量的值，如何反映？

最经典的方法就是使用方差来表达，即van(F1)越大，表示F1包含的信息越多，在所有的线性组合中方差最大的称为第一主成分

如果第一主成分不足以代表原来p个变量的信息，在考虑选取F2即第二个线性组合，F2称为第二主成分，那么F1F2间有何关系呢？

为了有效地反映原来的信息，F1已有的信息不要再出现在F2中，即Y1Y2协方差为0，即cov（Y1,Y2)=0，因此这些主成分之间是互不相关的，而且方差依次递减，以此类推可能会得到多个主成分，那么什么时候结束呢？

各主成分的累计方差贡献率>80%或特征根>1

---

数学模型

 要从原来的所有变量得到新的综合变量，一种较为简单的方法是做线性变换，使新的综合变量为原变量的线性组合

---

 数学模型的条件

对于任意常数c,有

        var(cF1)=var(F1)

为了使方差var(F1)可比较，要求线性组合的系数满足规范化体条件

即，线性组合中各变量的前置系数平方和为1

要求原始变量之间存在一定的相关性（相关系数分析：pearson,spearman见我空间）

要求各个综合变量间互不相关，即协方差为0

为了消除变量量纲不同对方差的影响，通常对数据进行标准化处理，变量之间的协方差即为相关系数

---

能否做主成分分析的两大检验

1：KMO检验结果>0.5

2：Bartlett's检验<0.05

满足上述条件一个即可

---

 计算过程推导公式需要良好的线性代数基础，我学的不好，在这里不做描述，数学建模会用matlab编程即可，使用spss也不需要掌握此过程,说白了就是laozi不会讲，你也不愿意听，数学建模也用不到。

---

 如果前k个主成分累计贡献率达到85%，则表明前k个主成分基本包含了全部测量指标的基本信息，从而达到了变量降维的目的。

注意：为了消除数据量纲不统一，通常将原始数据进行标准化处理！！！

这里给出一种处理数据的方法——归一化

Min-max 标准化

    新数据=（原数据-极小值）/（极大值-极小值）

    标准化以后，X中元素的取值范围是[0,1]。

　　
　　X = (X-Xmin))./(Xmax-Xmin);

代码部分：

1. [Y,PS] = mapminmax(X,YMIN,YMAX)
2. [Y,PS] = mapminmax(X,FP)
3. Y = mapminmax('apply',X,PS)
4. X = mapminmax('reverse',Y,PS)  %反归一化

对于1和2的调用形式来说，X是预处理的数据，Ymin和Ymax是期望的每一行的最小值与最大值，FP是一个结构体成员主要是FP.ymin, FP.ymax.这个结构体就可以代替Ymin和Ymax,1和2的处理效果一样，只不过参数的带入形式不同。不设置YMIN 和YMAX，归一化范围为0~1。
示例：

x=[2,3,4,5,6;7,8,9,10,11];
[Y,PS] = mapminmax(x,0,1);
fp.ymin=0;
fp.ymax=1;
[Y,PS] = mapminmax(x,fp);

结果：

0	0.250000000000000	0.500000000000000	0.750000000000000	1
0	0.250000000000000	0.500000000000000	0.750000000000000	1

以上是数学建模主成分分析理论准备，听不懂没事儿，下面案例

---

主成分分析的步骤

1：对原来的p个指标进行标准化，以消除变量在水平和量纲上的影响

2：根据标准化后的矩阵求出相关系数矩阵

3:求出协方差矩阵的特征根和特征向量

4：确定主成分，并对各主成分所包含的信息予以适当解释

---

---

---

案例

（spss中无法做主成分分析，这里我们采用的是因子分析！，并不影响结果）

根据我国31个省市自治区2006年的6项主要经济指标数据，进行主成分分析，找出主成分并进行适当解释

	A	B	C	D	E	F	G
1	地区	人均GDP （元）	财政收入 （万元）	固定资产投资 （亿元)	年末总人口 （万人）	居民消费水平 （元/人）	社会消费品零售总额 （亿元）
2	北京	50467	11171514	3296.4	1581	16770	3275.2
3	天津	41163	4170479	1820.5	1075	10564	1356.6
4	河北	16962	6205340	5470.2	6898	4945	3397.4
5	山西	14123	5833752	2255.7	3375	4843	1613.4
6	内蒙古	20053	3433774	3363.2	2397	5800	1595.3
7	辽宁	21788	8176718	5689.6	4271	6929	3434.6

题目分析：自变量过多,是否可以用更少的指标代替这6个变量，即数据降维，利用主成分实现替代

在spss中导入数据开始操作

 1:数据处理——量纲一致化操作（千万别忘！！！）

点击上方菜单栏——分析——描述统计——描述

 将变量导入，勾选“将标准化变量另存为变量”

 结果

 数据标准化结果

 接下来进行主成分分析，点击菜单栏“分析”——“降维”——“因子”

 将已经量纲一致化的数据导入右侧变量，点击右侧“描述”，在窗口中勾选“初始解”以及“KMO和巴特利特球型度检验”

 紧接着点击“提取”，在弹出的对话框中勾选“协方差矩阵”，剩下的参数默认不动

 接下来点击旋转，勾选“无”

 接下来点击得分，勾选“保存为变量”，勾选“显示因子得分系数矩阵”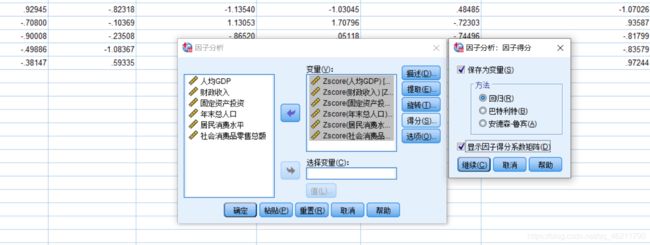

 点击确定输出结果

 由图可得，第一个特征值为3.042，第二个特征值为2.596，前两个主成分的累计贡献率之和为93.967%，超过85%，那么就选择这两个变量1，2为主成分

下面让我们来直观的分析我们所选取的主成分1，2和6个变量之间的成分矩阵（关联程度）

可以看出主成分1对于：人均GDP-0.877（负相关），固定资产投资-0.735（负相关)，年末总人口0.927，居民消费水平-0.836几个变量系数较大，所以主成分1可以很好的代表这四个变量，同理，主成分2替代了：财政收入以及社会消费品零售总额两个因子，可能有人会问了，凭啥我系数越大越能代表你呢？其实就是一个关联度相关性的问题，比如你开家长会，是不是你爸爸妈妈最可以代表你呢，因为爸爸妈妈和你的关联度最高啊，其次是哥哥姐姐啥的，对不？

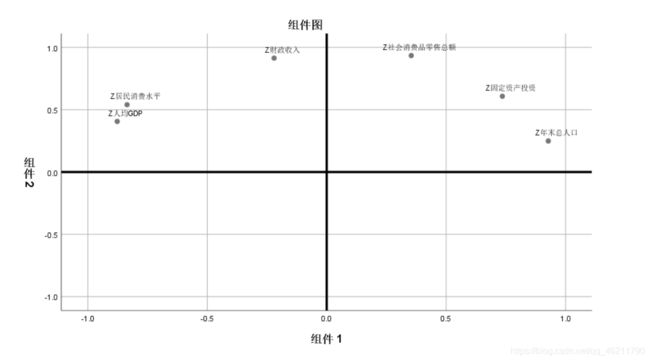
建模中可以通过展示载荷图将其更立体的展现出来，同时充实你的论文内容

那么如何输出载荷图？操作如下

顶部选择“分析”——“降维”——“因子”——旋转——勾选载荷图

 输出载荷图如下

 也可看出，横坐标为主成分1，纵坐标为主成分2，例如人均GDP,横坐标为-0.877，纵坐标为+0.406，其余变量同理。

或者可以尝试一下碎石图：

 输出图像

 规定：在比较大的斜率拐点处，发生明显的斜率变化，拐点之前可以作为主成分

---

这里我们再把成分矩阵摆在这里

一通猛如虎的分析之后，你还记得主成分分析的关键步骤吗，或者我们之前的操作是为了什么呢？

文章的开头说过，主成分分析最关键的是找到旋转坐标轴的参数a1,a2，实现y和x1,x2逻辑关系，现在的系数我们已经得到了吗？确实是得到了一些，比如成分矩阵里的-0、877，-0.220不正是第一第二主成分的前置系数吗？那接下来我们能直接写出y1=a1x1+a2x2的表达式吗?

答案肯定是不可以的，因为spss里没有专门针对主成分分析的操作，我们刚刚做的是因子分析，我们得到的是因子分析的系数矩阵，所以要进行变换，其中复杂的推导过程就不说了，因为我不会你不听数模用不到，假设因子分析法产生的一个前置系数为,我们要的是主成分分析法中各主成分的前置系数，计算公式为 uij=aij/(为贡献率),目前，我们已经得出因子分析法的成分矩阵，只需要除以根号下lamda即可得到真正的主成分分析法的前置系数，实在不理解为啥直接记住这步操作即可，

具体的spss操作如下，在原有的成分矩阵基础上点击——编辑内容——在查看器中

 选中数据

粘贴到表格中进行变换，更改变量名为V1,V2

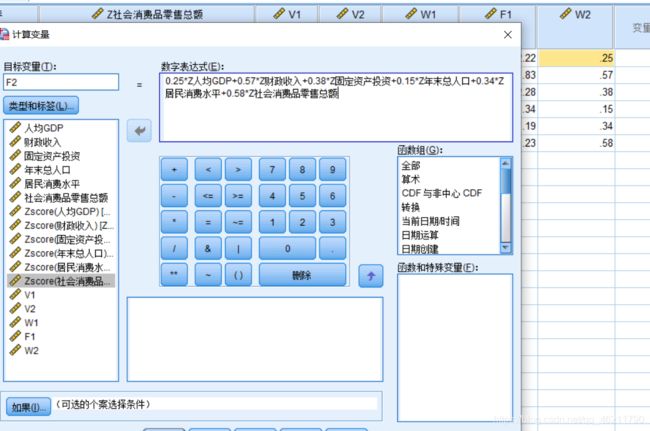
上方菜单栏点击——转换——计算

 

 计算真实的主成分分析前置系数（3.042是因子分析法得出的成分矩阵里的系数）

 计算结果W1，W1为第一主成分F1的前置系数

写出F1结果表达式

F1计算结果

由此，我们将原先的6个指标被我的一个指标F1代替，起到了降维的作用。

 

 F2计算方法同上，再次演示一遍

先计算前置系数W2，W2为第二主成分F2的前置系数

写出F2结果表达式

 

 

最终结果

至此，原先的六个变量变成了F1,F2两个变量，降维成功，主成分分析结束。（上图W2出现的数据乱码是截图时候产生的bug）

2021/7/24  0：56  留校中 后续会继续推出数学建模各种模型及代码，初次写博客，写的不好多多见谅，下一次更新一维二维插值算法+拟合算法（matlab编程）