入选2022年BookAuthority 的最佳量子计算新书:《与量子比特共舞》
说到计算机,大多数人想到的都是笔记本电脑,也有人可能会想到更大型的机器,比如支撑网络的服务器、互联网和云等。环顾四周,你也许还能在其他地方看见计算机。举个例子,现在的汽车装有大约20~100台计算机,这些计算机控制着汽车的运动和制动系统、监控着汽车空调和车载娱乐系统等。
智能手机也是计算机,很多人每天在智能手机上花的时间比在其他许多东西上花的都多。现代手机内部使用了64位处理器,但这里先不谈“64位处理器”是什么意思。运行所有应用程序所需的内存空间约为3 GB,也就是3吉字节。“吉”是什么,“字节”又是什么?
所有这些计算机都是经典计算机(classical computer),其最初的设计思路可以追溯到20世纪40年代。用更科学的说法,我们说这些计算机具有冯·诺依曼架构(von Neumann architecture),其得名于数学家兼物理学家约翰·冯·诺依曼(John von Neumann)。
当然,现在早已不再是20世纪40年代,但直到今天,我们日常生活中很多地方使用的计算机都仍旧是这种机器的现代版本。计算机中负责“思考”的组件是处理器。近年来,处理器的运行速度越来越快,计算机的内存空间也越来越大,这让我们可以运行更多、更大的应用程序,这些程序可以完成相当复杂的任务。图形处理器的发展为我们带来了越来越好的游戏体验。过去20年来,存储器的规模迎来爆发式增长,让我们可以将越来越多的应用、照片和视频存储在我们日常携带的设备中。说到经典计算机及其发展方式,其趋势总结起来就是在追求“越多越好”。
对于支撑全世界的企业运营和互联网应用的计算机服务器,也可以得出类似的结论。你是否在云中存储过自己的照片?这个云究竟在哪里?你在云中保存了多少照片?成本如何?你能以多快的速度从那个“说不清、道不明”的地方存取你的照片和其他数据?
着实惊人,这都是计算机的力量。看起来每一代计算机都会变得越来越快,它们能为我们做的事情也将越来越多。在为我们提供娱乐方式、方便我们与朋友和家人的联系,以及解决其他重要问题方面,这些或大或小的机器似乎还将继续变强,没有尽头。
但……事实并非如此。
尽管还会继续出现一些进步,但始于20世纪60年代中期的“每两年处理器能力倍增”的趋势将难以为继。这种倍增趋势被称为摩尔定律(Moore’s Law),其大致意思是:“每两年,处理器的速度会翻倍,尺寸会减半,能耗也会减半。”
这里的“翻倍”和“减半”都是近似的,但物理学家和工程师在这几十年中确实取得了非凡的进步,也因此,现在你的腕表几乎可以装下比最初需要占满一个房间的计算机更强大的计算机。
关键的问题在于处理器尺寸会减半的部分。我们无法无限地缩减晶体管和电路的尺寸。当我们将其尺寸缩减到接近原子大小时,电子器件将变得非常拥挤,以至于当我们想让处理器的某部分执行某项任务时,其相邻的部分也会受到影响。
另外还存在一个更深层、更涉及基础本质的问题:我们多年前创造了一种架构并对其进行了极大的改进,就一定意味着使用这种架构的计算机最终可以成功解决每种类型的问题吗?换句话说,我们凭什么认为我们现在拥有的各种计算机能够解决每个可能出现的问题。如果我们一直坚持使用同一种计算机技术,“越多越好”的趋势是否将后继无力?我们的计算方式是否存在错误或局限,让我们无法取得我们所需或想要的进步?
对于最后一个问题,不管你思考的是这个问题的哪个方面,都可以合理地认为其答案介于“可能是”或“确实是”之间。
真是让人沮丧的答案。好吧,其实只有当我们想不出一种或多种有望突破这些局限的新型计算机时,这样的答案才让人沮丧。
而这就是《与量子比特共舞》要谈的东西。量子计算的思想至少可以追溯到20世纪80年代早期,是一种基于量子力学原理而提出的全新类型的计算机架构。而量子力学的思想可以追溯到约一个世纪前,尤其是20世纪20年代——那时候物理学家开始注意到实验结果与理论预测不符的现象。
但是,《与量子比特共舞》关注的不是量子力学。自2016年以来,已有数万用户能通过云服务使用量子计算硬件了。这种云被称为“量子云服务”。人们开始为新型的量子计算机编写程序,不过为量子计算机编程的方法与为经典计算机编程的方法完全不同。
为什么量子计算吸引了如此之多的人?我确信一部分原因是好奇心。来看看科幻领域吧!“量子”这个词在科幻电影中出现的次数实在太多了,以至于观众也很好奇这个词的实质是什么。
一旦我们度过了觉得量子计算新颖、有趣的阶段,我们就会问“好吧,这究竟有什么用呢?”,以及“这将在什么时候以怎样的方式改变我们的生活?”。我将介绍专家认为的未来几年和几十年里最可能实现的用例。
是时候了解量子计算了。是时候停用经典的思维方式,开始量子地(quantumly)思考了(尽管我相信,在英语中,quantumly并不是个真实存在的词)!
与量子比特共舞
https://item.jd.com/13349281.htmlitem.jd.com/13349281.html
本书介绍量子计算的理论基础、基本原理和工作机制,帮助读者了解量子计算的基础和概况。全书共12章,首先介绍为什么要使用量子计算,然后分基础知识和量子计算两个部分,介绍量子计算所依赖的经典计算的相关知识,以及量子计算的工作机制,并展望量子计算的发展前景。
本书适合对量子计算感兴趣,并且想要学习和了解与量子计算相关的物理学、计算机科学和工程开发等知识的读者。
量子计算是下一个颠覆性的技术。本书旨在带领读者探究量子计算的工作原理,并深入解释背后的数学基础。同时,本书清晰地介绍了构建量子计算机的工程思想、基本的电路和算法,并对量子计算可能应用的几大行业以及未来的发展方向做出了展望。
本书特色:
从基础数学到量子计算的基本原理,步步为营,入门量子计算
很多示例来自IBM Q量子计算系统
专门设计了思考题,按章节编号,帮助读者消化吸收
本书入选Book Authority 2022年值得阅读的14本量子计算新书之一。(参见https://bookauthority.org/books/new-quantum-computing-books?t=g458j5&s=award&book=1838827366)
本书作者入选量子科技媒体Quantum Zeitgeist评选的“推动量子技术革命的20位最具影响力的人物”。(来源:光子盒)
本书得到了剑桥量子计算首席执行官Ilyas Khan和IBM Quantum开发倡导者James L. Weaver的大力推荐。
要阅读本书,读者不必是一位物理学家,也无须事先了解量子力学。
样章试读
第1章 为什么要使用量子计算?
自然并不是经典模式的,可恶。如果你想模拟自然,你最好使用量子力学来做。——理查德•费曼(Richard Feynman)
1965年的诺贝尔物理学奖获得者理查德•费曼在其1982年的论文《用计算机模拟物理学》(“Simulating Physics with Computers”)中说到,他想“探讨存在精准模拟的可能性,即计算机的行为与自然的行为完全一致的可能性。”然后他又说了上面的话,声称自然界的设计方式并不能使自己通过经典的二进制计算机进行计算。
我们将从这一章开始探索量子计算与经典计算的不同之处。经典计算驱动着当今的智能手机、笔记本电脑、互联网服务器、大型机、高性能计算机,乃至汽车中的处理器。
我们将探讨一些用例——这些用例目前还无法在经典计算机上使用经典方法解决,但未来某天也许会被量子计算攻克。这是为了激励你了解本书探讨的量子计算的基础和细节。
对于这一主题,仅用一本书是无法详尽介绍的。而且随着创新的继续,我们会创造出越来越好的硬件和软件,我们的技术和潜在用例目标也在不断变动。本书的目标是让你做好准备,以便能更深入地探究量子计算的编程和应用。
1.1 神秘的量子比特
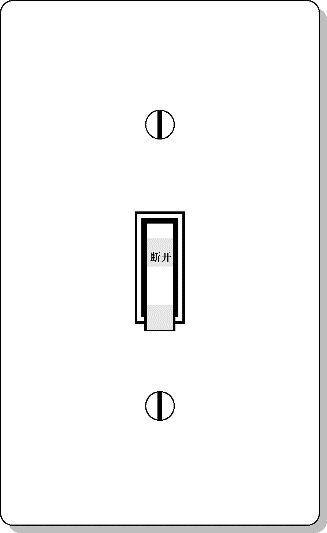
假设我正站在一个房间里,头顶上有一盏灯,旁边有一个可以开灯或关灯的开关(见图1-1)。这只是一个普通开关,所以我无法调节灯光亮度。要么全开,要么全关。我可以随意改变开关状态,但我也只能做这一件事。这个房间只有一扇门,没有窗户。当我在门外时,如果门关着,我看不见里面的任何光。
图1-1
我可以呆在房间里,也可以离开。取决于开关的位置,这盏灯要么亮起,要么熄灭。
现在,我要重新布线了。我将用这栋建筑里另一个地方的另一个开关替换原本的开关。现在我完全看不见灯,但同样地,这盏灯的亮灭状态完全由这个开关的两个位置决定。
如果我走向装有这盏灯的房间并打开门,我可以看到该灯是亮还是灭。我可以进出该房间任意次,这盏灯的状态依然由那个或开或关的开关所决定。这盏灯是“经典模式的”。
现在,让我们想象一组采用量子模式的灯和开关,我们分别称之为“量子灯”和“量子开关”。
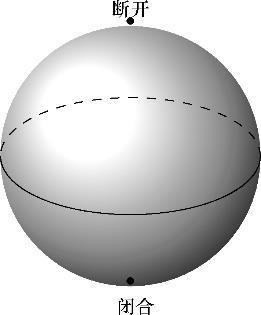
当我走进有这盏量子灯的房间时,和之前一样,它要么亮起,要么熄灭。这个量子开关和普通开关不一样,它的形状像一个球(见图1-2),其顶部(不妨称为北极)表示“断开”,底部(不妨称为南极)则表示“闭合”。而在这个球的中部,刻了一条线。
图1-2
当我在这栋建筑里有量子开关却看不见量子灯的地方时,有意思的情况出现了。
我将手指放在量子开关的球面上来控制这个开关。如果我将手指放在北极,则量子灯肯定熄灭;如果我将手指放在南极,则量子灯必然亮起。你可以走进房间查看,也总是能得到上述结果。
如果我把手指移到量子开关球面的其他任何地方,这个量子灯在你查看时可能处于熄灭或亮起状态。如果你不查看,则这个量子灯可能处于一种中间状态:它并非变暗了,也并非处于熄灭或亮起状态,它只是在被查看时以一定概率处于熄灭或亮起状态。这实在非同寻常!
在你打开门看见量子灯的瞬间,这种不确定性就会消除。灯要么亮起,要么熄灭。此外,如果此时我的手指正放在量子开关上,那么这根手指会被迫移动到南极或北极位置,其分别对应于所看见的量子灯的亮灭状态。
查看量子灯这一行为会迫使开关进入闭合或断开状态。我不必看到量子灯本身,只要我打开一点点门,能看见灯是否在发光就够了。
如果我在有量子灯的房间里放一个摄像机,然后在看视频的同时将我的手指放在量子开关上,则这个开关的行为模式将与普通开关完全一样。除了顶部和底部,我将无法触碰这个量子开关的其他任何地方。既然我构想了这个案例,那就假设存在某种阻碍我触碰极点外其他任何位置的力场吧!
如果你或我都没有以任何方式查看这个量子灯,那么我触碰这个量子开关时的情形又会有何不同?触碰其北半球或南半球是否会影响量子灯在我查看时的亮灭状态?
会的。触碰量子开关上更接近北极或南极的位置会分别使得量子灯熄灭或亮起的概率更高。如果我将手指放在极点之间的圆圈(赤道)上,则量子灯亮起或熄灭的概率刚好各为50%。
以上描述的系统被称为二态量子系统(two-state quantum system)。当量子灯未被查看时,它处于亮起和熄灭的叠加(superposition)状态。我们将在7.1节探索叠加。
尽管这可能看起来很奇怪,但有证据表明大自然就是这样运作的。电子具有一种被称为“自旋(spin)”的属性。在这一属性的基础上,电子就是一种二态量子系统。构成光的光子本身就是一种二态量子系统。我们将在11.3节介绍极化(polarization,也称“偏振”,偏光太阳镜中便用到了极化)时涉及这一主题。
对本书而言更重要的量子比特(quantum bit,常写为qubit,也称“量子位”)也是一种二态量子系统。量子比特是对经典计算中比特概念的扩展和补充,而比特要么为0,要么为1。量子比特是量子计算中的基本信息单位。
本书要讲的是通过操纵量子比特使目前仅使用经典计算无法攻克的问题得到解决的方法。对于某些问题,似乎仅使用0或1是十分难以解决的,而如果坚持使用0或1,所需的时间和内存都将多得不切实际。
使用量子比特时,我们将亮起或熄灭对应的术语1或0分别替换为
![]()
和
![]()
。我们也不再使用量子灯这一说法,从现在开始将其称为量子比特。
在图1-3中,你的手指在量子开关上的位置现在由两个角度表示:
![]()
和
![]()
。图1-3本身被称为布洛赫球面,这是量子比特的一种标准表示方法,我们将在7.5节介绍它。
图1-3
1.2 我没有犯困!
如果我们可以不用实验室里的试管或烧杯,而是在计算机中进行化学反应,会如何呢?如果进行一个新实验就像运行一个应用程序那么简单,只需几秒钟就能完成,又会如何呢?
要真正实现这一点,我们需要程序能完全保真地完成这项任务。计算机中建模的原子和分子的行为应该与试管中的原子和分子的行为完全一致。物理世界中发生的化学反应需要精准的计算来模拟。我们将需要完全忠实的模拟。
如果我们能大规模地做到这一点,也许就能算出我们需要的分子(这些分子可能是一种用于洗发水的新材料,甚至是一种用于汽车和飞机的新型合金);也许我们可以更高效地发现针对你的生理机能定制的药物;也许我们可以更好地理解蛋白质折叠的方式,并由此理解它们的功能,进而有可能创造出能为我们的身体带来积极转变的定制酶。
这看起来可以实现吗?虽然我们已经有能运行各种模拟程序的大型超级计算机了,但我们现在能以上述方式为分子建模吗?
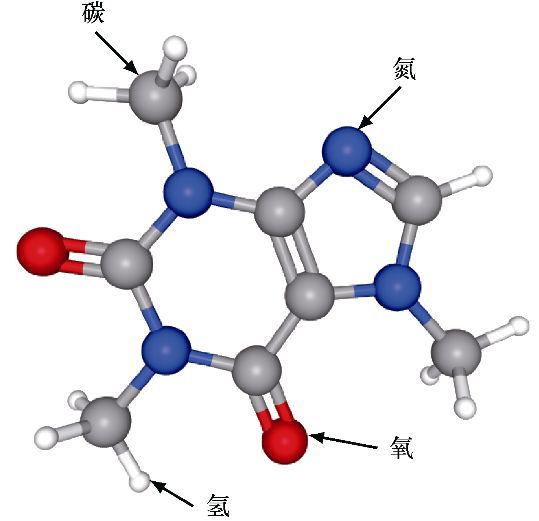
我们以1,3,7-三甲基黄嘌呤为例来谈谈吧(见图1-4),它的分子式为
![]()
。这种化学名称晦涩难懂的分子其实每天都被全世界数以百万计的人享用——它还有另一个名称:咖啡因。一杯8盎司①的咖啡约含95 mg咖啡因,也就是约
![]()
个分子,即:
295000000000000000000个分子
图1-4
① 盎司(ounce)既是重量单位又是容量单位。在此处表示液体盎司,1盎司约为29.57 mL,8盎司约为236.56 mL,后文的12盎司约为354.84 mL。——译者注
常见的12盎司可乐约含32 mg咖啡因,健怡可乐约含42 mg咖啡因,能量饮料通常约含77 mg咖啡因。[11]
问题1.2.1
你每天会喝下多少咖啡因分子?
分子数很多,因为我们是在数宇宙中物体的数量,而我们知道宇宙很大。举个例子,科学家估计单是地球,原子数量级就在
![]()
~
![]()
。
我们找个语境来看看这些数字:
![]()
,
![]()
,
![]()
,以此类推。1 GB等于109字节,1 TB等于
![]()
字节。
回到本节开始时提出的问题:我们可以在计算机中精准地为咖啡因建模吗?我们不是必须要为一杯咖啡中的大量咖啡因建模,但我们可以完全表征某一瞬间的单个分子吗?
咖啡因是一种小分子,其中包含了质子、中子和电子。特殊地,就算我们只描述决定分子结构的能量构型以及将分子聚合在一起的键,该分子的信息量也多得惊人。具体来说,所需的比特数,即0和1的数量,大约为
![]()
,即:
10000000000000000000000000000000000000000000000000
再看看之前的内容,这差不多相当于地球原子总数的1%~10%。
这还只是一个分子!尽管如此,大自然还是能以某种方式相当高效地处理这些信息。大自然能处理单个咖啡因分子,也能处理咖啡、茶和其他软饮中所有的咖啡因分子,还能处理构成你及周遭世界的每一个分子。
大自然是怎么做到的?我们不知道!当然,理论还是有的,它们处于物理学和哲学的交汇处,但我们并不需要完全理解也能将其利用起来。
按照传统的方式,我们没法使用足够的存储空间来容纳如此之多的信息。我们想要获得精准表征的梦想似乎就此破灭了。这正是本章开始时引述的理查德•费曼(见图1-5)所说的“自然并不是经典模式的”的含义。
图1-5 1959年,理查德•费曼在美国加州理工学院。照片属于公共领域
但是,当使用量子比特来执行计算时,160 个量子比特就能容纳
![]()
比特的信息。先说清楚,我不会介绍我们该如何将这些数据放入量子比特,我也不会谈如果我们要用这些信息来做一些有趣的事情,我们还需要多少量子比特。但是,量子比特确实带来了希望。
使用经典方法时,我们永远无法完整表征一个咖啡因分子。未来,当我们有了足够强大的量子计算系统,其中包含了足够多质量极高的量子比特时,也许我们就能在计算机中进行化学研究了。
了解更多
在量子化学这个科学领域中,量子计算机也许最终会被用于计算分子性质和蛋白质折叠构型等任务,但怎样能做到这一点却并不是三言两语就能说清的。尽管如此,前文的为咖啡因分子建模就是量子模拟(quantum simulation)的一个例子。
如果你想了解截至2019年在化学领域应用量子计算的历史和最佳方法,可以参考Cao等人的综述[2]。如果你想理解规模化地进行分子的量子模拟这个具体问题及其与高性能计算机的交织情况,可参考Kandala等人的文章[10]。
1.3 量子计算为什么不一样
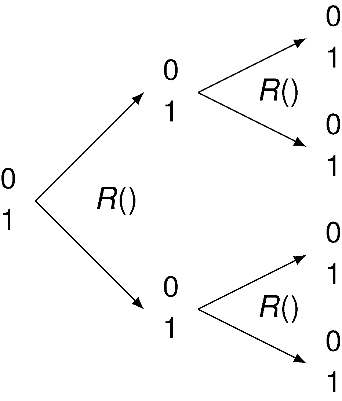
我可以在经典计算机上写一个模拟掷硬币的小应用程序。这个应用程序可以在我的手机或笔记本电脑上进行。
我们不使用正面或反面,而使用1和0。我将这个例程称为R,其初值为1或0,然后随机返回1或0。也就是说,它有50%的概率会返回1,50%的概率会返回0。不管R以怎样的方式做了什么,我们都不知道。当你看到“R”,要想到random(随机)。
这被称为公平抛掷(fair flip)。它没有经过加权,不会略微偏好其中某个结果。我们究竟能否在经典计算机上得到真正随机的结果则是另外一个问题。在这里,先假设我们的应用程序是公平的。
如果将R的初值设为 1,则可以预计其有50%的概率返回1,有50%的概率返回0;如果将R的初值设为0,结果也是一样的。我称这两个应用程序分别为R(1)和R(0)。
如果只看R(1)或R(0)的结果,没办法分辨R的初值究竟是1还是0。这就像是在神秘的掷硬币游戏中,无法仅凭硬币落地后的情况知道硬币是从正面还是反面朝上的情况开始抛掷的。我说掷硬币游戏“神秘”,是因为我能看到掷硬币的结果,但我对抛掷行为本身的机制或硬币的初始状态一无所知。
如果R(1)和R(0)都随机为1和0,那当执行R两次(图1-6)时又会发生什么?
图1-6
我将其写作R(R(1))和R(R(0))。答案还是一样的:均等分配的随机结果。不管我们执行R多少次,情况总是一样的:结果是随机的,我们不能反向推断出初始值。用5.3节中的术语来说:R是不可逆的。
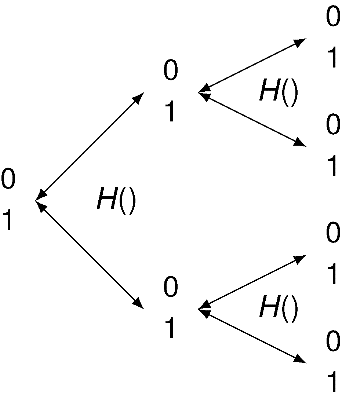
现在来看量子版本。我不再使用R,而使用H(图1-7),我们将在7.6节学到它。它也能以同等的概率返回0或1,但它还有两个有趣的性质。
图1-7
(1)它是可逆的。尽管无论是从1还是从0开始,它都会随机得到1或0,但我们总是能反过来查看初始时的值。
(2)它是其本身的逆运算或反运算。连续执行两次的结果就相当于什么也不做。
但是,这里有个陷阱。如果你想要逆转H的结果,那么你就不能查看H的结果。
如果我们将H的初值设为0或1,执行并查看结果,然后再次执行H,那么结果就与使用R的一样了。在量子设置中,如果你在错误的时间执行了观测,你就直接回到了严格经典的行为。
使用掷硬币的术语来总结一下:如果你抛掷的是一枚量子硬币,抛掷后不去查看它,然后再次抛掷,就会得到你开始时的正面或反面;如果你看了,得到的就是经典的随机结果。
问题1.3.1
请将该行为与1.1节的量子开关和量子灯的行为进行比较。
量子的另一个不同之处是处理同时值(simultaneous value)的方式。通常手机或笔记本电脑将字节(byte,记为B)作为内存或存储器的基本单位,因此我们有“兆字节”(megabyte,记为MB)这样的短语,其意思是一百万字节。
一个字节又可进一步分解为8个我们之前已经见过的比特。每个比特都可能是0或1。算一算,每个字节都能表示为有
![]()
种可能性的用8个0或1构成的数字,但它一次只能保留一个值。
8个量子比特则可以同时表示256个值。
这是通过叠加实现的,但也要用到纠缠(entanglement),这样我们才能将两个或多个量子比特的行为紧密地关联在一起。正因如此,对于我们在1.2节提到的咖啡因示例,如果使用量子表征,我们就能为工作内存大小带来指数级增长(实实在在的)。我们将在8.2节探索纠缠。