K-均值聚类算法
一. 机器学习中有两类的大问题
- 分类
分类是根据一些给定的已知类别标号的样本,训练某种学习机器,使它能够对未知类别的样本进行分类。 supervised learning(监督学习)
- 聚类
聚类指事先并不知道任何样本的类别标号,l类似于分类和回归中的目标变量事先并不存在,希望通过某种算法来把一组未知类别的样本划分成若干类别 unsupervised learning (无监督学习)
二. 最大区别
分类的目标类别 已知
聚类的目标类别 未知
与分类输入数据X预测变量Y不同,聚类是从X数据中我们能发现什么,而我们下面要讲解的K-均值聚类算法属于无监督学习
三. 优缺点
-
优点:容易实现。
-
缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢
-
适用数据类型:数据型数据
四. 原理
我特别喜欢这位博主对于这种算法生动的讲解
K-Means 聚类算法的大致意思就是“物以类聚,人以群分”:
1. 首先输入 k 的值,即我们指定希望通过聚类得到 k 个分组;
2. 从数据集中随机选取 k 个数据点作为初始大佬(质心);
3. 对集合中每一个小弟,计算与每一个大佬的距离,离哪个大佬距离近,就跟定哪个大佬。
4. 这时每一个大佬手下都聚集了一票小弟,这时候召开选举大会,每一群选出新的大佬(即通过算法选出新的质心)。
5. 如果新大佬和老大佬之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止。
6. 如果新大佬和老大佬距离变化很大,需要迭代3~5步骤。
那比较官方的解释呢就是
创建k个点作为起始质心,可以随机选择(位于数据边界内)
当任意一个点的簇分配结果发生改变时
对数据集中每一个点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
五.在了解原理后,我们将一步一步学习怎么构建K-均值聚类算法
- K-均值聚类算法De三个支持函数
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
"""
函数说明:
加载数据函数
"""
def loadDataSet(filename):
#初始化返回变量
dataMat = []
fr = open(filename)
for line in fr.readlines():
#数据集文件中每一行代表一个点的坐标,坐标与坐标之间采用制表符“\t"分隔,读取数据时要注意正确切割
curLine = line.strip().split('\t')
#python3和2的区别
#python2的map返回方式是list,python3返回的是iterators,需要加上list进行强制转换
fltLine = list(map(float,curLine))
#dataMat.append(xxx)填充数据
dataMat.append(fltLine)
return dataMat
"""
函数说明:
计算欧式距离
"""
def distEclud(vecA,vecB):
return sqrt(sum(power(vecA-vecB,2)))
"""
函数说明:
randCent 函数随机产生 k个质心 (质心必须在特征点边界内)
该函数为给定数据集构建一个包含k个随机质心的集合,随机质心必须要在整个数据集的边界之内,可以通过找到数据集每一维的最小和最大值来完成,然后生成0-1之间的随机数并通过取值范围和最小值,一边确保随机点在数据的边界之内。
"""
def randCent(dataSet, k):
#获取数据集中的坐标维度
#得到n=2
n = shape(dataSet)[1]
#初始化为一个(k,n)的矩阵保存随机生成的k个质心
centroids = mat(zeros((k,n)))
#遍历数据集的每一维度
for j in range(n):
#获取该列的最小值
minJ = min(dataSet[:,j])
#获取该列的最大值
maxJ = max(dataSet[:,j])
#得到该列数据的范围(最大值-最小值)
rangeJ = float(max(dataSet[:,j]) - minJ)
# k个质心向量的第j维数据值随机为位于(最小值,最大值)内的某一值
centroids[:,j] = minJ + rangeJ * random.rand(k,1)
return centroids
if __name__ == '__main__':
dataSet = loadDataSet('testSet.txt')
dataMat = mat(dataSet) # 将列表转为mat矩阵
print("第一维度min: %f max: %f " % (min(dataMat[:, 0]), max(dataMat[:, 0])))
print("第二维度min: %f max: %f " % (min(dataMat[:, 1]), max(dataMat[:, 1])))
print('看看randCent函数能否生成min和max之间的值')
range = randCent(dataMat, 2)
print(range)
print('测试计算距离公式')
print(distEclud(dataMat[0], dataMat[1]))
六. 接下来就可以实现完整的K-均值聚类算法
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
"""
函数说明:
加载数据函数
"""
def loadDataSet(filename):
#初始化返回变量
dataMat = []
fr = open(filename)
for line in fr.readlines():
#数据集文件中每一行代表一个点的坐标,坐标与坐标之间采用制表符“\t"分隔,读取数据时要注意正确切割
curLine = line.strip().split('\t')
#python3和2的区别
#python2的map返回方式是list,python3返回的是iterators,需要加上list进行强制转换
fltLine = list(map(float,curLine))
#dataMat.append(xxx)填充数据
dataMat.append(fltLine)
return dataMat
"""
函数说明:
计算欧式距离
"""
def distEclud(vecA,vecB):
return sqrt(sum(power(vecA-vecB,2)))
"""
函数说明:
为给定数据集构建一个包含k个随机质心的集合
随机质心必须要在整个数据集的边界之内,可以通过找到数据集每一维的最小和最大值来完成
创建k个点作为起始质心,可以随机选择(位于数据边界内)
当任意一个点的簇分配结果发生改变时
对数据集中每一个点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
"""
def randCent(dataSet, k):
#获取数据集中的坐标维度
#得到n=2
n = shape(dataSet)[1]
#初始化为一个(k,n)的矩阵保存随机生成的k个质心
centroids = mat(zeros((k,n)))
#遍历数据集的每一维度
for j in range(n):
#获取该列的最小值
minJ = min(dataSet[:,j])
#获取该列的最大值
maxJ = max(dataSet[:,j])
#得到该列数据的范围(最大值-最小值)
rangeJ = float(max(dataSet[:,j]) - minJ)
# k个质心向量的第j维数据值随机为位于(最小值,最大值)内的某一值
centroids[:,j] = minJ + rangeJ * random.rand(k,1)
return centroids
"""
函数说明:
k-means 聚类算法
该算法会创建k个质心,然后将每个点分配到最近的质心,再重新计算质心。
这个过程重复数次,直到数据点的簇分配结果不再改变位置。
"""
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
#返回行数
m = shape(dataSet)[0]
#创建一个与dataSet行数一样,但是有两列的m*2矩阵,用来保存簇分配结果
clusterAssment = mat(zeros((m, 2)))
#createCent=randCent,既然都使用randCent了,那就是创建随机k个质心
centroids = createCent(dataSet, k)
#聚类结果是否发生变化的布尔类型
clusterChanged = True
while clusterChanged:
#聚类结果是否发生变化置为false
clusterChanged = False
#遍历数据集每一个样本向量
#循环每一个数据点并分配到最近的质心中去
for i in range(m):
#初始化最小距离最正无穷
minDist = inf
#最小距离对应索引为-1
minIndex = -1
#依次循环k个质心
for j in range(k):
#计算某个数据点到质心的距离,欧式距离
distJI = distMeas(centroids[j,:],dataSet[i,:])
#如果距离比minDist(最小距离)还小
if distJI < minDist:
#更新minDist(最小距离)和最小质心的index(索引)
minDist = distJI
minIndex = j
#当前聚类结果中第i个样本的聚类结果发生变化:
if clusterAssment[i, 0] != minIndex:
#布尔类型置为true,继续聚类算法
clusterChanged = True
#更新簇分配结果为最小质心的 index(索引),minDist(最小距离)的平方
clusterAssment[i, :] = minIndex,minDist**2
#打印k-均值聚类的质心
print(centroids)
#遍历每一个质心
for cent in range(k):
#获取该簇中的所有点
#将数据集中所有属于当前质心类的样本通过条件过滤筛选出来
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A==cent)[0]]
#将质心修改为簇中所有点的平均值,mean 就是求平均值的
#计算这些数据的平均值(axis=0:求列的均值),作为该类质心向量
centroids[cent,:] = mean(ptsInClust, axis=0)
#返回k个聚类,聚类结果与误差
return centroids, clusterAssment
"""
函数说明:
绘制散点函数
"""
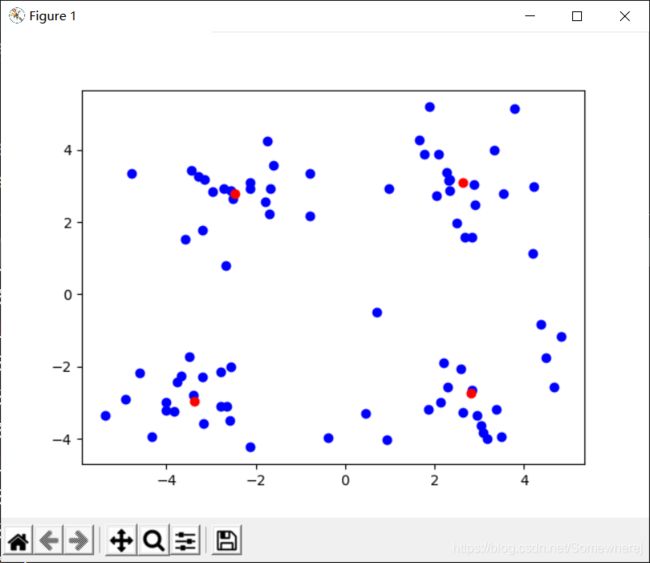
def paint(xArr,yArr,xArr1,yArr1):
fig = plt.figure()
ax = fig.add_subplot(111)
#散点(xArr,yArr)
ax.scatter(xArr,yArr,c='blue')
#质心(xArr1,yArr1)
ax.scatter(xArr1,yArr1,c='red')
plt.show()
if __name__ == '__main__':
dataMat = np.mat(loadDataSet('testSet.txt'))
myCentroids,clusterAssment = kMeans(dataMat, 4)
xArr = dataMat[:,0].flatten().A[0]
yArr = dataMat[:,1].flatten().A[0]
xArr1 = myCentroids[:,0].flatten().A[0]
yArr1 = myCentroids[:,1].flatten().A[0]
#进行数据的可视化
paint(xArr,yArr,xArr1,yArr1)
小总结
-
我们也可以很明显的感觉到,计算距离的函数时可选的,也就是说距离量度时可以变换的,你可以采用欧式距离,也可以采用余弦距离。
-
在算法中,采用计算质心-分配-重新计算质心的方式反复迭代(迭代使用while循环来实现),算法停止的条件是,当然数据集所有的点分配的距其最近的簇不在发生变化时,就停止分配,更新所有簇的质心后,返回二维矩阵clusterAssment。
- 一列记录k个类的质心(一般是向量的形式)组成的质心列表(簇索引值)
- 一列存储各个数据点到簇质心的距离(简称误差)
七. 使用后处理来提高聚类性能
其实通过上面的程序运行图,我们也可以看出,点的簇分配结果没有那么准确。因为K-means算法采取的是随机初始化k个簇的质心的方式, 聚类效果又可能陷入局部最优解的情况,局部最优解虽然效果不错,但不如全局最优解的聚类效果更好。因此后续会在算法结束后,我们应当采取相应的后处理。
方法
- 增加簇的个数,但是违背了聚类的目标(在保持簇数目不变的情况下提高簇的质量)
- 使用二分K-均值聚类算法,伪代码如下:
将所有数据点看成一个簇
当簇数目小于k时
对每一个簇
计算总误差
在给定的簇上面进行k-均值聚类(k=2)
计算将该簇一分为二后的总误差
选择使得误差最小的那个簇进行划分操作
实现代码如下
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
"""
函数说明:
加载数据函数
"""
def loadDataSet(filename):
#初始化返回变量
dataMat = []
fr = open(filename)
for line in fr.readlines():
#数据集文件中每一行代表一个点的坐标,坐标与坐标之间采用制表符“\t"分隔,读取数据时要注意正确切割
curLine = line.strip().split('\t')
#python3和2的区别
#python2的map返回方式是list,python3返回的是iterators,需要加上list进行强制转换
fltLine = list(map(float,curLine))
#dataMat.append(xxx)填充数据
dataMat.append(fltLine)
return dataMat
"""
函数说明:
计算欧式距离
"""
def distEclud(vecA,vecB):
return sqrt(sum(power(vecA-vecB,2)))
"""
函数说明:
为给定数据集构建一个包含k个随机质心的集合
随机质心必须要在整个数据集的边界之内,可以通过找到数据集每一维的最小和最大值来完成
创建k个点作为起始质心,可以随机选择(位于数据边界内)
当任意一个点的簇分配结果发生改变时
对数据集中每一个点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
"""
def randCent(dataSet, k):
#获取数据集中的坐标维度
#得到n=2
n = shape(dataSet)[1]
#初始化为一个(k,n)的矩阵保存随机生成的k个质心
centroids = mat(zeros((k,n)))
#遍历数据集的每一维度
for j in range(n):
#获取该列的最小值
minJ = min(dataSet[:,j])
#获取该列的最大值
maxJ = max(dataSet[:,j])
#得到该列数据的范围(最大值-最小值)
rangeJ = float(max(dataSet[:,j]) - minJ)
# k个质心向量的第j维数据值随机为位于(最小值,最大值)内的某一值
centroids[:,j] = minJ + rangeJ * random.rand(k,1)
return centroids
"""
函数说明:
k-means 聚类算法
该算法会创建k个质心,然后将每个点分配到最近的质心,再重新计算质心。
这个过程重复数次,直到数据点的簇分配结果不再改变位置。
"""
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
#返回行数
m = shape(dataSet)[0]
#创建一个与dataSet行数一样,但是有两列的m*2矩阵,用来保存簇分配结果
clusterAssment = mat(zeros((m, 2)))
#createCent=randCent,既然都使用randCent了,那就是创建随机k个质心
centroids = createCent(dataSet, k)
#聚类结果是否发生变化的布尔类型
clusterChanged = True
while clusterChanged:
#聚类结果是否发生变化置为false
clusterChanged = False
#遍历数据集每一个样本向量
#循环每一个数据点并分配到最近的质心中去
for i in range(m):
#初始化最小距离最正无穷
minDist = inf
#最小距离对应索引为-1
minIndex = -1
#依次循环k个质心
for j in range(k):
#计算某个数据点到质心的距离,欧式距离
distJI = distMeas(centroids[j,:],dataSet[i,:])
#如果距离比minDist(最小距离)还小
if distJI < minDist:
#更新minDist(最小距离)和最小质心的index(索引)
minDist = distJI
minIndex = j
#当前聚类结果中第i个样本的聚类结果发生变化:
if clusterAssment[i, 0] != minIndex:
#布尔类型置为true,继续聚类算法
clusterChanged = True
#更新簇分配结果为最小质心的 index(索引),minDist(最小距离)的平方
clusterAssment[i, :] = minIndex,minDist**2
#打印k-均值聚类的质心
print(centroids)
#遍历每一个质心
for cent in range(k):
#获取该簇中的所有点
#将数据集中所有属于当前质心类的样本通过条件过滤筛选出来
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A==cent)[0]]
#将质心修改为簇中所有点的平均值,mean 就是求平均值的
#计算这些数据的平均值(axis=0:求列的均值),作为该类质心向量
centroids[cent,:] = mean(ptsInClust, axis=0)
#返回k个聚类,聚类结果与误差
return centroids, clusterAssment
"""
函数说明:
绘制散点函数
"""
def paint(xArr,yArr,xArr1,yArr1):
fig = plt.figure()
ax = fig.add_subplot(111)
#散点(xArr,yArr)
ax.scatter(xArr,yArr,c='blue')
#质心(xArr1,yArr1)
ax.scatter(xArr1,yArr1,c='red')
plt.show()
"""
函数说明:
二分k-均值聚类算法
"""
def biKmeans(dataSet, k, distMeas=distEclud):
# 返回行数
m = shape(dataSet)[0]
# m x 2 列的矩阵 用来存储每个样本簇系数和误差值
clusterAssment = mat(zeros((m, 2)))
# 获取各列的均值
centroid0 = mean(dataSet, axis=0).tolist()[0]
# 存储簇质心
centList = [centroid0]
# 遍历每个数据样本 返回每个样本到指定簇中心的距离
for j in range(m):
# 计算当前聚为一类时各个数据点距离质心的平方距离
clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :]) ** 2
# 循环,直至二分k-均值达到k类为止
while (len(centList) < k):
# 将当前最小平方误差置为正无穷
lowestSSE = inf
# 遍历当前每个聚类
for i in range(len(centList)):
# 通过数组过滤筛选出属于第i类的数据集合
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :]
# 对该类利用二分k-均值算法进行划分,返回划分后结果,及误差
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
# 计算该类划分后两个类的误差平方和
sseSplit = sum(splitClustAss[:, 1])
# 计算数据集中不属于该类的数据的误差平方和
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])
# 划分第i类后总误差小于当前最小总误差
if (sseSplit + sseNotSplit) < lowestSSE:
# 第i类作为本次划分类
bestCentToSplit = i
# 第i类划分后得到的两个质心向量
bestNewCents = centroidMat
# 复制第i类中数据点的聚类结果即误差值
bestClustAss = splitClustAss.copy()
# 将划分第i类后的总误差作为当前最小误差
lowestSSE = sseSplit + sseNotSplit
# 数组过滤筛选出本次2-均值聚类划分后类编号为1数据点,将这些数据点类编号变为 当前类个数+1,作为新的一个聚类
bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)
# 同理,将划分数据集中类编号为0的数据点的类编号仍置为被划分的类编号,使类编号连续不出现空缺
bestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit
# 更新质心列表中的变化后的质心向量
centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0]
# 添加新的类的质心向量
centList.append(bestNewCents[1, :].tolist()[0])
# 更新clusterAssment列表中参与2-均值聚类数据点变化后的分类编号,及数据该类的误差平方
clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0], :] = bestClustAss
# 返回聚类结果
return mat(centList), clusterAssment
if __name__ == '__main__':
dataMat = np.mat(loadDataSet('testSet.txt'))
centroids,clusterAssment = biKmeans(dataMat, 3)
xArr = dataMat[:,0].flatten().A[0]
yArr = dataMat[:,1].flatten().A[0]
xArr1 = centroids[:,0].flatten().A[0]
yArr1 = centroids[:,1].flatten().A[0]
#进行数据的可视化
paint(xArr,yArr,xArr1,yArr1)

我们可以看出经过二分K-均值聚类算法多次划分后,这次的聚类效果十分令人满意
八. 实战项目:对于地理数据应用二分K-均值聚类算法
1. 步骤:
-
收集数据:使用Yahoo! placeFinder API收集数据。
-
准备数据:只保留经纬度信息。
-
分析数据:使用matplotlib来构建一个二维数据图,其中包含簇与地图。
-
训练算法:训练不适用无监督学习。
-
测试算法:使用上篇中的bikmeans()函教。
-
使用算法:最后的输出是包含簇及簇中心的地图
既然我手头上就有地理位置的文本数据集,我就不使用API来获取数据的了。
2. 代码的逐步实现
球面距离计算
"""
函数说明:
根据公式返回地球表面两点间的距离
"""
def distSlC(vecA, vecB):
a = sin(vecA[0,1]*pi/180) * sin(vecB[0,1]*pi/180)
b = cos(vecA[0,1]*pi/180) * cos(vecB[0,1]*pi/180) * cos((vecB[0,0] - vecA[0,0])*pi/180)
return arccos(a+b)*6371.0
- 单位球面上A,B两点的距离公式
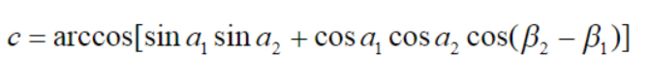
因为我们是计算地球上的距离,那么毋庸置疑 距离=c*地球的半径。
又因为数据集中的经度和纬度都是用角度来作为单位,但是sin函数以弧度来输入。
聚类及簇绘图函数
clusterClubs只有一个参数即所希望得到的簇数目
并且封装了三个函数
-
文本解析
-
聚类
-
画图
"""
函数说明:
聚类及簇绘图函数
打开places.txt文件获取第4列和第5列,分别对应纬度和经度。
基于这些经纬度对的列表创建一个矩阵。
在这些数据点上运行biKmeans()
使用distSLC()函数作为聚类中使用的距离计算方法。
最后将簇以及簇质心画在图上
"""
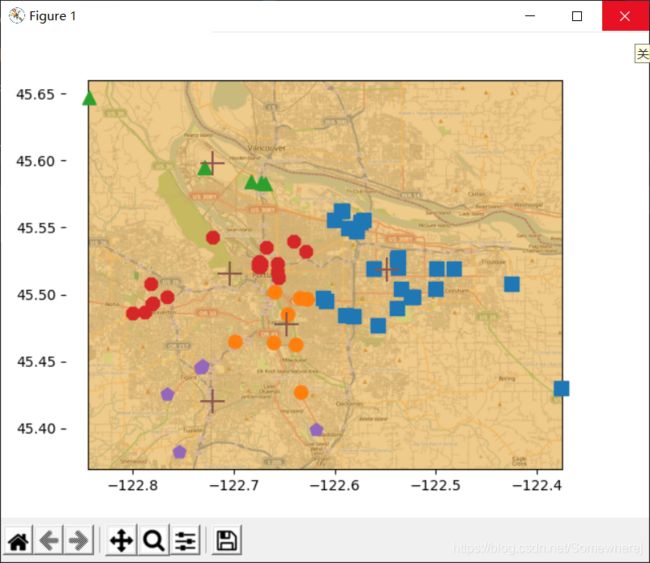
def clusterClubs(numClust=5):
datList = []
for line in open('places.txt').readlines():
lineArr = line.split('\t')
datList.append([float(lineArr[4]), float(lineArr[3])])
datMat = np.mat(datList)
myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSlC)
fig = plt.figure()
rect=[0.1,0.1,0.8,0.8]
scatterMarkers=['s', 'o', '^', '8', 'p', \
'd', 'v', 'h', '>', '<']
axprops = dict(xticks=[], yticks=[])
ax0=fig.add_axes(rect, label='ax0', **axprops)
#看每个人的文本存在哪里
imgP = plt.imread(r'C:\Users\Somewhere\Pictures\蜂蜜浏览器\机器学习实战源代码.rar-machinelearninginaction-Ch10-Portland.png')
ax0.imshow(imgP)
ax1=fig.add_axes(rect, label='ax1', frameon=False)
for i in range(numClust):
ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)
ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300)
plt.show()
整体代码如下
import matplotlib
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
"""
函数说明:
文本文件的解析函数
加载数据集
"""
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = list(map(float,curLine))
dataMat.append(fltLine)
return dataMat
"""
函数说明:
根据公式返回地球表面两点间的距离
"""
def distSlC(vecA, vecB):
a = sin(vecA[0,1]*pi/180) * sin(vecB[0,1]*pi/180)
b = cos(vecA[0,1]*pi/180) * cos(vecB[0,1]*pi/180) * cos((vecB[0,0] - vecA[0,0])*pi/180)
return arccos(a+b)*6371.0
"""
函数说明:
为给定数据集构建一个包含k个随机质心的集合
随机质心必须要在整个数据集的边界之内,可以通过找到数据集每一维的最小和最大值来完成
创建k个点作为起始质心,可以随机选择(位于数据边界内)
当任意一个点的簇分配结果发生改变时
对数据集中每一个点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
"""
def randCent(dataSet, k):
#获取数据集中的坐标维度
#得到n=2
n = shape(dataSet)[1]
#初始化为一个(k,n)的矩阵保存随机生成的k个质心
centroids = mat(zeros((k,n)))
#遍历数据集的每一维度
for j in range(n):
#获取该列的最小值
minJ = min(dataSet[:,j])
#获取该列的最大值
maxJ = max(dataSet[:,j])
#得到该列数据的范围(最大值-最小值)
rangeJ = float(max(dataSet[:,j]) - minJ)
# k个质心向量的第j维数据值随机为位于(最小值,最大值)内的某一值
centroids[:,j] = minJ + rangeJ * random.rand(k,1)
return centroids
"""
函数说明:
k-means 聚类算法
该算法会创建k个质心,然后将每个点分配到最近的质心,再重新计算质心。
这个过程重复数次,直到数据点的簇分配结果不再改变位置。
"""
def kMeans(dataSet, k, distMeas=distSlC, createCent=randCent):
#返回行数
m = shape(dataSet)[0]
#创建一个与dataSet行数一样,但是有两列的m*2矩阵,用来保存簇分配结果
clusterAssment = mat(zeros((m, 2)))
#createCent=randCent,既然都使用randCent了,那就是创建随机k个质心
centroids = createCent(dataSet, k)
#聚类结果是否发生变化的布尔类型
clusterChanged = True
while clusterChanged:
#聚类结果是否发生变化置为false
clusterChanged = False
#遍历数据集每一个样本向量
#循环每一个数据点并分配到最近的质心中去
for i in range(m):
#初始化最小距离最正无穷
minDist = inf
#最小距离对应索引为-1
minIndex = -1
#依次循环k个质心
for j in range(k):
#计算某个数据点到质心的距离,欧式距离
distJI = distMeas(centroids[j,:],dataSet[i,:])
#如果距离比minDist(最小距离)还小
if distJI < minDist:
#更新minDist(最小距离)和最小质心的index(索引)
minDist = distJI
minIndex = j
#当前聚类结果中第i个样本的聚类结果发生变化:
if clusterAssment[i, 0] != minIndex:
#布尔类型置为true,继续聚类算法
clusterChanged = True
#更新簇分配结果为最小质心的 index(索引),minDist(最小距离)的平方
clusterAssment[i, :] = minIndex,minDist**2
#打印k-均值聚类的质心
print(centroids)
#遍历每一个质心
for cent in range(k):
#获取该簇中的所有点
#将数据集中所有属于当前质心类的样本通过条件过滤筛选出来
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A==cent)[0]]
#将质心修改为簇中所有点的平均值,mean 就是求平均值的
#计算这些数据的平均值(axis=0:求列的均值),作为该类质心向量
centroids[cent,:] = mean(ptsInClust, axis=0)
#返回k个聚类,聚类结果与误差
return centroids, clusterAssment
"""
函数说明:
二分k-均值聚类算法
"""
def biKmeans(dataSet, k, distMeas=distSlC):
# 返回行数
m = shape(dataSet)[0]
# m x 2 列的矩阵 用来存储每个样本簇系数和误差值
clusterAssment = mat(zeros((m, 2)))
# 获取各列的均值
centroid0 = mean(dataSet, axis=0).tolist()[0]
# 存储簇质心
centList = [centroid0]
# 遍历每个数据样本 返回每个样本到指定簇中心的距离
for j in range(m):
# 计算当前聚为一类时各个数据点距离质心的平方距离
clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :]) ** 2
# 循环,直至二分k-均值达到k类为止
while (len(centList) < k):
# 将当前最小平方误差置为正无穷
lowestSSE = inf
# 遍历当前每个聚类
for i in range(len(centList)):
# 通过数组过滤筛选出属于第i类的数据集合
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :]
# 对该类利用二分k-均值算法进行划分,返回划分后结果,及误差
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
# 计算该类划分后两个类的误差平方和
sseSplit = sum(splitClustAss[:, 1])
# 计算数据集中不属于该类的数据的误差平方和
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])
# 划分第i类后总误差小于当前最小总误差
if (sseSplit + sseNotSplit) < lowestSSE:
# 第i类作为本次划分类
bestCentToSplit = i
# 第i类划分后得到的两个质心向量
bestNewCents = centroidMat
# 复制第i类中数据点的聚类结果即误差值
bestClustAss = splitClustAss.copy()
# 将划分第i类后的总误差作为当前最小误差
lowestSSE = sseSplit + sseNotSplit
# 数组过滤筛选出本次2-均值聚类划分后类编号为1数据点,将这些数据点类编号变为 当前类个数+1,作为新的一个聚类
bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)
# 同理,将划分数据集中类编号为0的数据点的类编号仍置为被划分的类编号,使类编号连续不出现空缺
bestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit
# 更新质心列表中的变化后的质心向量
centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0]
# 添加新的类的质心向量
centList.append(bestNewCents[1, :].tolist()[0])
# 更新clusterAssment列表中参与2-均值聚类数据点变化后的分类编号,及数据该类的误差平方
clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0], :] = bestClustAss
# 返回聚类结果
return mat(centList), clusterAssment
"""
函数说明:
聚类及簇绘图函数
打开places.txt文件获取第4列和第5列,分别对应纬度和经度。
基于这些经纬度对的列表创建一个矩阵。
在这些数据点上运行biKmeans()
使用distSLC()函数作为聚类中使用的距离计算方法。
最后将簇以及簇质心画在图上
"""
def clusterClubs(numClust=5):
datList = []
for line in open('places.txt').readlines():
lineArr = line.split('\t')
datList.append([float(lineArr[4]), float(lineArr[3])])
datMat = np.mat(datList)
myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSlC)
fig = plt.figure()
rect=[0.1,0.1,0.8,0.8]
scatterMarkers=['s', 'o', '^', '8', 'p', \
'd', 'v', 'h', '>', '<']
axprops = dict(xticks=[], yticks=[])
ax0=fig.add_axes(rect, label='ax0', **axprops)
#看每个人的文本存在哪里
imgP = plt.imread(r'C:\Users\Somewhere\Pictures\蜂蜜浏览器\机器学习实战源代码.rar-machinelearninginaction-Ch10-Portland.png')
ax0.imshow(imgP)
ax1=fig.add_axes(rect, label='ax1', frameon=False)
for i in range(numClust):
ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)
ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300)
plt.show()
if __name__ == '__main__':
clusterClubs(5)
九.总结
-
聚类是一种无监督的学习方法。没有目标变量=目标类别未知
-
聚类将数据点归到多个簇中,其中相似的数据点归为同一簇,而不相似的点归为不同的簇。简单理解就是差不多的才聚在一起,人以群分,物以类聚
-
相似度的计算方法有很多,具体的应用选择合适的相似度计算方法
-
K-means算法虽然有效,但是容易受到初始簇质心的情况而影响,有可能陷入局部最优解。我们可以使用另外一种称为二分K-means的聚类算法,毕竟全局最优效果肯定比局部最优好。经过实验,我们也可以发现二分K-均值聚类算法的聚类效果要好于普通的K-均值聚类算法 。