【机器学习】聚类算法中的 K-means 算法及其原理
系列文章目录
第十四章 Python 机器学习入门之聚类算法
目录
系列文章目录
前言
一、什么是聚类
二、K-means 聚类算法的直观理解
三、K-means 聚类算法公式
四、K-means 聚类算法的优化目标(失真函数J)
五、 K-means 的初始化
六、 选择聚类数量
前言
聚类( clustering )是一种典型的“无监督学习”,是把物理对象或抽象对象的集合分组为由彼此类似的对象组成的多个类的分析过程。K-means 算法是就是比较经典的聚类算法,使用较多,本文主要讲解了什么是K-means 算法及其原理。
一、什么是聚类
聚类 clustering
聚类算法着眼于数据点的数量 和自动查找彼此相关 或相似的数据点。
聚类算法是一种无监督的学习算法。
回想一下我们之前学的用于二元分类的监督学习。如图
给定一个具有特征x_1 和x_2 的数据集,通过监督学习,
我们有一个训练集,输入特征x 以及标签y 。
我们可以绘制出数据集并拟合逻辑回归算法 或用一个神经网络来学习这样的决策边界。
在监督学习中,数据集既包括输入x,也包括目标输出y 。
上面讲的是监督学习,现在来看看无监督学习unspervised learning
我们要求算法找出有关数据的有趣内容(相关联的内容)。
聚类算法clustering 就是一种无监督学习的算法,它会找到数据的一种特定类型的结构。
给定像上图这样未标记的数据集(只有x), 算法就可能会找到有关数据的特定结构,它会查看数据,并尝试查看是否可以将其分组为集群,表示彼此相似的点组,可能会将数据分为两类。
聚类算法的应用有很多,像把类似的新闻文章放在一起,将学习者进行分类等。聚类也被应用于分析DNA 数据。
二、K-means 聚类算法的直观理解
K-means 是使用频率非常多的聚类算法。
先来看看什么是K-means 聚类算法。
如果我们有一个数据集(有30个未标记的训练示例),并对它使用K-means 聚类算法。
K-means 算法做的第一件事是 会随机猜测哪里可能是我们想要它找到的2个集群的中心的位置(想让它找到几个集群我们可以人为决定),它可能就会将数据分为两个集群。
首先K-means 算法会在数据集中找到两个点,如图中的两个点红十字和蓝十字,它其实并不是很好,不过没有关系。
K-means 将反复执行两个步骤,第一个步骤是 将点分给集群质心,第二个步骤是 移动集群质心。
K-means 做的第一件事是随机猜测集群的中心在哪。对于上面的第一个步骤,它会遍历每个数据点并查看它是否更接近红十字或蓝十字。
这些数据可以称为是簇,簇的中心称为簇质心(cluster centroids),换种说法,在对集群质心的位置进行初步猜测后,它会遍历所有的这些示例,从x1 到x30, 也就是所有的数据,它会检查是否有更接近红色的簇质心(图中的红十字或蓝十字)。它会将这些点中的每一个分配给它更接近的集群质心。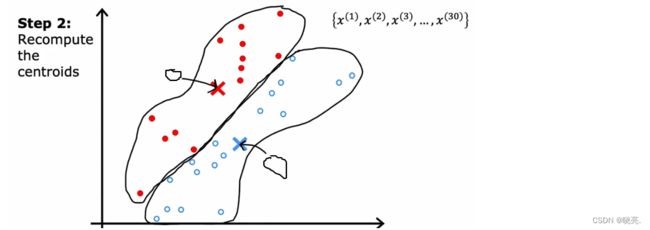
K-means 执行的第二个步骤是移动集群质心,它会查看所有红点并取它们的平均值,然后将红十字移动到红点的平均位置。对蓝十字也是做同样的事情。移动后,我们就会得到两个新的集群质心位置。
接着,重复上面两步。第一步,我们会再次查看所有的30个训练示例,检查它们是否更接近新位置的红色或蓝色簇质心,再将这些点中的每一个分配给它更接近的集群质心。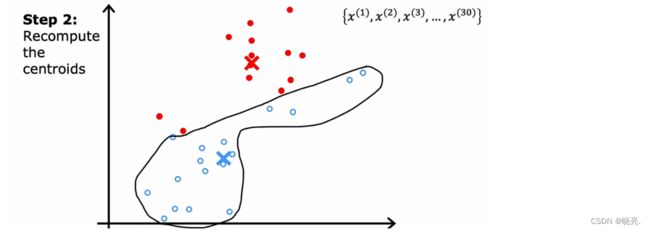
第二步,我们查看所有红点并计算平均值,然后将红十字移动到红点的平均位置。对蓝十字也是做同样的事情。移动后,我们又会得到两个新的集群质心位置。
重复上面两个步骤,直到簇质心的位置或集群质心的位置不再发生改变,这意味着 K-means 聚类算法收敛了,我们最终会得到下图,上面红色对应有关簇,下面的蓝色代表另一个簇。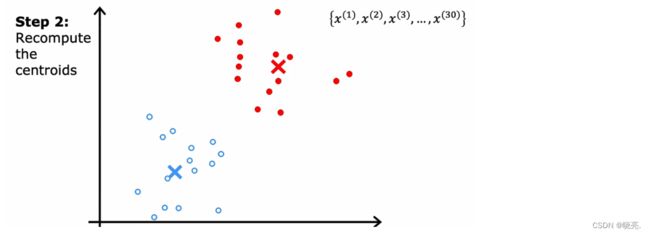
三、K-means 聚类算法公式
我们现在知道了 K-means 聚类算法就是干两件事。
第一件事,初始化K 个簇质心,μ1,μ2一直到μK。(相当于前面所的随机选择的红十字和蓝十字)
前面的例子中分为两个簇质心,也就是红十字和蓝十字,那就可以用μ1,μ2来表示了。(假设红十字是μ1,蓝十字是μ2)
注意:μ1,μ2具有与训练示例相同的维度。我们的30个训练示例中,都是两个数的列表,或者说是二维向量,因为对于每个训练示例,我们有两个特征X1、X2。其中μ1,μ2也是二维向量(表示其中包含两个数字的向量)。
第二件事, K-means 将重复上面提到的 两个步骤 将点分给集群质心,再移动集群质心。
1 将点分给集群质心,对每个训练数据根据离 簇质心 的距离进行分类(红色或蓝色)。
每个训练数据点x 与质心μ 的距离,也被称为L2 范数。我们想要的就是找到这个最小化这个距离 K 。
然后将最小化的K值设置为图中的C_i, 其实这个距离 更方便的是写成平方距离,最小化平方距离与最小化的簇质心是相同的。
2 移动集群质心,计算所有红点的平均值,水平轴平均值、垂直轴平均值,两条的交点就是更新后红色簇质心的位置。对蓝色的簇质心也是相同的操作。
如果第一个红色集群已经分配了训练示例x1,x5, x6, x10 ,计算平均值的公式如图所示。
这里我们有两个特征,所以我们的μ 中有两个数字也就是二维向量,如果我们有n 个特征,那么我们的μ 就有n 个数,是n 维向量。
如果示例出现极端情况,训练后,一个集群里面有0个训练示例,那么算法会在第二步计算0 的平均值。
这种情况我们一般会直接取消该集群,最终会得到K-1 个簇(这是常见做法) 。
如果需要K个簇,那么一个方法就是重新初始化该集群的质心,使得它在下一轮的循环中得到一些训练示例。
除了上面说的,K-means算法也可以很好的处理集群没有很好分离的数据集。比如说将一堆连着的数据进行分类。
四、K-means 聚类算法的优化目标(失真函数J)
为了保证 K-means 聚类算法会收敛,我们需要求代价函数了。 
我们会使用到c_i, 它指训练示例x_i 与集群质心的距离,并判断x_i 离哪一个集群质心近,然后就分配给哪个集群质心。
μ_k 是簇质心的位置
μ_ki 是指已经分配训练示例xi 的集群质心的位置。
上面就是 K-means算法的代价函数,我们需要的就是最小化的平方距离,也就是最小化代价函数。
这里的代价函数它也叫做失真函数 distortion,
下面我们来进一步的学习这个失真函数 J
K-means的第一部分表示将训练数据点分配给集群质心的位置,也就是改变c1,c2…cm 来降低失真函数 J。 具体来讲,就是让每个数据点选择离自己最近的一个聚类中心。像图中的黑点,它就会选择红十字。
第二部分就是移动集群质心位置。
K 中的每一步都在设置值c_i 和 μ_k 来试图降低代价函数。
五、 K-means 的初始化
K-means 聚类算法的第一步就是选择随机位置作为集群质心。
为了选择集群质心,最常见的方法是随机选择k 个训练样例。这与前面提到的有些不同,前面是随机选择初始的集群质心,选择是随机选择训练样例。
如图这是一个训练集,如果随机选择两个训练示例,来作为初始的集群质心,可能会选择图中画圈的,
如果只想分类两个集群,那么就只有μ1,μ2两个集群质心,如图,就可以将一个点设置为一开始的红十字,另一个点设置为蓝十字的位置,着两个点就是一开始的集群质心。
再次强调,这里与前面将的有些不同,前面一开始的集群质心是随机选取的,这里是放在特定的训练示例上,事实证明,这种方法是初始化集群质心的常用方法。
选择是随机选择训练样例作为初始的集群质心 虽然比 随机选择任意点作为初始的集群质心要好。但是,这一会出一些问题,如图,它可能出现局部最优值。
这种效果不好的情况,我们就要运行多次,来找到最佳的局部最优值,如图中的3种,我们可以选择最上面的那个来为我们提供代价函数 J 的最低值。
将上面思想写成算法
假设我们想使用100 个随机初始化 K-means, 那就会随机初始化运行100次,
首先随机选择一个示例位置作为初始的集群质心,计算代价函数,运行100次,选择最小的代价函数值。(一般这个次数在50-1000这个范围都合理的)
这就是为什么我们一般会使用多个初始化,因为会计算出多个最小化代价函数,可以为集群质心找到更好的选择。
六、 选择聚类数量
K-means 算法需要k 作为其输入之一,也就是我们希望它找到的集群数量。
如何来选择k 的值呢,有人提出使用elbow 方法,也就是肘部方法,他的意思就是将代价函数看成是集群数量的函数,看看曲线是否有弯曲,如图,k = 3 是个转折点,k 大于3,代价函数就下降的很慢了,所以就选择k= 3,因为形状看起来很像肘部,所以就被称为肘部算法了。
但是这种方法有局限性,如果代价函数下降平滑,就像右边的图,我们就找不到任何的肘点了。
注意:使用k 来最小化J 也是不行的,因为代价函数J 的值会随着k 越多而越小的,所以这种方法不可取。
如图中的例子,我们可能会纠结K = 3 还是5,一般情况,我们会运行这两种情况,权衡各种因素,来选择使用哪个。
k-means 的应用很广泛,它还可以使用在图片压缩方面。





