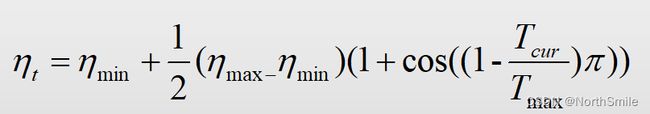Pytoch优化器常用的两种学习率衰减策略:指数衰减策略、余弦退火策略(附测试代码)
学习率衰减策略
- 前言
- 一、指数衰减策略(ExponentialLR)
-
- 1.介绍
- 2.调用方式
- 3.使用案例
- 二、余弦退火策略(Cosine Annealing)
-
- 1.介绍
- 2.调用方式
- 3.使用案例
- 三、测试案例
- 参考:
前言
网络训练过程中,学习率不能过大,也不能过小,学习率过大会导致网络参数在最优值两边来回跳跃,难以收敛,学习率太小会导致网络收敛过慢,所以我们一般希望网络训练前期学习率较大可以加速网络收敛,后期学习率较小,以此使得网络更收敛于最优值。为了控制学习率,研究者提出了多种衰减策略。Pytorch内部提供了常见的多种学习率衰减策略,我在这里介绍常用的指数衰减策略和余弦退火策略,并分别介绍他们的代码实现。
无论采用那种策略,在网络训练之间我们均需要进行以下两步工作:
1)创建优化器Optimizer;
2)为优化器绑定一个学习率控制器Scheduler;
一、指数衰减策略(ExponentialLR)
1.介绍
指数衰减策略是比较常用也比较基础的学习率调整策略,以底数λ∈(0,1)的指数函数的形式控制学习率的变化,令其逐渐变小。
底数在(0,1)范围内的指数函数曲线如下:
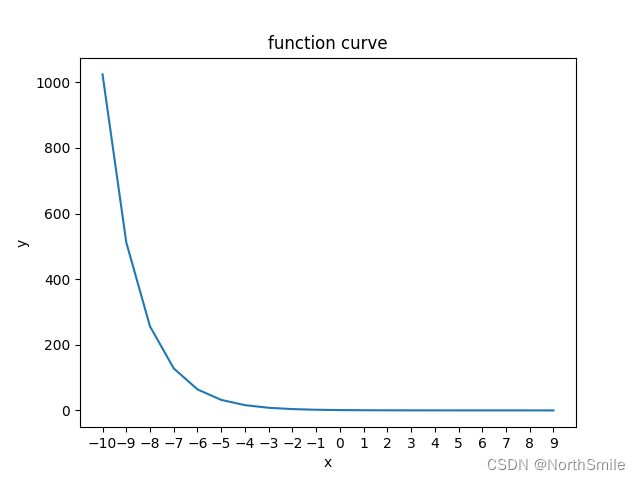
我们需要知道,指数衰减策略以网络对训练集的每轮完整训练作为变化周期,既每个epoch过后学习率都进行一次调整。公式中decay_lr和current_lr分别表示衰减后的学习率和当前学习率,λ表示衰减因子,epoch表示第几次调整学习率,其中我们需要设置的是衰减系数λ,该因子可以控制学习率以不同的方式去进行调整。
下图是几种不同衰减因子λ对应的学习率衰减图:
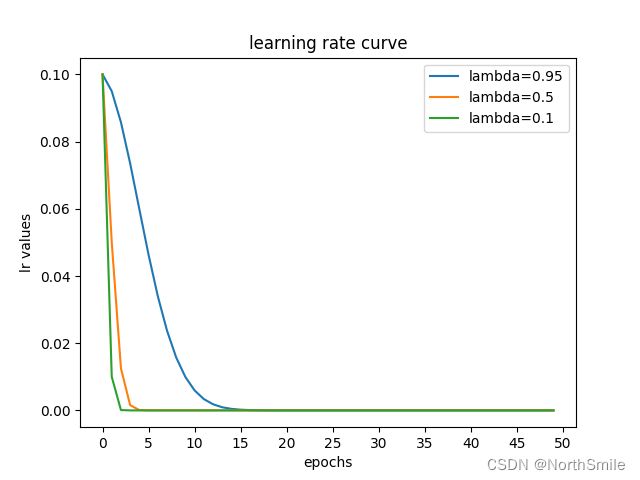
对上图做一个解释:
初始学习率learning_rate=0.1,衰减因子λ=lambda2=0.5,一共训练50个epoch,每个epoch后调整一次学习率,因此学习率共调整50次,调整过程依次为:
- epoch=0,current_lr=0.1,decay_lr=current_lr×λ1=0.1×0.5=0.05;
- epoch=1,current_lr=0.5,decay_lr=current_lr×λ2=0.05×0.5=0.025;
- epoch=2,current_lr=0.025,decay_lr=current_lr×λ3=0.025×0.5=0.0125;
- …依次类推,共更新学习率50次;
2.调用方式
torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=- 1, verbose=False)
其中gamma参数就是公式中所说的衰减因子,我们需要设置的参数主要就是该参数。
3.使用案例
creation=nn.CrossEntropyLoss()
creation=creation.to(device)
optimizer=torch.optim.Adam(params=model.parameters(),lr=0.1,betas=(0.9, 0.999))
scheduler=torch.optim.lr_scheduler.ExponentialLR(optimizer,gamma=0.5)
for epoch in range(10):
# training
print("-----")
print("epoch:",epoch)
for batch,(img,label) in enumerate(train_dataloader):
img, label=img.to(device),label.to(device)
prediction=model(img)
loss=creation(prediction,label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
scheduler.step() # 调整学习率
二、余弦退火策略(Cosine Annealing)
1.介绍
余弦函数图示:
https://arxiv.org/pdf/1608.03983.pdf一文提出带有热启动的随机梯度下降法:Stochastic Gradient Descent With Warm Restarts(SGDR),其中就引入了使用余弦退火策略进行学习率调整,此时学习率不像指数衰减策略一样一直下降,而是在每个周期内“先下降,再上升”。结合余弦退火策略进行动态调整学习率是利用余弦函数前半周期“先缓慢下降,再快速下降,然后继续缓慢下降”的特性,使得网络训练刚开始可以快速收敛,后期缓慢收敛以更接近最优解。
下图描述了最简单的热启动方法的工作原理:

| 参数 | 含义 |
|---|---|
| i | 表示学习率调整周期的索引(同余弦函数周期的概念) |
| Ti | 每个调整周期内epochs的总数,论文中每次是改变的,简单起见,可将其固定不变 |
| η imin | 表示学习率的最小值,简单起见设置为0 |
| η imax | 表示学习率的最大值,简单起见设置为初始学习率 |
| Tcur | 记录学习率最近一次重启后,到现在经过了多少epochs |
在每个epoch中都有多个batch=len(dataset)/batch_size,而Tcur在每个batch过后都会改变,所以Tcur可以为小数,比如我们期望网络总共训练50个epoch,训练集长度为320,batch_size为32,设置Ti=50,每个epoch中共进行320/32=10个batch的的迭代,所以Tcur的取值可以为1/10,2/10,…,,10/10,可进一步这样理解:此时一共有50×10=500个batch,Tcur依次从0到500。
从上述公式中可以看到当Tcur=Ti时η t取得最小值;而Tcur=0时η t取得最大值。
下图中绿色曲线即为我们这里说的固定Ti=50的情况,余弦函数的自变量取值范围为[0,π]。

1)余弦退火策略
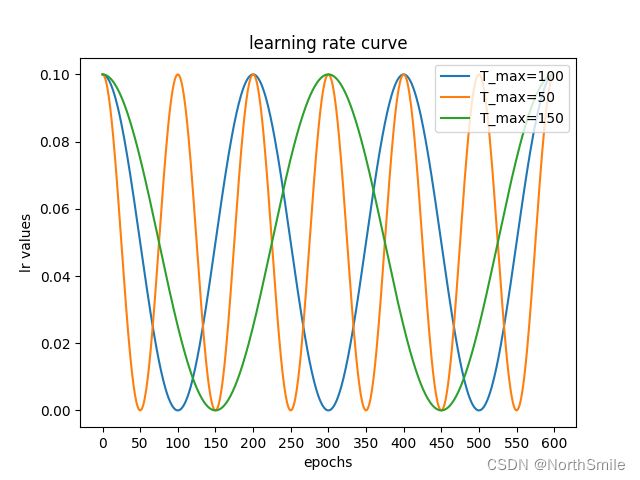
了解了上面提到的带有热启动的梯度下降算法后,我们看一下最朴素的余弦退火策略进行学习率衰减,这种方法不进行热启动,余弦函数的自变量取值范围为[0,2π],此时学习率在一个周期内完全按照余弦函数的变化取值进行。通常我们需要调整的是参数Tmax,此处Tmax可将其理解为余弦函数的半周期,即此时学习率变化的周期为2Tmax。类似余弦函数的变化趋势,此时学习率在前半周期先下降,后半周期逐渐上升。此时Tcur可理解为周期为Tmax中的每个epoch,比如Tmax=5,则Tcur依次取0,1,…,5即可。
前半周期更新公式:
2.调用方式
torch.optim.lr_scheduler.CosineAnnealingLR(
optimizer,
T_max,
eta_min=0,
last_epoch=- 1,
verbose=False)
此处我们平常需要设置的参数主要是T_max,可将其理解为余弦函数的半周期,比如T_max=5,则表示余弦函数的周期为10。
3.使用案例
creation=nn.CrossEntropyLoss()
creation=creation.to(device)
optimizer=torch.optim.Adam(params=model.parameters(),lr=0.1,betas=(0.9, 0.999))
scheduler=torch.optim.lr_scheduler.CosineAnnealingLR(optimizer,T_max=5)
lr_list=[]
for epoch in range(30):
# training
print("-----")
print("epoch:",epoch)
for batch,(img,label) in enumerate(train_dataloader):
img, label=img.to(device),label.to(device)
prediction=model(img)
loss=creation(prediction,label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
scheduler.step() # 调整学习率
三、测试案例
1)这里所举例子,采用Adam优化器,学习率调整采用指数衰减策略,且gamma=0.5。
import numpy as np
import torch
import torch.nn as nn
from matplotlib.ticker import MultipleLocator
from torch.utils.data import Dataset,DataLoader
from matplotlib import pyplot as plt
from torchvision import transforms,datasets
import warnings
warnings.filterwarnings('ignore')
device=torch.device("cuda" if torch.cuda.is_available() else "cpu")
print("current device:",torch.cuda.get_device_name(device))
train_dataset=datasets.MNIST(
root='./data',
train=False,
transform=transforms.ToTensor(),
download=True)
print("length of train_dataset",len(train_dataset)) # 60000
train_dataloader=DataLoader(
dataset=train_dataset,
batch_size=32,
shuffle=False,
num_workers=0,
drop_last=False
)
class DemoModel(nn.Module):
def __init__(self):
super(DemoModel, self).__init__()
self.model1=nn.Sequential(
nn.Flatten(),
nn.Linear(28*28,512),
nn.Linear(512, 128),
nn.Linear(128, 32),
nn.Linear(32, 10),
nn.Softmax()
)
def forward(self,x):
return self.model1(x)
model=DemoModel()
model=model.to(device)
creation=nn.CrossEntropyLoss()
creation=creation.to(device)
optimizer=torch.optim.Adam(params=model.parameters(),lr=0.1,betas=(0.9, 0.999))
scheduler=torch.optim.lr_scheduler.ExponentialLR(optimizer,gamma=0.5)
lr_list=[]
for epoch in range(10):
# training
print("-----")
print("epoch:",epoch)
for batch,(img,label) in enumerate(train_dataloader):
img, label=img.to(device),label.to(device)
prediction=model(img)
loss=creation(prediction,label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
current_lr = optimizer.state_dict()['param_groups'][0]['lr'] # 当前学习率
lr_list.append(current_lr)
print("current_lr:",current_lr)
scheduler.step() # 调整学习率
adjusted_lr = scheduler.get_last_lr()
print("adjusted_lr:",adjusted_lr)
print("-----")
index_list=np.linspace(0,9,10)
figure,axes=plt.subplots()
axes.set_title("learning rate curve")
axes.plot(index_list,lr_list)
axes.set_xlabel('batch times')
axes.set_ylabel('lr value')
axes.xaxis.set_major_locator(MultipleLocator(1.0))
plt.show()
代码输出结果如下:
current device: GeForce RTX 3090
length of train_dataset 10000
-----
epoch: 0
current_lr: 0.1
adjusted_lr: [0.05]
-----
-----
epoch: 1
current_lr: 0.05
adjusted_lr: [0.025]
-----
-----
epoch: 2
current_lr: 0.025
adjusted_lr: [0.0125]
-----
-----
epoch: 3
current_lr: 0.0125
adjusted_lr: [0.00625]
-----
-----
epoch: 4
current_lr: 0.00625
adjusted_lr: [0.003125]
-----
-----
epoch: 5
current_lr: 0.003125
adjusted_lr: [0.0015625]
-----
-----
epoch: 6
current_lr: 0.0015625
adjusted_lr: [0.00078125]
-----
-----
epoch: 7
current_lr: 0.00078125
adjusted_lr: [0.000390625]
-----
-----
epoch: 8
current_lr: 0.000390625
adjusted_lr: [0.0001953125]
-----
-----
epoch: 9
current_lr: 0.0001953125
adjusted_lr: [9.765625e-05]
-----
训练过程中学习率调整过程如下图所示:

2)除了采用的衰减策略换为余弦退火策略之外,网络训练epochs换为30,将Tmax设置为5,可得如下结果:
可看到此时学习率的调整周期为2Tmax=10,与我们之前分析的结果一致。
scheduler=torch.optim.lr_scheduler.CosineAnnealingLR(optimizer,T_max=5)
这里扩充一个知识点,我们想查看某个时刻的学习率时,可通过下属方式获取:
optimizer.state_dict()['param_groups'][0]['lr']
感兴趣的可以把学习率自己打出来看看!当然我上面的代码实例中也打印了每轮中的学习率。
参考:
https://arxiv.org/pdf/1608.03983.pdf
声明:以上关于余弦退火策略部分内容为自己结合论文及代码理解而来,如有错误,欢迎大家指正!谢谢!