智能计算之遗传算法(GA)介绍

目录

1. 简介

2. GA思想来源及建立过程

3. 研究发展

4. GA的基本结构

5. GA的实现流程

(1) 染色体编​辑

(2) 群体的初始化

(3) 适应值评价

(4) 选择算子(父体选择)

(5) 交配算子(杂交算子)

(6) 变异算子

(7) 算法流程

6. 实例举例

7. 遗传算法的改进

(1) 算子的选择

(2) 参数设置

(3) 混合遗传算法

8. GA的应用

---

1. 简介

        遗传算法（Genetic Algorithm，GA）是进化计算的一个分支，是一种模拟自然界生物进化过程的随机自适应的全局搜索算法。

2. GA思想来源及建立过程

        GA思想源于自然界“自然选择”和“优胜劣汰”的进化规律，通过模拟生物进化中的自然选择和交配变异寻找问题的全局最优解。它最早由美国密歇根大学教授John H. Holland提出，现在已经广泛应用于各种工程领域的优化问题之中。

        GA是通过模拟自然界中生物的遗传进化过程,对优化问题的最优解进行搜索。算法维护一个代表问题潜在解的群体,对于群体的进化,算法引入了类似自然进化中选择、交配以及变异等算子。遗传算法搜索全局最优解的过程是一个不断迭代的过程(每一次迭代相当于生物进化中的一次循环),直到满足算法的终止条件为止。
        在遗传算法中,问题的每个有效解被称为一个“染色体(chromosome)”,在有些书籍中也称为“串”,相对于群体中的每个生物个体(individual)。染色休的具体形式是一个使用特定编码方式生成的编码串。编码串中的每一个编码单元称为“基因(gene)”

如图：

        遗传算法通过比较适应值(fitness value)区分染色体的优劣,适应值越大的染色体越优秀。评估函数(evaluation function)用来计算并确定染色体对应的适应值。

        选择算子按一定的规则对群体的染色体进行选择，得到父代种群。（一般的，越优秀的染色体被选中的次数越多。）

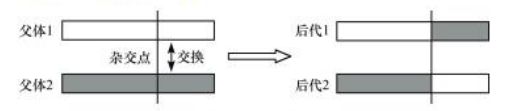
        交配算子作用于每两个成功交配的染色体，染色体交换各自部分的基因，形成两个子代染色体。子代染色体取代父代进入新种群，而没有交配的染色体自动进入新的种群。

        变异算子使得新种群进行小概率的变异。染色体发生变异的基因改变数值，经过变异的新种群替代原种群进入下一次进化。

        对于遗传算法的基本原理,Holland给出了著名的模式定理(Schema Theory),为遗传算法提供了理论支持。
        模式(schema)是指群体中编码的某些位置具有相似结构的染色体集合。假设染色体的编码是由0或1组成的二进制符号序列,模式01***О则表示以01开头且以О结尾的编码串对应的染色体的集合，即{010000,010010,010100,010110,011000,011010,011100,011110}。模式中具有确定取值的基因个数叫做模式的阶(schema order),如模式01***0 的阶为3。模式的定义长度(schema defining length)是指模式中第一个具有确定取值的基因到最后一个具有确定取值的基因的距离,例如模式01***0的定义长度为5,而*1****的定义长度为0。
        Holland 的模式定理提出﹐遗传算法的实质是通过选择、交配和变异算子对模式进行搜索,低阶、定义长度较小且平均适应值高于群体平均适应值的模式在群体中的比例将呈指数级增长,即随着进化的不断进行,较优染色体的个数将快速增加。
        模式定理证明了遗传算法寻求全局最优解的可能性,但不能保证算法一定能找到全局最优解。Goldberg[10]在1989年提出了积木块假设(Building Block Hypothesis),对模式定理做了补充,说明遗传算法具有能够找到全局最优解的能力。
        积木块(building block)是指低阶、定义长度较小且平均适应值高于群体平均适应值的模式。积木块假设认为在遗传算法运行过程中,积木块在遗传算子的影响下能够相互结合,产生新的更加优秀的积木块,最终接近全局最优解。

3. 研究发展

4. GA的基本结构

        遗传算法是美国密歇根(M ichigan)大学的J.H.Holland教授在研究自然界自适应现象的过程中提出来的.Holland所提出的遗传算法常被称为简单遗传算法(SGA)。遗传算法的基本结构如算法2.1所示.

        在算法2.1中,在对规模为N的种群初始化和对种群中个体计算适应值后，按照基于个体适应值的某个概率函数选择N个父体,适应值较大的个体被选择作为父体的可能性较大.通过杂交,N个父体产生N个后代,N个后代以一定的概率进行变异,并都存活下来,形成下一代种群.在遗传算法中,杂交算子是一个主要的遗传算子,而以较小的概率对个体进行变异.

5. GA的实现流程

(1) 染色体编辑

        目前用于染色体编码的方法有格雷码编码、字母编码、多参数交叉编码等。这里仅给出两种常见的较为简单的编码方法：二进制编码方法和浮点数编码方法。 

二进制编码方法

        举一个简单的例子，假设[Umin ,Umax]为[1，64],采用6位二进制符号串进行编码,则某个二进制符号串010101代表了数值22。
        二进制编码操作简单，但当你的L较大时，计算难度会增大，难以解决精度要求高的问题，因此，我们需要寻求另外的编码方法。

(2) 群体的初始化

        一般情况下，遗传算法在群体初始化阶段采用的是随机数初始化方法。采用生成随机数的方法，对染色体的每一维变量进行初始化赋值。初始化染色体时必须注意染色体是否满足优化问题对有效解的定义。

        如果在进化开始时保证初始群体已经是一定程度上的优良群体的话，将能够有效提高算法找到全局最优解的能力。

(3) 适应值评价

        评估函数用于评估各个染色体的适应值，进而区分优劣。评估函数常常根据问题的优化目标来确定，比如在求解函数优化问题时，问题定义的目标函数可以作为评估函数的原型。
        在遗传算法中，规定适应值越大的染色体越优。因此对于一些求解最大值的数值优化问题，我们可以直接套用问题定义的函数表达式。但是对于其他优化问题，问题定义的目标函数表达式必须经过一定的变换。

(4) 选择算子(父体选择)

轮盘赌选择法

         按适应值大小切分区域大小，即适应值越大的染色体占比越大，越有可能被选中，同时由于是随机选取，也保证了适应值小的染色体也有被选中的可能。

(5) 交配算子(杂交算子)

        在染色体交配阶段，每个染色体能否进行交配由交配概率Pc（一般取值为0.4到0.99之间）决定，其具体过程为：对于每个染色体，如果Random(0, 1)小于Pc则表示该染色体可进行交配操作（其中Random(0, 1)为[0, 1]间均匀分布的随机数），否则染色体不参与交配直接复制到新种群中。 

        每两个按照Pc交配概率选择出来的染色体进行交配，经过交换各自的部分基因，产生两个新的子代染色体。具体操作是随机产生一个有效的交配位置，染色体交换位于该交配位置后的所有基因。

注意：因为父代是两个染色体，生成的子代也是两个染色体，故种群染色体总数N值不会改变。

(6) 变异算子

        染色体的变异作用于基因之上，对于交配后新种群中染色体的每一位基因，根据变异概率Pm判断该基因是否进行变异。

        如果Random(0, 1)小于Pm，则改变该基因的取值（其中Random(0, 1)为[0, 1]间均匀分布的随机数）。否则该基因不发生变异，保持不变。

(7) 算法流程

Step 1：初始化规模为N的群体,其中染色体每个基因的值采用随机数产生器生成并满足问题定义的范围。当前进化代数Generation=0。
Step 2：采用评估函数对群体中所有染色体进行评价,分别计算每个染色体的适应值,保存适应值最大的染色体 Best。
Step 3：采用轮盘赌选择算法对群体的染色体进行选择操作,产生规模同样为N的种群。
Step 4：按照概率P从种群中选择染色体进行交配。每两个进行交配的父代染色体,交换部分基因,产生两个新的子代染色体,子代染色体取代父代染色体进入新种群。没有进行交配的染色体直接复制进入新种群。
Step 5：按照概率P。对新种群中染色体的基因进行变异操作。发生变异的基因数值发生改变。变异后的染色体取代原有染色体进入新群体﹐未发生变异的染色体直接进人新群体。
Step 6：变异后的新群体取代原有群体﹐重新计算群体中各个染色体的适应值。倘若群体的最大适应值大于Best的适应值,则以该最大适应值对应的染色体替代 Best。
Step 7：当前进化代数Generation 加1。如果 Generation超过规定的最大进化代数或Best达到规定的误差要求,算法结束;否则返回Step 3。

6. 实例举例

解：

7. 遗传算法的改进

        遗传算法简单,可操作性强,具有较强的健壮性和普适性以及潜在的并行性,并且拥有较好的全局搜索能力,能够以较大的概率得到全局最优解,因此多个领域的复杂问题相继采用了遗传算法进行解决,进而促进了遗传算法理论研究的不断发展。遗传算法从提出到现在不过几十年的时间,成功的应用案例展示了其作为一种随机全局搜索算法的强大优势和能力,同时,在应用中出现的问题也暴露了现有遗传算法的局限和不足。因此,大量的对算法进行改进的研究活动从未停止过,人们一直致力于提高和拓展算法的能力。

我们可以从以下几个方面去进行改进：

(1) 算子的选择

(2) 参数设置

(3) 混合遗传算法

 (4) 并行遗传算法

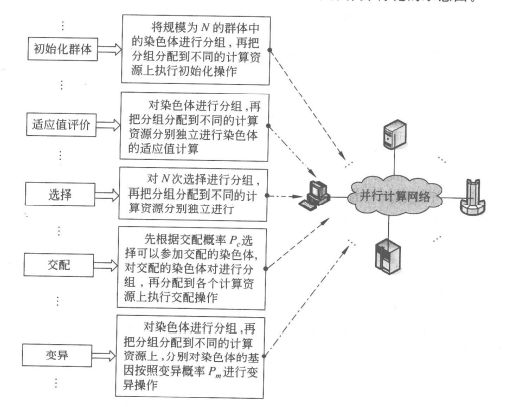
并行遗传算法一般有两种表现形式：标准型并行方法和分解型并行方法。

8. GA的应用

        遗传算法最早用于研究和设计人工自适应系统和求解函数优化问题。随着对遗传算法的研究逐步深入,遗传算法的性能不断地得到改进和完善,算法的应用涉及更加广泛的领域,并表现出很好的解决问题的能力。目前,遗传算法的应用范围已延伸到组合优化,图像处理,模式识别.智能控制,神经网络、自动程序设计、机器学习、人工生命,数据挖掘.网络通信等多个领域和各类学科如电子工程学,电力学、社会学经济学和电磁学等。

洋洋就介绍到这里了，我也是初次学，请大家指教，有问题之间评论或私聊即可，看到就会回复哦，先说好，我不知我什么时候会上线哦，有时候一个星期也不来一次的。哈哈哈！