使用sklearn不同方法在digits手写数字数据集上聚类并用matplotlib呈现
本文内容
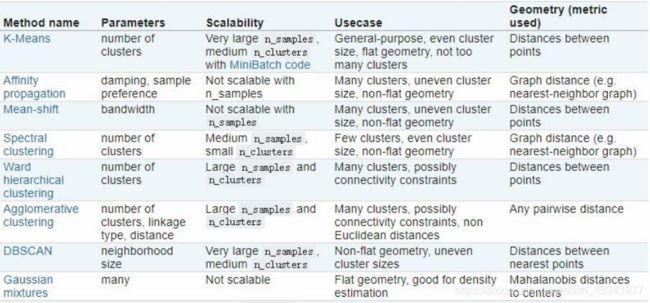
- 测试sklearn中以下聚类算法在digits手写数字数据集上的聚类效果。
- 使用不同的评估方法对实验结果进行评估。
准备
- [ ] sklearn库
自2007年发布以来,scikit-learn已经成为Python重要的机器学习库了,scikit-learn简称sklearn,支持包括分类,回归,降维和聚类四大机器学习算法。还包括了特征提取,数据处理和模型评估者三大模块。
sklearn是Scipy的扩展,建立在Numpy和matplolib库的基础上。利用这几大模块的优势,可以大大的提高机器学习的效率。
sklearn拥有着完善的文档,上手容易,具有着丰富的API,在学术界颇受欢迎。sklearn已经封装了大量的机器学习算法,包括LIBSVM和LIBINEAR。同时sklearn内置了大量数据集,节省了获取和整理数据集的时间。
库的算法主要有四类:分类,回归,聚类,降维。其中:
常用的回归:线性、决策树、SVM、KNN ;集成回归:随机森林、Adaboost、GradientBoosting、Bagging、ExtraTrees
常用的分类:线性、决策树、SVM、KNN,朴素贝叶斯;集成分类:随机森林、Adaboost、GradientBoosting、Bagging、ExtraTrees
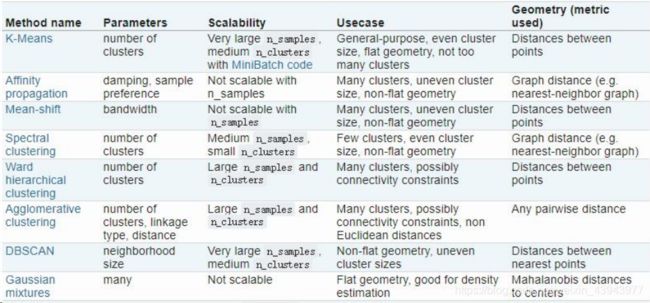
常用聚类:k均值(K-means)、层次聚类(Hierarchical clustering)、DBSCAN
常用降维:LinearDiscriminantAnalysis、PCA
它具有以下特点
- 简单高效的数据挖掘和数据分析工具
- 每个人都可以访问,并且可以在各种情况下重用
- 基于NumPy,SciPy和matplotlib构建
- 开源,可商业使用-BSD许可证
- sklearn datasets
sklearn中包含了大量的优质的数据集,在我们学习机器学习的过程中,我们可以使用这些数据集实现出不同的模型。
首先,要使用sklearn中的数据集,必须导入datasets模块。
from sklearn import datasets
- digits手写数字数据集
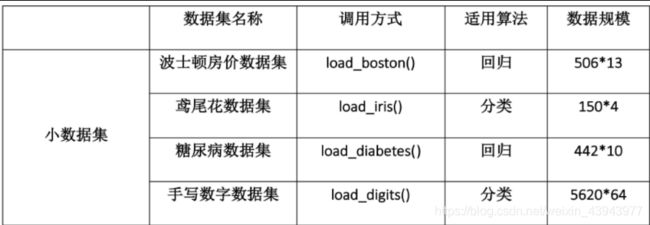
实验要求采用digits数据集,我们先对这个数据集进行一个初步的了解:
手写数字数据集包含1797个0-9的手写数字数据,每个数据由8 * 8 大小的矩阵构成,矩阵中值的范围是0-16,代表颜色的深度。
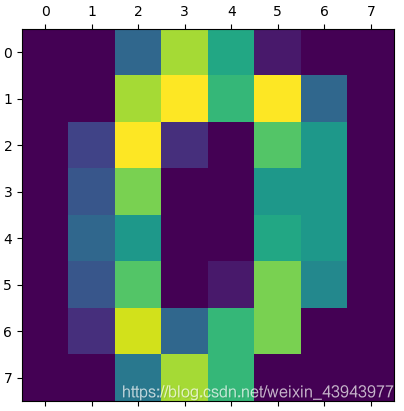
我们先加载一下数据,了解一下数据的维度,并以图像的形式展示一些第一个数据:
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
digits = load_digits()
print(digits.data.shape)
print(digits.target.shape)
print(digits.images.shape)
plt.matshow(digits.images[0])
plt.show()
可以看到数据维度和第一张手写数字
(1797, 64)
(1797,)
(1797, 8, 8)
实验过程
- K-means聚类digits数据集
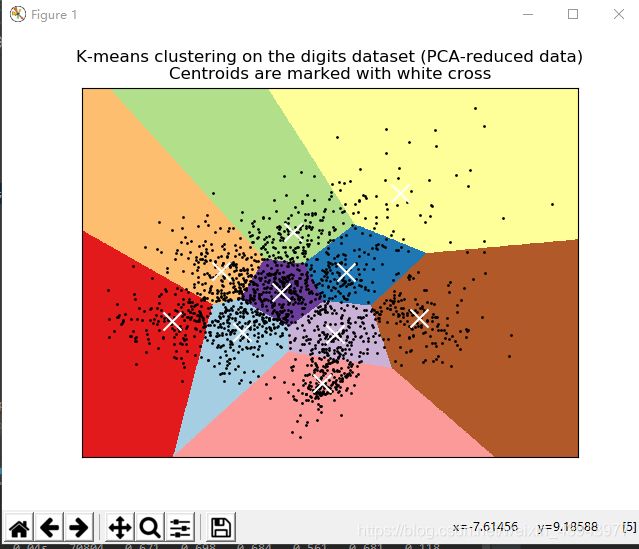
在sklearn官网中提供的K-means对digits的聚类的demo代码中运行出来的结果如下:(链接:https://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_digits.html#sphx-glr-auto-examples-cluster-plot-kmeans-digits-py)
整个可视化的生成很漂亮,细细研究下整个实现过程来发现官方给出的示例也很棒,下面对代码进行分析并进行改动,给出我们通常意义上的直接的聚类效果:
从库sklearn.datasets中加载digits数据集,数据集的介绍见上面。数据集是分好label的,存在digits.target中,同时我们可以提取出数据集的样本数,每个样本的维度,分别存在n_samples n_features中,输出这三个变量,可以得到:
n_digits: 10
n_samples 1797
n_features 64
下面是一段核心评估代码,使用不同的评分方法来计算score表示聚类后类别的准确性,下面再分别用三种k-means聚类的方式来调用这段评分代码,得到不同的score,这也是输出文字的全部内容(ps:这段代码写的真的很漂亮)
def bench_k_means(estimator, name, data):
t0 = time()
estimator.fit(data)
print('%-9s\t%.2fs\t%i\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f'
% (name, (time() - t0), estimator.inertia_,
metrics.homogeneity_score(labels, estimator.labels_),
metrics.completeness_score(labels, estimator.labels_),
metrics.v_measure_score(labels, estimator.labels_),
metrics.adjusted_rand_score(labels, estimator.labels_),
metrics.adjusted_mutual_info_score(labels, estimator.labels_,average_method='arithmetic'),
metrics.silhouette_score(data, estimator.labels_, metric='euclidean',sample_size=sample_size)))
bench_k_means(KMeans(init='k-means++', n_clusters=n_digits, n_init=10),name="k-means++", data=data)
bench_k_means(KMeans(init='random', n_clusters=n_digits, n_init=10),name="random", data=data)
# in this case the seeding of the centers is deterministic, hence we run the
# kmeans algorithm only once with n_init=1
pca = PCA(n_components=n_digits).fit(data)
bench_k_means(KMeans(init=pca.components_, n_clusters=n_digits, n_init=1),name="PCA-based",data=data)
由此得到init=random,k-means++,pca下各个方式的score
init time inertia homo compl v-meas ARI AMI silhouette
k-means++ 0.42s 69432 0.602 0.650 0.625 0.465 0.621 0.146
random 0.22s 69694 0.669 0.710 0.689 0.553 0.686 0.147
PCA-based 0.04s 70804 0.671 0.698 0.684 0.561 0.681 0.118
补充:KMeans函数主要参数:
(这里只列出一部分,详见https://blog.csdn.net/weixin_44707922/article/details/91954734)
- 可视化聚类
其实上面的代码k-means聚类和评估已经全部完成了,但是为了更好可视化输出,我们可以进行如下操作:
pca降维至两维,再次进行聚类,这是因为
1.散点图中的数据点就是两位的
2.在2维的基础上再次k-means聚类是因为已经聚类高维数据映射到二维空间的prelabel可能分散不过集中,影响可视化效果。
reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init='k-means++', n_clusters=n_digits, n_init=10)
kmeans.fit(reduced_data) # 对降维后的数据进行kmeans
result = kmeans.labels_
得到各个类的中心点:
centroids = kmeans.cluster_centers_
最后这一部分就是定义输出的变化范围和输出的效果了
#窗口
plt.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap=plt.cm.Paired,
aspect='auto', origin='lower')
#降维后的数据点
plt.plot(reduced_data[:, 0], reduced_data[:, 1], 'k.', markersize=2)
#聚类中心
plt.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='w', zorder=10)
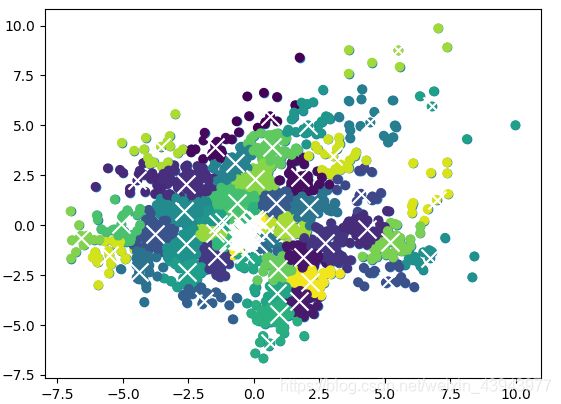
- 对demo可视化效果的修改/另一种形式展示
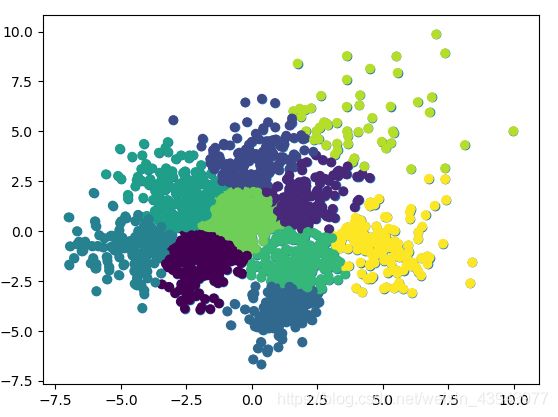
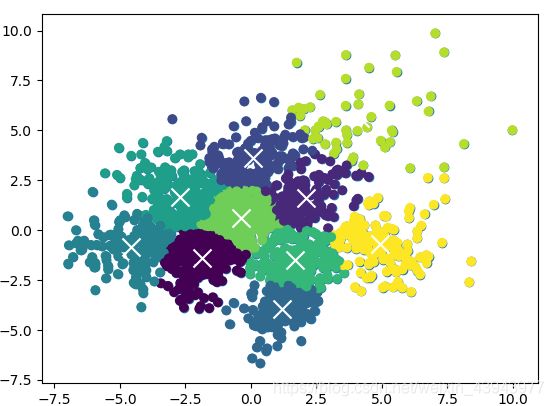
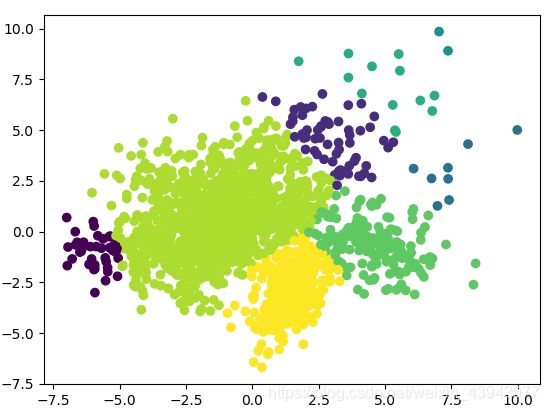
在通俗的理解中,聚类后的结果应该是不同类以不同的颜色来表明,所以在修改的时候我用不同颜色来表示不同的聚类点,最后再加上聚类中心,会有更加直观的结果:
plt.scatter(reduced_data[:, 0], reduced_data[:, 1],c=kmeans.labels_)
- 使用不同的方法对digits数据集聚类
有了前一部分的探索,使用其他的聚类方法处理起来就会相对轻松,下面我们分别来看这几种方法的聚类和评估结果:
- AffinityPropagation
使用AffinityPropagation的核心算法如下所示:
af = AffinityPropagation().fit(reduced_data)
result = af.labels_
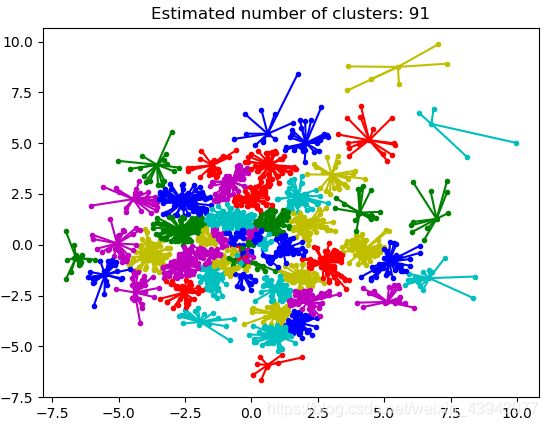
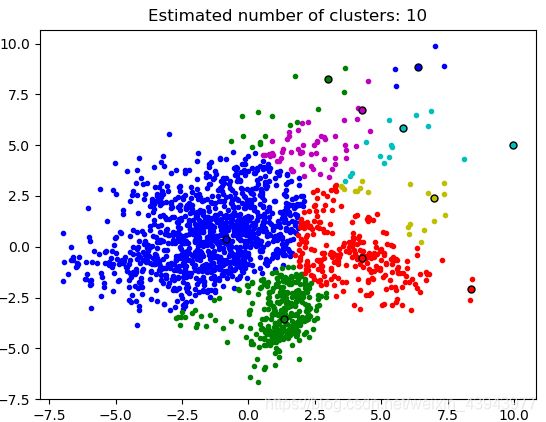
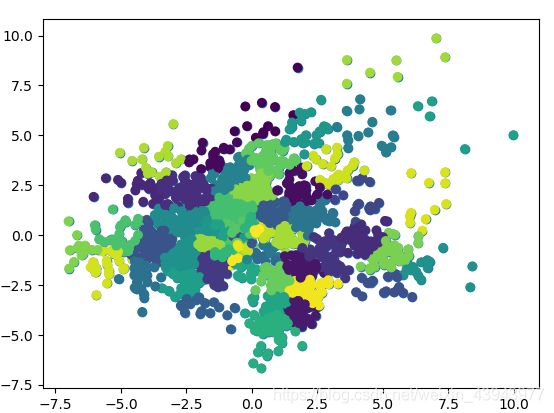
按照demo模型形式,绘制出来的效果如下:
(是不是很丑,分了90余类),按照我修改后的方式,效果稍微好点(只是相对好点):
- MeanShift
bandwidth = estimate_bandwidth(reduced_data, quantile=0.1)#经过测试,在quantile=0.1的情况下得到的结果是最好的
bench_k_means(MeanShift(bandwidth=bandwidth, bin_seeding=True),name="MeanShift",data=data)
meanshift = MeanShift(bandwidth=bandwidth, bin_seeding=True).fit(reduced_data)
init time nmi homo comp labelnum
MeanShift 2.72s 0.554 1.000 0.307 10
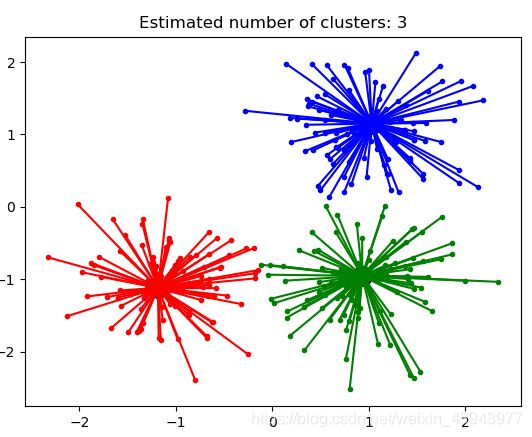
使用demo的效果本身就很好,如下:
- SpectralClustering
pca = PCA(n_components=n_digits).fit_transform(data)#要使用数据降维是因为高维情况在建图过程存在数据缺失bench_k_means(SpectralClustering(n_clusters=10),name="spectralcluster",data=pca)
init time nmi homo comp labelnum
spectralcluster 5.15s 0.598 0.449 0.796 10
这个聚类是没有聚类中心的。
- ward hierarchical clustering
ward = AgglomerativeClustering(n_clusters=10, linkage='ward')
ward.fit(data)
init time nmi homo comp
ward hierarchical clustering 0.36s 0.797 0.758 0.836
其他的聚类情况可视化效果都类似,这里不再一一可视化。只给出评估指标:
- AgglomerativeClustering
clustering = AgglomerativeClustering().fit(data)
- DBSCN
db = DBSCAN().fit(data)
result = db.labels_
init time nmi homo comp
DBSCAN 0.53s 0.375 0.000 1.000
- 对比
以下是上面各种方法的指标对比:
init time nmi homo comp
k-means++ 0.28s 0.626 0.602 0.650
random 0.22s 0.689 0.669 0.710
PCA-based 0.03s 0.681 0.667 0.695
AP 6.71s 0.655 0.932 0.460
MeanShift 2.72s 0.554 1.000 0.307
spectralcluster 5.15s 0.598 0.449 0.796
whc 0.36s 0.797 0.758 0.836
AC 0.21s 0.466 0.239 0.908
DBSCAN 0.53s 0.375 0.000 1.000
- 小结
各种方法看下来,还是感觉k-means算法是最经典的算法,尽管在种子选点的方式上存在随机性,但这个算法的逻辑和原理,对聚类的测定和迭代方法是它成为最经典,也是首选的聚类方法,在各个评价指标上都有一个相对较好的结果。其他方法各有优劣,如AP和sc的时间复杂性较高,也有些准确度上有较大的偏差,无法求得聚类中心等,但感谢各方的优秀工程师提供的这些聚类算法为我们提供了多种数据的聚类方式,成为sklearn的重要部分之一;
太多了,再往下写我hold不住了,就先到这里,其他的聚类等待看下一篇吧!
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from time import time
from sklearn import metrics
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.metrics import normalized_mutual_info_score
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import scale
from sklearn.cluster import KMeans, AffinityPropagation, estimate_bandwidth, MeanShift, SpectralClustering, \
AgglomerativeClustering, DBSCAN
#Loading digits data
np.random.seed(42)
digits = load_digits()
data = scale(digits.data)
n_samples, n_features = data.shape
n_digits = len(np.unique(digits.target))
labels = digits.target
sample_size = 300
print("n_digits: %d, \t n_samples %d, \t n_features %d"
% (n_digits, n_samples, n_features))
print(82 * '_')
print('init\t\ttime\tnmi\thomo\tcompl')
#Evaluation
def bench_k_means(estimator, name, data):
t0 = time()
estimator.fit(data)
print('%-9s\t%.2fs\t%.3f\t%.3f\t%.3f'
% (name, (time() - t0),
#metrics.normalized_mutual_info_score(labels, estimator.labels_),
metrics.v_measure_score(labels, estimator.labels_),
metrics.homogeneity_score(labels, estimator.labels_),
metrics.completeness_score(labels, estimator.labels_)))
#kmeans
bench_k_means(KMeans(init='k-means++', n_clusters=n_digits, n_init=10),name="k-means++", data=data)
bench_k_means(KMeans(init='random', n_clusters=n_digits, n_init=10),name="random", data=data)
pca = PCA(n_components=n_digits).fit(data)
bench_k_means(KMeans(init=pca.components_, n_clusters=n_digits, n_init=1),name="PCA-based",data=data)
#AffinityPropagation
bench_k_means(AffinityPropagation(),name="AffinityPropagation", data=data)
# MeanShift
bandwidth = estimate_bandwidth(data, quantile=0.1)
bench_k_means(MeanShift(bandwidth=bandwidth, bin_seeding=True),name="MeanShift",data=data)
# ward hierarchical clustering
bench_k_means(AgglomerativeClustering(n_clusters=10, linkage='ward'),name="ward hierarchical clustering",data=data)
# AgglomerativeClustering
bench_k_means(AgglomerativeClustering(),name="AgglomerativeClustering",data=data)
# DBSCN
bench_k_means(DBSCAN(),name="DBSCAN()",data=data)
print(82 * '_')
reduced_data = PCA(n_components=2).fit_transform(data)
# Visualize the results on PCA-reduced data way1
# example:meanshift
bandwidth = estimate_bandwidth(reduced_data, quantile=0.07)
meanshift = MeanShift(bandwidth=bandwidth, bin_seeding=True).fit(reduced_data)
result = meanshift.labels_
centroids = meanshift.cluster_centers_
labels_unique = np.unique(result)
n_clusters_ = len(labels_unique)
plt.figure(1)
plt.clf()
colors = cycle('bgrcmybgrcmybgrcmybgrcmy')
for k, col in zip(range(n_clusters_), colors):
my_members = result == k
cluster_center = centroids[k]
plt.plot(reduced_data[my_members, 0], reduced_data[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=5)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
# Visualize the results on PCA-reduced data way2
# example:kmeans
kmeans = KMeans(init='k-means++', n_clusters=n_digits, n_init=10)
kmeans.fit(reduced_data) # 对降维后的数据进行kmeans
result = kmeans.labels_
plt.figure(2)
plt.clf()
plt.scatter(reduced_data[:, 0], reduced_data[:, 1],c=result)
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='w', zorder=10)
plt.show()