数学建模----拟合的实现
一次作业展示
我用的是Python编写程序。也就 Scipy 里的 curve_fit指令
curve_fit指令是由一点小问题的。
我们小看一下具体的问题
- 引入相关包
from scipy.optimize import curve_fit
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rcParams["font.sans-serif"] = ["SimHei"]
matplotlib.rcParams["axes.unicode_minus"] = False- 定义需要你拟合的函数
def fun(t,a,b,c):
return a + b*t + c*t**2- 定义界限
#bounds
bounds = [[0,0,0],[1,2,3]]
#表示 amin,bmin,cmin ; amax,bmax,cmax- 设置参数并开始拟合
x = [0.01 * i for i in range(1000)]
y = [0.7+1.5*i+2.1*i**2 for i in x]
p_fit,pcov = curve_fit(fun,x,y,bounds=bounds)
a,b,c = p_fit.tolist()
print("a "+str(a))
print("b "+str(b))
print("c "+str(c))
>>>a 0.7000000000000016
>>>b 1.4999999999999993
>>>c 2.1- tips 实际工作的时候,你会发现,这个工作绝对没有我这里展示得这么简单。
- parameters
- 你会发现,虽然它有很多个参数,但非数学学院的孩子可能已经发现,这个恐怕是略有难度的(请上官网阅读)
- f
- xdata
- ydata
- bounds
- return
- popt
- 按照SSE最小的原则选出的最优参数
- pcov
- 协方差矩阵
- popt
- Raises
- ValueError
- xdata 或 ydata 中含有 Not a Number
- RuntimeError
- 最小二乘法跑不动啦
- OptimizeWarning
- 协方差矩阵无法估计得出
- ValueError
- parameters
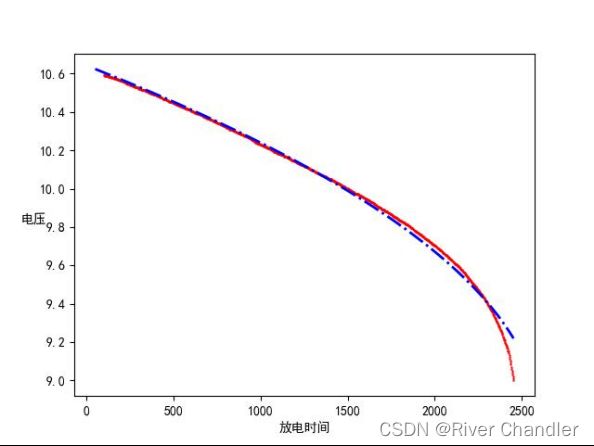
- 采样曲线
- 数据先期处理
-
前段数据明显有很大的偏差,是一个很不合理的数据。所以清洗掉前 50 个数据后我们得到图像,这个图像就合理多了。
-
- 我们最好使用一个指数函数来描述它的降落。但也许一个多项式函数也很有价值呢?所
- 参数
-
V0
10.999999999574499
a
-0.000498879687115049
b
-0.2948910057472579
c
0.00474997000539258
d
-8.960374326579795e-07
- 残差 SSE= 0.8664783171803022
-
import xlrd as xl
import matplotlib.pyplot as plt
import matplotlib
import math
from scipy.optimize import curve_fit
matplotlib.rcParams["font.sans-serif"] = ["SimHei"]
matplotlib.rcParams["axes.unicode_minus"] = False
data = xl.open_workbook("附件2 电池放电测试(30A)采样数据.xls")
work_sheet = data.sheets()[0]
all_rows = work_sheet.nrows
time,voltage = [0 for i in range(all_rows-1)],[0 for i in range(all_rows-1)]
for i in range(1,all_rows):
time[i-1] = work_sheet.cell_value(i,0)
voltage[i-1] = work_sheet.cell_value(i,1)
#plt.plot(time,voltage,label="电池放电")
#plt.xlabel("放电时间")
#plt.ylabel("电压",rotation=True)
#plt.legend()
#plt.savefig("电池放电原始记录,jpg")
#plt.cla()
#plt.plot(time[5:],voltage[5:],label="电池放电")
#plt.xlabel("放电时间")
#plt.ylabel("电压",rotation=True)
#plt.legend()
#plt.savefig("电池放电清洗后记录,jpg")
start = 50
time = time[start:]
voltage = voltage[start:]
plt.scatter(time,voltage,marker="o",c="red",s=0.5)
def fun(t,v0,a,b,c,d):
#v0*math.e**(a*t)+
#+(b*t+c*t**2+d*t**3)
#return v0*math.e**(a*t)+(b+c*t+d*t**2)
return v0*math.e**(a*t)+(b+c*t+d*t**2)
p_fit,pcov = curve_fit(fun,time,voltage,bounds=[[9,-2,-2,-2,-2],[11,2,2,2,2]])
v0,a,b,c,d = p_fit.tolist()
time0 = [i for i in range(start,int(time[-1]))]
plt.plot(time0,[fun(i,v0,a,b,c,d) for i in time0],linestyle="-.",c="b",linewidth=2)
SSE = sum([(fun(time[i],v0,a,b,c,d)-voltage[i])**2 for i in range(len(time))])
plt.xlabel("放电时间")
plt.ylabel("电压",rotation=True)
plt.savefig("电池放电拟合图.jpg")
plt.show()
print(SSE)-
为了缩减误差,我们将每个电压值减去9,做同样的操作后,得到
- 参数
-
V0
1.5999999999996954
a
-0.0011712982921128377
b
0.10761472318925852
c
0.0010752299243068316
d
-4.353127243058634e-07
- 残差 SSE= 1.0248705943495118
-
import xlrd as xl
import matplotlib.pyplot as plt
import matplotlib
import math
from scipy.optimize import curve_fit
matplotlib.rcParams["font.sans-serif"] = ["SimHei"]
matplotlib.rcParams["axes.unicode_minus"] = False
data = xl.open_workbook("附件2 电池放电测试(30A)采样数据.xls")
work_sheet = data.sheets()[0]
all_rows = work_sheet.nrows
time,voltage = [0 for i in range(all_rows-1)],[0 for i in range(all_rows-1)]
for i in range(1,all_rows):
time[i-1] = work_sheet.cell_value(i,0)
voltage[i-1] = work_sheet.cell_value(i,1)
start = 50
time = time[start:]
voltage = voltage[start:]
voltage = [i-9 for i in voltage]
plt.scatter(time,voltage,marker="o",c="red",s=0.5)
def fun(t,v0,a,b,c,d):
#v0*math.e**(a*t)+
#+(b*t+c*t**2+d*t**3)
#return v0*math.e**(a*t)+(b+c*t+d*t**2)
return v0*math.e**(a*t)+(b+c*t+d*t**2)
p_fit,pcov = curve_fit(fun,time,voltage,bounds=[[1.4,-10,-10,-10,-10],[1.6,10,10,10,10]])
v0,a,b,c,d = p_fit.tolist()
time0 = [i for i in range(start,int(time[-1]))]
plt.plot(time0,[fun(i,v0,a,b,c,d) for i in time0],linestyle="-.",c="b",linewidth=2)
SSE = sum([(fun(time[i],v0,a,b,c,d)-voltage[i])**2 for i in range(len(time))])
plt.xlabel("放电时间")
plt.ylabel("电压",rotation=True)
plt.savefig("电池放电拟合图.jpg")
plt.show()
print(SSE)-
SSE变化不大,还行,说得过去。
其实这个问题还可以用更高级的方法解决。函数的主体部分一定是一个指数函数。至于误差的话,可以用支持向量机估计。
但是,最重要的问题是,电池电压的变化是有一定科学函数关系的。不太可能是随意给一个函数的。
我们查阅文献。
得到一个更好的方程
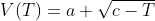
| a |
8.775331053692842 |
| b |
0.03661353006471206 |
| c |
2600.000378465227 |
| SSE |
0.9081344248801957 |
import xlrd as xl
import matplotlib.pyplot as plt
import matplotlib
import math
from scipy.optimize import curve_fit
matplotlib.rcParams["font.sans-serif"] = ["SimHei"]
matplotlib.rcParams["axes.unicode_minus"] = False
data = xl.open_workbook("附件2 电池放电测试(30A)采样数据.xls")
work_sheet = data.sheets()[0]
all_rows = work_sheet.nrows
time,voltage = [0 for i in range(all_rows-1)],[0 for i in range(all_rows-1)]
for i in range(1,all_rows):
time[i-1] = work_sheet.cell_value(i,0)
voltage[i-1] = work_sheet.cell_value(i,1)
start = 50
time = time[start:]
voltage = voltage[start:]
plt.scatter(time,voltage,marker="o",c="red",s=0.5)
def fun(t,v0,a,b,c,d):
return a+b*(c-t)**0.5
p_fit,pcov = curve_fit(fun,time,voltage,bounds=[[9,0,0,2600,0],\
[11,10,10,4600,10]])
v0,a,b,c,d = p_fit.tolist()
time0 = [i for i in range(start,int(time[-1]))]
plt.plot(time0,[fun(i,v0,a,b,c,d) for i in time0],linestyle="-.",c="b",linewidth=2)
SSE = sum([(fun(time[i],v0,a,b,c,d)-voltage[i])**2 for i in range(len(time))])
plt.xlabel("放电时间")
plt.ylabel("电压",rotation=True)
plt.savefig("电池放电拟合图.jpg")
plt.show()
print(SSE)
-
这样的残差平方和事实上已经很小了,只是你要明白一点就是,电池的结构决定了电池的放电规律不太可能用一个初等函数来表示。更有可能是一个更复杂的方程,这是由电池决定的,而不是有观测值决定的。
电池的放电规律与一般得分类问题不同,它是很难得到检验的。我们不能通过选取一个阶段的放电,将它与预测值比较来反映模型的准确性。即使考虑最简单的RLC电路,方程的解也不是严格得如我们的预测方程所示。
我们的拟合最多能够给出电池的放电结束时间,而且不一定准确。我们的拟合使函数尽可能得符合曲线而不是趋近物理事实,这是不合理的。或者对于同样的一块电池,预估放电时间与电压的关系。
研究物理过程不能只从现象观察,应该去研讨物理规律。当然,更加好的一个办法呢,还是使用分段函数来做它,在放电的最初阶段和最末阶段,电压的下降速率远远大于中间阶段,在物理过程不明晰的情况下,还是分段研究比较合理。
-
如果从软件使用的角度来看,我们初始值的选取是十分重要的。Science Python的curve_fit和Mathematica 的智能程度远远低于matlab或者其他软件。即使是使用Matlab,初始值的选取也能大大得减少运算时间。对于初始值怎么选呢?慢慢调参吧。。