机器学习模型性能度量详解 【Python机器学习系列(十六)】
机器学习模型性能度量 【Python机器学习系列(十六)】
文章目录
- 1. 错误率 与 精度
- 2. 查准率 查全率 与 F1
-
- 2.1 TP、FP、FN、 TN
- 2.2 查准率 与 查全率
- 2.3 P-R 图 与 平衡点
- 2.4 F1
- 2.5 宏查准率 & 宏查全率 & 宏F1
- 2.6 微查准率 & 微查全率 & 微F1
- 3. ROC与AUC
- 4. python计算ROC,AUC
-
- 4.1 二分类情形
- 4.2 多分类情形与macro-AUC
性能度量,即对机器学习模型的泛化能力进行评估的过程。要进行性能度量,首先需要认识并掌握多种性能度量指标。
机器学习的任务可以分为回归任务和分类任务。回归任务中常用的性能度量指标是均方误差。这个较为基础,这里不多赘述。这里主要关注分类任务的性能度量指标。
1. 错误率 与 精度
错误率 与 精度 是一对相反的指标。
错误率即分类错误的样本占总样本数的比例。
精度即分类正确的样本占总样本数的比例。
这两个指标的和为1。
2. 查准率 查全率 与 F1
2.1 TP、FP、FN、 TN
首先认识四组概念:
| 名称 | 简写 | 通俗描述 |
|---|---|---|
| 真正例 | TP | 预测结果是该标签,实际是该标签的样例个数 |
| 假正例 | FP | 预测结果是该标签,实际不是该标签的样例个数 |
| 假反例 | FN | 预测结果不是该标签,实际是该标签的样例个数 |
| 真反例 | TN | 预测结果不是该标签,实际不是该标签的样例个数 |
则这四组指标满足TP+FP+FN+TN=样例总数。
2.2 查准率 与 查全率
查准率和查全率,也是一对矛盾的变量。其针对的是分类问题的某一个类别。对一个机器学习模型某一次的预测结果中,对于不同的分类类别,可以有多个不同的查准率和查全率,而不是唯一的。
查准率(precision):
P = P= P= T P T P + F P \frac{TP}{TP+FP} TP+FPTP
即:预测结果是某标签的样例中,实际真的是该标签的样例所占的比例。
查全率(recall):
R = R= R= T P T P + F N \frac{TP}{TP+FN} TP+FNTP
即:实际是某标签的样例中,预测结果是该标签的样例所占的比例。
2.3 P-R 图 与 平衡点
P-R图
一般来讲,查准率高的时候查全率会偏低;查全率高的时候查准率会偏低。
对于某个类别(如类别A),以该类别为正例,则对于一个测试集,最后可以得到测试集中每个样本预测为正例的概率,把这些样本按照概率从大到小的顺序进行排列。然后把这些样本全部预测为正例逐个进行预测(累计)。即可得到“P-R曲线”。
P-R曲线示例如下图所示:
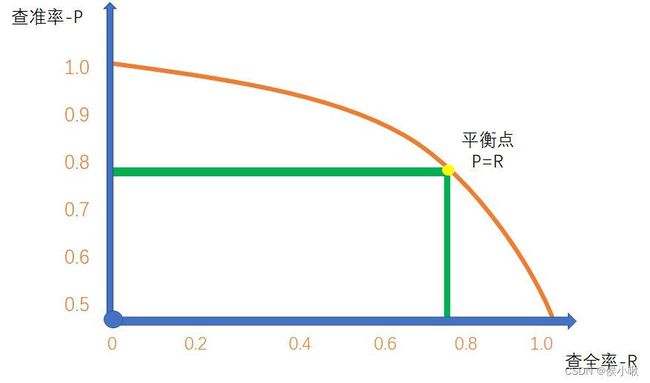
如何理解这条线呢?
从左上角的查准率为1,查全率为0的点开始看起,此时可以理解为预测的样本数量为0,也就是说,将0个样本都预测为正例,此时的查准率视为1,而因为实际为正例的样本没有一个被预测为正例,所以查全率为0。随着曲线上的点向右移动,也就是把样本点按照判断为正例的概率大小,从大大小逐个添加的过程,随着正例被预测到的越来越多,查全率在不断提高。但是这个过程中以及即使为正例概率较大的样本,也不能保证其100%是正例。所以查全率在前期不会是一条水平的直线。而在后期,也会根据要求把是正例概率较低的样本预测为正例,所以曲线会按照如图所示的走势。且最查全率趋于1时,终查准率通常不会趋于0,而是趋于一个大于0的数字,即全部预测为正例时,预测正确的样本所占总样本的比例。
通常,如果一个机器学习模型的P-R曲线A被另一个模型的P-R曲线B完全包住,则可以断言B优于A。
如果A与B较差,则很难断言哪个更好。
此时可以用 平衡点(Break-Event Point, BEP) 来衡量。平衡点,是P-R图中查准率等于查全率时的取值。
2.4 F1
相比BEP,F1是更为常用的度量指标。
F1是基于查准率和查全率的调和平均。
公式为:
F 1 = F1= F1= 2 × P × R P + R = 2 × T P 样例总数 + T P − T N \frac{2×P×R}{P+R}=\frac{2×TP}{样例总数+TP-TN} P+R2×P×R=样例总数+TP−TN2×TP
这一点有一点逻辑需要理清楚,不要跟平衡点弄混淆。平衡点与F1的确定,并不是仅仅基于一个机器学习模型就足够的,都需要一组用于测试的样本数据集,且需要将某类别为正例,才可对应一个平衡点与一个F1。
对于不同的样本数据集,或选择不同的类别作为正例,对应着多种不同结果,而非唯一的。
研究平衡点与P-R曲线时,强行把样本数据集中的所有样本都判断为正例,且根据排序有序推进得到的是构成一条曲线的多个查准率与查全率。而平衡点选择的是查准率与查全率 相等 时候的一个数值。
而F1对应的查准率P与查全率R,与P-R图是毫无关联的。其对应的查准率与查全率,也即对于某个测试样本数据集,以某个类别为正例时的唯一查准率与查全率。不要混淆。
此外, F 1 F1 F1度量的一般形式 F β F_\beta Fβ,可以表达出对查准率和查全率的偏好:
F β = F_\beta= Fβ= ( 1 + β 2 ) × P × R ( β 2 × P ) + R \frac{(1+\beta^2)×P×R}{(\beta^2×P)+R} (β2×P)+R(1+β2)×P×R
β > 0 \beta>0 β>0度量的是查全率对查准率的重要性。
当 β = 1 \beta=1 β=1时,即F1;
当 β > 1 \beta>1 β>1时,查全率有更大的影响;
当 β < 1 \beta<1 β<1时,查准率有更大的影响。
2.5 宏查准率 & 宏查全率 & 宏F1
很多时候,可以得到多个混淆矩阵。如进行多次训练或测试,或有多个数据集,或者执行多分类任务。这样情况下,为了考察全局性能, 这里引入 宏查准率(macro-P)、宏查全率(macro-R)、 宏F1(macro-F1)三个指标。
宏查准率,则是将多个查准率分求均值。
宏查全率,则是将多个查全率求均值。
宏F1,则是使用宏查准率macro-P和宏查全率macro-R代替原来的P和R计算出的F1。
2.6 微查准率 & 微查全率 & 微F1
微查准率、微查全率、微F1,则是在计算多个TP、FP、TN、FN的时候,将其求均值。再使用得到的均值来计算出的即是微查准率(micro-P) 、微查全率(micro-R)、 微F1(micro-F1)。
3. ROC与AUC
ROC的全称是受试者工作特征(Receiver Operatng Characteristic)曲线。
其原理思想与P-R曲线相似,只是横纵轴的指标不相同。
对于一个机器学习模型,一组测试数据集,指定一个类别为正例,然后根据预测结果中每个样本是正例的概率,对测试数据集中的每个样本进行从大到小排序。然后依次逐个把每个样本都判断为正例,这样随着判断的样本越来越多,我们就可以得到一系列真正例率(True Positive Rate, TPR)和假正例率(False Positive Rate, FPR)。
真正例率的计算公式为:
T P R = TPR= TPR= T P T P + F N \frac{TP}{TP+FN} TP+FNTP
表示实际为正例的样本中,成功预测为正例的样本的比例。(相当于上边P-R图中的查全率)
假正例率的计算公式为:
F P R = FPR= FPR= F P T N + F P \frac{FP}{TN+FP} TN+FPFP
表示实际为不是正例的样本中,预测为正例的样本的比例。
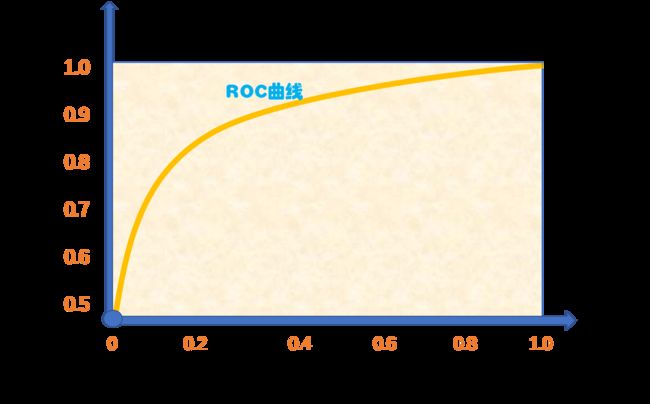
分别以假正利率和真正例率为横、纵轴,得到的图线即为ROC曲线,示例如图所示:
ROC曲线下方包围的面积,即为AUC(Area Under ROC Curve)。
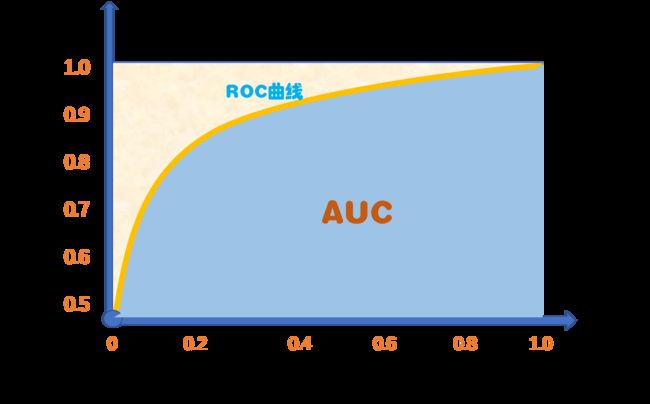
当然,这里的ROC曲线只是理想状态下的。现实中往往测试样本会比较少,绘制图形时只能用几个有限的坐标对,常常得不到这么完美的曲线,而是得到如下图所示的ROC曲线和AUC:
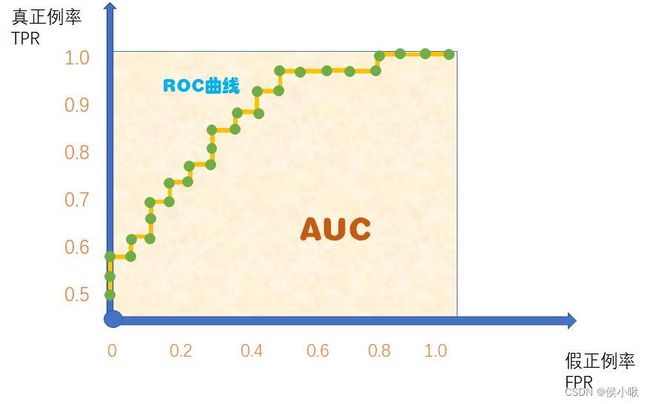
4. python计算ROC,AUC
4.1 二分类情形
以二分类为例,计算ROC和AUC的代码如下。
from sklearn.metrics import auc,roc_curve,roc_auc_score
# 准备一组标签合数和一组概率数据
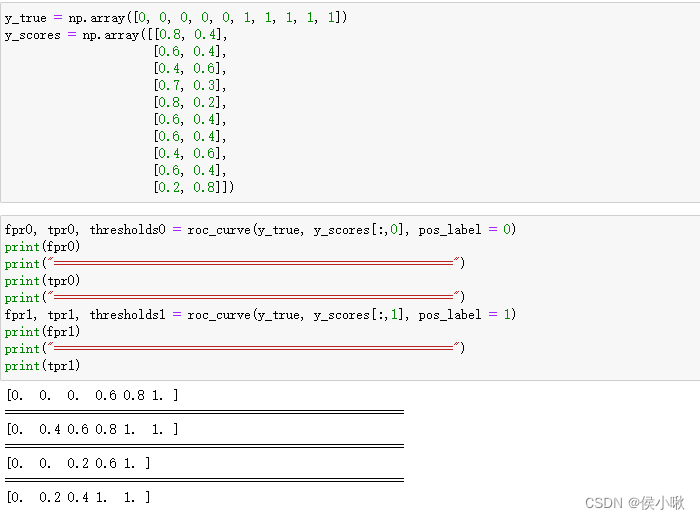
y_true = np.array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
y_scores = np.array([[0.8, 0.4],
[0.6, 0.4],
[0.4, 0.6],
[0.7, 0.3],
[0.8, 0.2],
[0.6, 0.4],
[0.6, 0.4],
[0.4, 0.6],
[0.6, 0.4],
[0.2, 0.8]])
# 以标签值为0为正例,求假正例率和真正利率
fpr0, tpr0, thresholds0 = roc_curve(y_true, y_scores[:,0], pos_label = 0)
print(fpr0)
print("=========================================================")
print(tpr0)
print("=========================================================")
# 以标签值为1为正例,求假正例率和真正利率
fpr1, tpr1, thresholds1 = roc_curve(y_true, y_scores[:,1], pos_label = 1)
print(fpr1)
print("=========================================================")
print(tpr1)
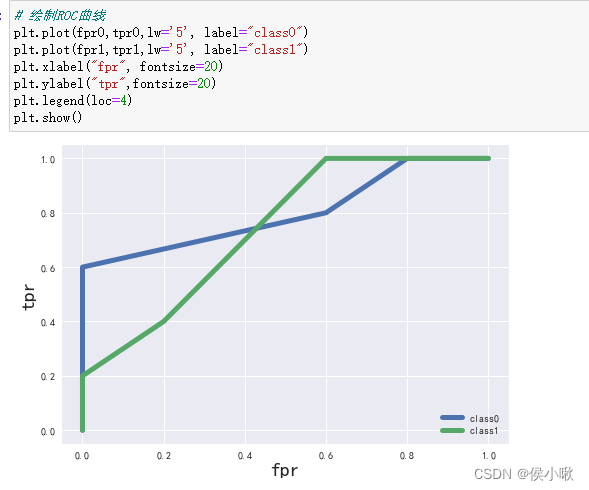
然后绘制roc曲线。
# 绘制ROC曲线
plt.plot(fpr0,tpr0,lw='5', label="class0")
plt.plot(fpr1,tpr1,lw='5', label="class1")
plt.xlabel("fpr", fontsize=20)
plt.ylabel("tpr",fontsize=20)
plt.legend(loc=4)
plt.show()
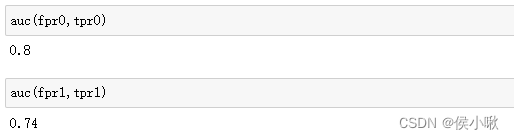
分别计算0为正例 和 1为正例时的AUC值:
auc(fpr0,tpr0)
auc(fpr1,tpr1)
也可以使用roc_auc_score()方法,在二分类的情形下,只能求出将标签值为1视为正例时的AUC值,该方法计算AUC值不需要求真正例率和假正例率,只需要传入真实的标签,以及预测判断每个样本为正例的概率。具体代码如下:
roc_auc_score(y_true, y_scores[:,1])

(如果传入y_scores[:,0],则得到的是错误的结果,不会得到上边的0.8)。
4.2 多分类情形与macro-AUC
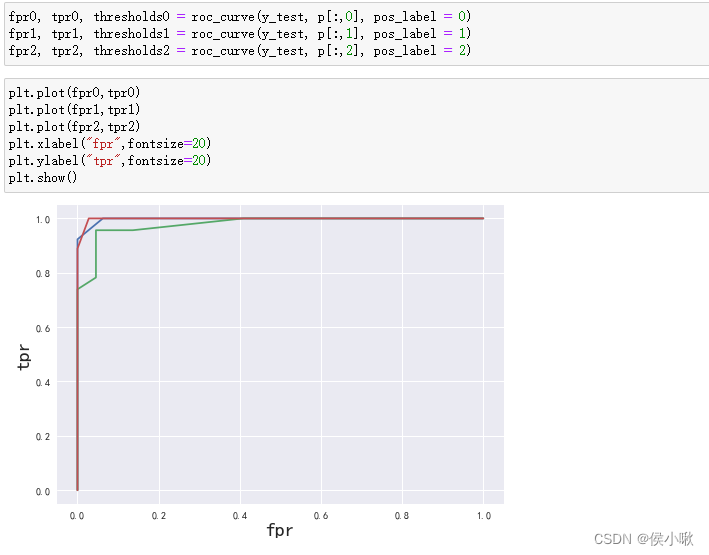
以三分类为例,标签有0,1,2三个,测试集的真实标签为y_test,预测概率为p,如下图所示:
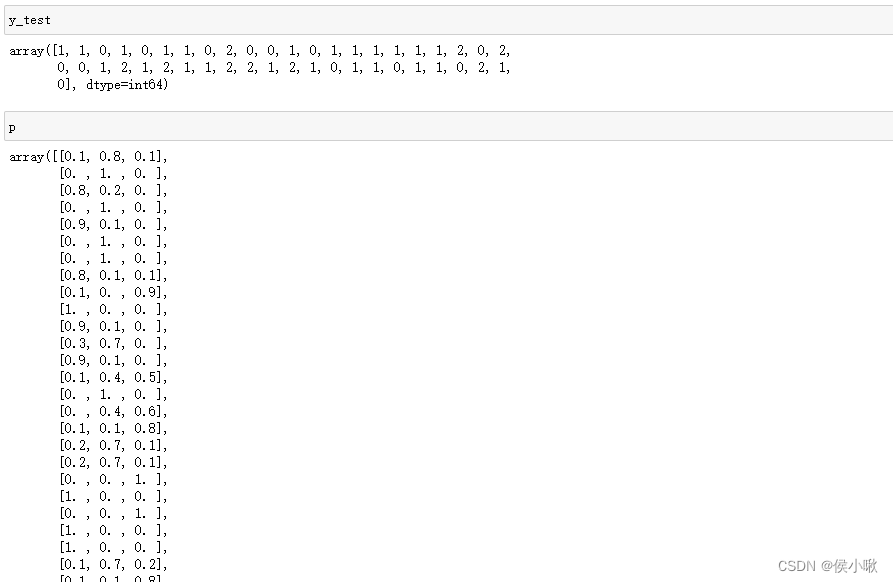
则绘制ROC曲线:
fpr0, tpr0, thresholds0 = roc_curve(y_test, p[:,0], pos_label = 0)
fpr1, tpr1, thresholds1 = roc_curve(y_test, p[:,1], pos_label = 1)
fpr2, tpr2, thresholds2 = roc_curve(y_test, p[:,2], pos_label = 2)
plt.plot(fpr0,tpr0)
plt.plot(fpr1,tpr1)
plt.plot(fpr2,tpr2)
plt.xlabel("fpr",fontsize=20)
plt.ylabel("tpr",fontsize=20)
plt.show()
分别以0,1,2为正例,计算出的AUC值为:
auc0 = auc(fpr0, tpr0)
auc1 = auc(fpr1, tpr1)
auc2 = auc(fpr2, tpr2)
print(auc0,auc1,auc2)
roc_auc_score()方法,在多分类中,与二分类有所不同。可以通过roc_auc_score()方法来计算AUC的均值,从而评估模型的整体性能。
sklearn.metrics.roc_auc_score(y_true, y_score, average=’macro’, sample_weight=None, max_fpr=None)
roc_auc_score(y_test,p,multi_class='ovr')
本次分享就到这里,小啾感谢您的关注与支持!
꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ
本专栏更多好文欢迎点击下方连接:
1.初识机器学习前导内容_你需要知道的基本概念罗列_以PY为工具 【Python机器学习系列(一)】
2.sklearn库数据标准预处理合集_【Python机器学习系列(二)】
3.K_近邻算法_分类Ionosphere电离层数据【python机器学习系列(三)】
4.python机器学习 一元线性回归 梯度下降法的实现 【Python机器学习系列(四)】
5.sklearn实现一元线性回归 【Python机器学习系列(五)】
6.多元线性回归_梯度下降法实现【Python机器学习系列(六)】
7.sklearn实现多元线性回归 【Python机器学习系列(七)】
8.sklearn实现多项式线性回归_一元/多元 【Python机器学习系列(八)】
9.逻辑回归原理梳理_以python为工具 【Python机器学习系列(九)】
10.sklearn实现逻辑回归_以python为工具【Python机器学习系列(十)】
11.决策树专题_以python为工具【Python机器学习系列(十一)】
12.文本特征提取专题_以python为工具【Python机器学习系列(十二)】
13.朴素贝叶斯分类器_以python为工具【Python机器学习系列(十三)】
14.SVM 支持向量机算法(Support Vector Machine )【Python机器学习系列(十四)】
15.PCA主成分分析算法专题【Python机器学习系列(十五)】