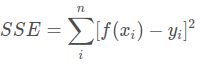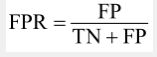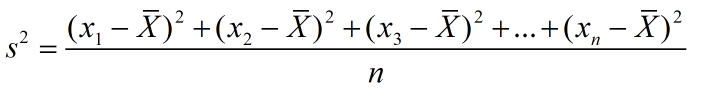机器学习笔记1——机器学习的分类、性能度量以及特征工程
一、分类
1.1 按任务类型
回归模型
分类模型
结构化学习模型
1.2 按学习理论
监督学习:训练样本带有标签
半监督学习:训练样本部分有标签
无监督学习:训练样本无标签,例如聚类算法
强化学习:智能体通过环境进行交互获得的奖赏来指导自己的行为,最终目标是使智能体获得最大的奖赏
二、性能度量
2.1 回归问题
回归问题的标记yi一般都是实值,不能通过是否相等进行评估。一般是通过衡量预测值f(xi)和真实值yi之间的距离。
2.1.1 均方误差(MSE)
mean square error
2.1.2 均方根误差(RMSE)
root mean square error,观测值与真值偏差的平方和与观测次数m比值的平方根,用来衡量观测值同真值之间的偏差。
2.1.3 和方误差(SSE)
2.1.4 平均绝对误差(MAE)
mean absolute error,直接计算模型输出与真实值之间的平均绝对误差
引入百分比之后,可以有效避免因为样本的绝对数值引起的评估不恰当问题。比如对于房价的预测,数值一般为几万/平,而对于人身高的预测,一般为1.x米。直接使用MAPE,可能会碰到如果遇到除数为0的情况,这个指标就没法计算
2.1.5 平均绝对百分比误差(MAPE)
mean absolute percentage error,不仅考虑预测值与真实值误差,还考虑了误差与真实值之间的比例。

2.1.6 平均平方百分比误差(MASE)
mean square percentage error
2.1.7 决定系数R2
SSE:表示真实值与预测值之间误差的平方和
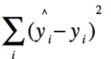
SST:表示真实值与均值之间误差的平方和
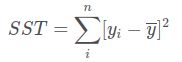
SST = SSE + SSR
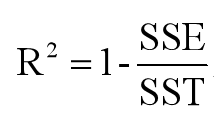
- R2=0:表示模型拟合效果差
- R2=1:表示模型拟合效果非常好,无错误
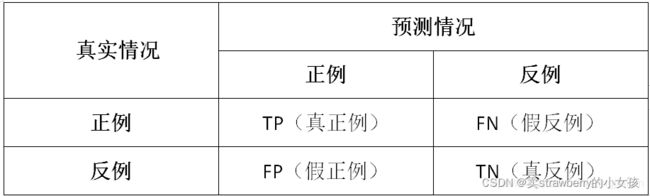
2.2 分类问题
TP:正样本被模型预测为正样本(真正例,true positive)
FN:正样本被模型预测为负样本(假反例,false negative)
FP:负样本被模型预测为正样本(假正例,false positive)
TN:负样本被模型预测为负样本(真反例,true negative)
2.2.1 精确率、查准率(Precision)
预测为真的样本中实际是真的的概率,适用于对准确率要求高的应用:网页检索与推荐
![]()
2.2.2 召回率、查全率(Recall)
所有实际为真的样本被预测为真的的概率,适用于检测信贷风险、逃犯信息
![]()
2.2.3 F1
精确率与召回率相互矛盾,所有找一个平衡点,F1是精确率与召回率的调和平均值
1/(F1) = 1/2 * (1/ P) + 1/2 * (1/ R)
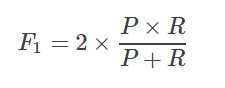
2.2.4 真正例率(TPR)
实际为真的样本被判断为正例,为召回率
2.2.4 假正例率(FPR)
2.2.5 错误率和准确率
错误率和准确率是最常用的分类问题性能度量的指标
错误率:统计分类器预测出来的结果与真实结果不相同的个数,然后除以总的样例的个数n。
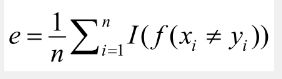
准确率acc=1-e:预测结果=真实结果相同的个数 / 总的样例的个数n
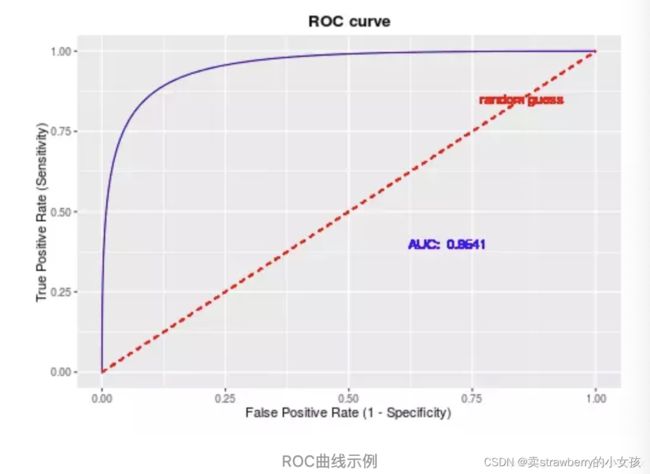
2.2.6 AUC、ROC曲线
对于0、1分类问题,一些分类器得到的结果不是0,1,如神经网络为0.5,0.6…,需要一个阈值cutoff,小于cutoff的归为0类,大于等于阈值的归为1类。
ROC曲线:
横坐标为FPR,纵坐标为TPR,主要意义是方便观察阈值对学习器的泛化性能影响
AUC:
1、为ROC曲线所覆盖的区域面积(曲线下方面积即为AUC值),AUC越大,表示该方法越有利于区分两种类别
2、是一个概率值,当随机挑选一个正样本和负样本,当前的分类算法根据计算得到的Score值将正样本排在负样本前边的概率
#方法一
from sklearn.metrics import roc_curve, auc
###得到roc数据
# 数据准备
import numpy as np
from sklearn import metrics
y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
# roc_curve的输入为
# y: 样本标签
# scores: 模型对样本属于正例的概率输出
# pos_label: 标记为正例的标签,本例中标记为2的即为正例
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
auc = metrics.auc(fpr, tpr)
###绘制ROC曲线
import matplotlib.pyplot as plt
plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
三、特征工程
数据和特征决定了机器学习的上限,二模型和算法只是逼近这个上限。
3.1 数据预处理
3.1.1 无量纲化
解决数据的量纲不同的问题,使不同的数据转换到同一规格,常见的方法:
1. 标准化
适用于服从正态分布的数据,标准化后,转换成标准正态分布。
在样本足够多的情况下,往往直接使用标准化对数据进行无量纲化预处理。
如果不进行数据标准化,有些特征(值很大)会对损失函数影响更大,使得值比较小的特征重要性减低,因此数据标准化可以使得每个特征的重要性更加均衡,公式为:
![]()
方差:
①概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度;②统计中的方差(样本方差)是每个样本值与全体样本均值之差的平方值的平均数,代表每个变量与总体均值间的离散程度。
概率论:
离散型随机变量:
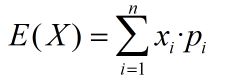
连续型随机变量:
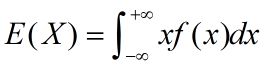
方差
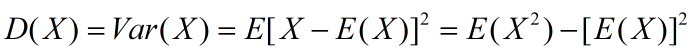
统计学:
代码:
from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
# 法一
scaler = StandardScaler()
# fit 用于计算训练数据的均值和方差,StandardScaler().fit(data) 这一步可以得到scaler,scaler里面存的有计算出来的均值和方差
scaler.fit(data)
StandardScaler(copy=True, with_mean=True, with_std=True)
# print(scaler.mean_) # [ 0.5 0.5]
print(scaler.transform(data))
# [[-1. -1.]
# [-1. -1.]
# [ 1. 1.]
# [ 1. 1.]]
# 法二
# fit_transform()不仅计算训练数据的均值和方差,还会基于计算出来的均值和方差来转换训练数据,从而把数据转换成标准的正态分布
print(StandardScaler().fit_transform(data))
2.区间缩放法 / 归一化:
适用于数据量较小的工程
利用了边界值信息,将特征的取值区间缩放到某个特定的范围,例如[0,1],利用两个最值进行缩放。

具体计算:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
axis=0表示是在某一列中查找最大值/最小值,对于以下a矩阵中的2(第一行第二列元素),X.min(axis=0)是指第二列中的最小值2,X.max(axis=0)是指第二列中的最大值18
max,min分别是归一化范围的最大最小值
2–>-1 计算过程:(2 - 2) / (18 - 2) * (1 - (-1)) + (-1)
代码实现:
from sklearn.preprocessing import MinMaxScaler
import numpy as np
a = np.asarray([[-1, 2], [-0.5, 6], [0, 10], [1, 18]])
print(a)
scaler = MinMaxScaler(feature_range=(-1, 1)) # 归一化范围(-1,1)
b = scaler.fit_transform(a)
print(b)
# 模型输入数据必须是二维数据
3.1.2 哑编码与独热编码
如果某一列数据是一些特征,无法将这种信息应用到回归或者分类里的时候,使用:
独热码/独热编码(one-hot code)
一位有效编码,直观来说就是有多少个状态就有多少比特,而且只有一个比特为1,其他全为0的一种码制。例如国家这个特征有中国、美国、德国、法国四种可能的取值,那么独热码会用一个四维的特征向量表示该特征,每个维度对应一个国家,也叫状态位,独热码保证四个状态位有一个位置为1,其余是0。
代码:
from sklearn.preprocessing import OneHotEncoder
import numpy as np
data = np.array([[0], [1], [2]])
enc = OneHotEncoder(sparse=False)
data = enc.fit_transform(data)
print(data)
哑编码
任意的将一个状态位去除,n-1个状态位就足够反应n个类别的信息,当n-1个状态都是0时,剩下的那1个就是1。
3.1.3 缺失值补充
常用方法:均值、就近补齐、K最近距离填充等方法
如果缺失值过多,可以直接舍弃该列特征,否则会带来较大的噪声,从而对结果造成不良影响。如果缺失值较少(少于10%),可以考虑对缺失值进行填充。常见填充策略:
1)用一个异常值填充并将缺失值作为一个特征处理
2)用均值或条件均值填充,如果数据不平衡,使用条件均值。条件均值:与缺失值所属标签相同的所有数据的均值
3)用相邻数填充
4)利用差值算法
5)数据拟合:将缺失值作为一个预测问题来处理
数据集来源于 天池精准医疗大赛——人工智能辅助糖尿病遗传风险预测。该数据集共有1000条数据,特征共83维,加上id和label共85列,每维特征缺失数量范围为0~911。为了简单比较各种填充方法的效果,我们选取最简单的二分类模型(逻辑回归),选取F1 score作为评测指标
import pandas as pd
from sklearn.model_selection import train_test_split
train_data = pd.read_csv('train_data.csv', encoding='gbk') # 读取数据集
filter_feature = ['id', 'label'] # 过滤无用的维度
features = []
for x in train_data.columns: # 取特征
if x not in filter_feature:
features.append(x)
train_data_x = train_data[features]
train_data_y = train_data['label']
X_train, X_test, y_train, y_test = train_test_split(train_data_x, train_data_y, random_state=1) # 划分训练集、测试集
# 填充异常值
train_data.fillna(0, inplace=True) # 填充 0
# 填充均值
train_data.fillna(train_data.mean(), inplace=True)
# 填充相邻数
train_data.fillna(method='pad', inplace=True) # 填充前一条数据的值,但是前一条也不一定有值
train_data.fillna(0, inplace=True)
train_data.fillna(method='bfill', inplace=True) # 填充后一条数据的值,但是后一条也不一定有值
train_data.fillna(0, inplace=True)
3.2 特征选择
特征选择非常关键,选入大量特征不仅降低模型效果,还会耗费计算时间。漏选的特征也会影响最终模型效果。
3.2.1 方差选择法
某列特征数值变化一直平缓,说明该特征对结果的影响小,可计算各个特征的方差,选择方差大于自设阈值的特征
3.2.2 相关系数,统计检验
常用的,对于连续变量:pearson相关系数,离散变量:卡方检验
3.2.3 互信息法
3.2.4 基于机器学习的特征选择法
主要针对特征和响应变量建立预测模型,如:基于树的方法(决策树、随机森林、GBDT)等。
3.3 特征降维
如果特征矩阵过大,会导致训练时间过长,需要降低特征矩阵维度。降维有利于节省存储空间、加快计算速度、避免模型拟合。
降维:保留重要特征,减少数据特征的维度。特征重要性取决于特征能表达多少数据集的信息。
3.3.1 主成分分析法(PCA)
通过析取主成分显出的最大的个别差异,发现更便于人类理解的特征。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。如何找到让样本间距最大的轴,一般使用方差来定义样本之间的间距。
PCA
是一个将数据变换到一个新的坐标系统中的线性变换,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(称为第二主成分)上…,主要是为了让映射后的向量具有最大的不相关性。
主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
追求在降维后最大化的保持数据的内在信息,并通过衡量在投影方向上的数据方差大小来衡量该方向的重要性。
这位博主有详解:博客链接
3.3.2 线性判别分析法(LDA)
LDA是一种有监督的降维方法,主要是将高维的模式样本投影到最佳鉴别的空间,目的是保证同类的数据点尽可能地接近而不同类别的数据点尽可能地分开。
LDA与PCA的区别:
- LDA是有监督的降维方法,PCA是无监督的
- LDA降维最多降到类别数k-1的维数,PCA没有限制
- LDA选择分类性能最好的投影方向,PCA选择样本点投影具有最大方差的投影方向
PCA是为了让映射后的样本点发散性最大,LDA是为了映射后的样本分类性能更好
3.3.3 局部性嵌入(LLE)
该算法认为每个数据点都可以由邻近点的线性加权组合构造得到。
3.4 特征构造
针对具体的项目属性、数据特点来构造可能的重要特征。
参考《人工智能程序员面试笔试宝典》猿媛之家,凌峰