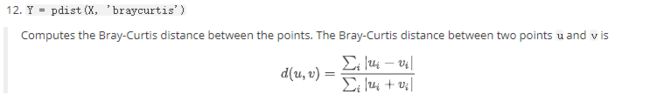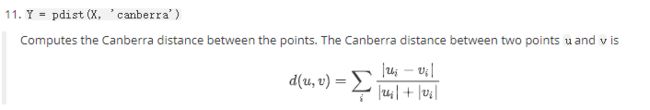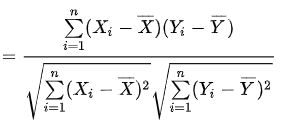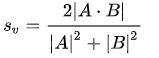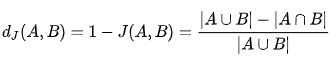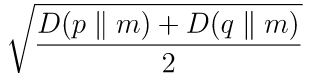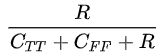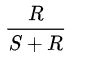机器学习领域几种距离度量方法metric详解

对scipy.spatial.distance.pdist(X, metric='euclidean', *args, **kwargs)中metric的介绍.

【常用的已标红】

1.braycurtis

Bray-Curtis 相异度（Bray-Curtis dissimilarity）是生态学中用来衡量不同样地物种组成差异的测度。其计算基于样本中不同物种组成的数量特征（多度，盖度，重要值等）。

布雷-柯蒂斯相异度介于0和1之间，0意味着两个调查样地的物种组成完全相同，而1则表示两个调查样地的物种组成完全不同。布雷-柯蒂斯相异度经常被误认为是一种距离测度（"距离的定义应当基于三角不等式，但是很多差异性的度量并不具有该属性，为了区别这些差异性度量和距离度量，我们称它们为‘相异度’”)）。由于它不满足三角不等式，我们应当称之为“相异度”而非“距离”）

布雷-柯蒂斯相异度和雅卡尔指数（英语：Jaccard index）相似，但是由于布雷-柯蒂斯相异度是半度量的，所以雅卡尔指数可能会是更好的选择。

2.canberra

Canberra distance是用来衡量两个向量空间的居间,是Manhattan distance的加权版本，Canberra distance已被用作比较排名列表和计算机安全中的入侵检测的测量。

通常堪培拉距离对于接近于0（大于等于0）的值的变化非常敏感。与马氏距离一样，堪培拉距离对数据的量纲不敏感。不过堪培拉距离假定变量之间相互独立，没有考虑变量之间的相关性。

3.chebyshev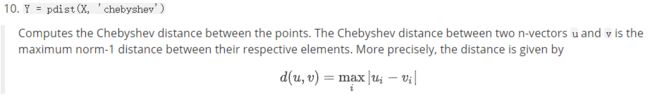

切比雪夫距离（Chebyshev distance）或是L∞度量是向量空间中的一种度量，两个点之间的距离定义为其各坐标数值差的最大值。以(x1,y1)和(x2,y2)两点为例，其切比雪夫距离为max(|x2-x1|,|y2-y1|)。切比雪夫距离得名自俄罗斯数学家切比雪夫。

4.cityblock

出租车几何或曼哈顿距离（Manhattan Distance）是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

5.correlation

皮尔逊相关系数（英語：Pearson correlation coefficient ，常用r或Pearson's r表示）用于度量两个变量X和Y之间的相关程度（线性相关），其值介于-1与1之间。在自然科学领域中，该系数广泛用于度量两个变量之间的线性相关程度。

皮尔逊距离度量的是两个变量X和Y，它可以根据皮尔逊系数定义成可以发现，皮尔逊系数落在[-1,1]，而皮尔逊距离落在 [0,2]。（因此文档钟指的是皮尔逊距离）

6.cosine

余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。

余弦相似度通常用于正空间，因此给出的值为0到1之间。注意这上下界对任何维度的向量空间中都适用，而且余弦相似性最常用于高维正空间。

两个向量间的余弦值可以通过使用欧几里得点积公式求出：

给定两个属性向量， A 和B，其余弦相似性θ由点积和向量长度给出：

类似皮尔逊相关系数，为了使得两个变量越相似，度量值越小。因此，这里余弦距离采用1-cos(Θ）。

7.dice

骰子系数（Dice coefficient）是一种集合相似度度量函数，通常用于计算两个样本的相似度：

和Jaccard类似，它的范围为0到1。 与Jaccard不同的是，相应的差异函数

不是一个合适的距离度量措施，因为它没有三角形不等性的性质。与Jaccard类似, 集合操作可以用两个向量 A 和B的操作来表示:

上式给出了两个向量的距离输出，也给出了更一般情况下向量之间的相似度度量措施。 Dice 系数可以计算两个字符串的相似度：Dice（s1,s2）=2*comm(s1,s2)/(leng(s1)+leng(s2))。 其中，comm (s1,s2)是s1、s2 中相同字符的个数leng(s1)，leng(s2)是字符串s1、s2 的长度。

8.euclidean

欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。在欧几里得空间中，点x =(x1,...,xn)和 y =(y1,...,yn)之间的欧氏距离为:

9.hamming

在信息论中，两个等长字符串之间的汉明距离（英语：Hamming distance）是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：1011101与1001001之间的汉明距离是2

10.jaccard

Jaccard相似指数用来度量两个集合之间的相似性，它被定义为两个集合交集的元素个数除以并集的元素个数。系数值范围在[0,1]，值越大，样本相似度越高。

Jaccard距离用来度量两个集合之间的差异性，它是Jaccard的相似系数的补集，被定义为1减去Jaccard相似系数。距离越小，样本相似度越高。

11.jensenshannon

计算两个一维概率数组之间的Jensen-Shannon距离(度量)。这是Jensen-Shannon散度的平方根。

两个概率向量p和q之间的Jensen-Shannon距离定义为:

其中m是逐点均值，p和q和D是Kullback-Leibler散度。如果p和q的总和不等于1.0，则此例程会将其标准化。

12.kulsinski

库尔辛斯基差异（Kulsinski dissimilarity）计算两个布尔一维数组之间的库尔辛斯基差异。两个布尔一维数组u和v之间的Kulsinski差异定义为

13.mahalanobis

马氏距离(Mahalanobis Distance)是度量学习中一种常用的距离指标，同欧氏距离、曼哈顿距离、汉明距离等一样被用作评定数据之间的相似度指标。但却可以应对高维线性分布的数据中各维度间非独立同分布的问题。马氏距离可以看作是欧氏距离的一种修正，修正了欧式距离中各个维度尺度不一致且相关的问题。

单个数据点的马氏距离：

数据点x, y之间的马氏距离：

其中Σ是多维随机变量的协方差矩阵，μ为样本均值，如果协方差矩阵是单位向量，也就是各维度独立同分布，马氏距离就变成了欧氏距离。

△马氏距离的问题：协方差矩阵必须满秩；不能处理非线性流形(manifold)上的问题

14.matching

15.minkowski

 闵可夫斯基距离（Minkowski distance）是衡量数值点之间距离的一种常见的方法。设n维空间中有两点坐标x, y，p为常数，闵式距离定义为：

• 当p=1时，得到绝对值距离，也叫曼哈顿距离（Manhattan distance）、出租汽车距离或街区距离（city block distance）。
• 当p=2时，得到欧几里德距离（Euclidean distance）距离，就是两点之间的直线距离（以下简称欧氏距离）。欧氏距离中各特征参数是等权的。
• 令p→∞切比雪夫距离。

△注意：闵氏距离与特征参数的量纲有关，有不同量纲的特征参数的闵氏距离常常是无意义的。闵氏距离没有考虑特征参数间的相关性，而马哈拉诺比斯距离解决了这个问题。

16.rogerstanimoto

田本罗杰斯差异（Rogers-Tanimoto dissimilarity）

，其中

17.russellrao

拉塞尔差异（Russell-Rao dissimilarity）

18.seuclidean

19.sokalmichener

索卡尔米切纳差异（Sokal-Michener dissimilarity）

，其中，

20.sokalsneath

索卡尔雪差异（Sokal-Sneath dissimilarity）

，其中，

21.sqeuclidean

22.yule

Yule差异（Yule dissimilarity）
 ，其中，

参考:

[1]百度百科、维基百科

[2][机器学习]常用距离定义与计算

[3]机器学习领域 几种距离度量方法【3】

[4]python scipy spatial.distance.jensenshannon用法及代码示例

[5]python scipy spatial.distance.kulsinski用法及代码示例

[6]马氏距离(Mahalanobis Distance)