文献阅读:Linformer: Self-Attention with Linear Complexity
- 文献阅读:Linformer: Self-Attention with Linear Complexity
- 1. 问题描述
- 2. 核心方法
- 1. vanilla attention layer
- 2. attention优化
- 3. 分析 & 证明
- 1. self-attention是低阶的
- 2. linear self-attention效果与vanilla self-attention相仿
- 3. 实验
- 1. 预训练效果考察
- 2. 下游任务效果
- 3. 时间优化考察
- 4. 结论 & 思考
- 文献链接:https://arxiv.org/pdf/2006.04768.pdf
1. 问题描述
这篇文章同样是我在阅读Transformer Quality in Linear Time这篇文章时想到的一个工作,所以就来考个古,把这篇文章也翻出来整理一下,算是给自己做个笔记了。
Linformer这篇工作是20年facebook提出来的一个工作,目的是优化transformer的计算量,尤其是针对长句计算希望可以减少计算的复杂度,同时尽可能地保持模型的效果。
众所周知,self-attention layer的计算复杂度是和句长成正比关系的,这就导致transformer在针对长句的计算上面尤其耗时,几乎不具备可用性。
当然,针对这方面已经有了不少优化,比如从算子算力方面的半精度模型优化,或者另辟蹊径用蒸馏方式来直接用小模型替代大模型。
而对于模型本身的优化,也同样有sparse transformer以及reformer这样的工作在前。Linformer算是另一种针对模型的attention结构本身进行优化的一种方式。
他的核心思路就是直接先将attention投影到一个低阶矩阵,从而在计算attention时避免掉 O ( n 2 ) O(n^2) O(n2)的计算量,而是转换成 O ( k ⋅ n ) O(k\cdot n) O(k⋅n)的计算量( k k k是一个事先确定的常数),从而使得模型存在对长句的编码能力。
我们摘取文中对当时所有方法以及对应的复杂度总结表格如下:
2. 核心方法
1. vanilla attention layer
在介绍Linformer的核心结构之前,我们首先回顾一下基础的transformer的attention layer的结构。
为了简化问题,我们这里暂时不考虑多头的情况。
我们可以直接写出attention层的表达公式如下:
f ( Q , K , V ) = s o f t m a x ( Q W Q ⋅ ( K W K ) T d ) V W V f(Q, K, V) = softmax(\frac{QW_Q \cdot (KW_K)^T}{\sqrt{d}})VW_V f(Q,K,V)=softmax(dQWQ⋅(KWK)T)VWV
针对self-attention的情况,我们假设句长为 n n n,embedding维度为 d d d,则 Q , K , V ∈ R n × d Q, K, V \in \mathbb{R}^{n\times d} Q,K,V∈Rn×d, W Q , W K , W V ∈ R d × d W_Q, W_K, W_V \in \mathbb{R}^{d \times d} WQ,WK,WV∈Rd×d。
因此,当 n ≫ d n \gg d n≫d时,上述的attention层的算法复杂度就是 O ( n 2 ) O(n^2) O(n2)。
2. attention优化
Linformer的核心方法其实还是比较trivial的,本质上就是将attention投影到一个低阶矩阵当中,从而规避掉 O ( n 2 ) O(n^2) O(n2)的attention计算。
具体而言,我们在attention计算中增加两个矩阵E和F,使得n阶的attention降维到固定的k维矩阵:
f ( Q , K , V ) = s o f t m a x ( Q W Q ⋅ ( E ⋅ K W K ) T d ) ( F ⋅ V W V ) f(Q, K, V) = softmax(\frac{QW_Q \cdot (E \cdot KW_K)^T}{\sqrt{d}})(F \cdot VW_V) f(Q,K,V)=softmax(dQWQ⋅(E⋅KWK)T)(F⋅VWV)
其中, E , F ∈ R k × n E, F \in \mathbb{R}^{k \times n} E,F∈Rk×n, k k k是一个常数。
由此,我们就可以将 O ( n 2 ) O(n^2) O(n2)的计算复杂度降维到 O ( k n ) O(kn) O(kn),其中 k k k不过是一个常数而已。
更进一步的,为了更进一步的缩小参数量,文中还尝试了在不同的层之间share相同的 E , F E,F E,F,甚至干脆令 E = F E = F E=F。
令人惊讶的是,这样同样可以得到一个还过得去的效果,简直震惊。
3. 分析 & 证明
有了上面这个看似粗暴的手法,下面,我们来看看上述方法是否在逻辑上合理。
1. self-attention是低阶的
首先,上述attention投影的基础在于一个现象,即:
- self-attention的权重矩阵是一个低阶矩阵。
也就是说,如果我们跑去计算一下权重矩阵的本征值,我们可以发现,得到的大部分本征值都是0或者接近于0的。
文中给出了一个图表来对这个现象进行了展示:
可以看到,尾部有相当一部分的本征值事实上是接近于0的。
更数学化的,文中还给出了一个定理以及其对应的推导,不过这里就不过多展开了,就只把相应的定理摘录如下:
Theorem 1. (self-attention is low rank)
For any Q , K , V ∈ R n × d Q, K, V \in \mathbb{R}^{n \times d} Q,K,V∈Rn×d, and W Q , W K , W V ∈ R d × d W_Q, W_K, W_V \in \mathbb{R}^{d \times d} WQ,WK,WV∈Rd×d, for any column vector w ∈ R n w \in \mathbb{R}^n w∈Rn of matrix V W V VW_V VWV, there exists a low-rank matrix P ~ ∈ R n × n \tilde{P} \in \mathbb{R}^{n\times n} P~∈Rn×n such that
P r ( ∣ ∣ P ~ w T − P w T ∣ ∣ < ϵ ∣ ∣ P w T ∣ ∣ ) > 1 − o ( 1 ) Pr(||\tilde{P}w^T - Pw^T|| < \epsilon||Pw^T||) > 1 - o(1) Pr(∣∣P~wT−PwT∣∣<ϵ∣∣PwT∣∣)>1−o(1)
and r a n k ( P ~ ) = Θ ( l o g ( n ) ) rank(\tilde{P}) = \Theta(log(n)) rank(P~)=Θ(log(n)).
where the context mapping matrix P P P is defined as:
P = s o f t m a x ( Q W Q ⋅ ( K W K ) T d ) P = softmax(\frac{QW_Q \cdot (KW_K)^T}{\sqrt{d}}) P=softmax(dQWQ⋅(KWK)T)
2. linear self-attention效果与vanilla self-attention相仿
有了上述定理,那么,我们总可以找到一个低阶的attention权重矩阵 P ~ \tilde{P} P~来替换掉原始的 P P P,但是,我们如何来寻找这个低阶矩阵呢?
或者说,我们在上一个小节当中已经给出的那个暴力的降维方案,是否真的可以达到相仿的效果呢?
同样的,文中依然给出了一个数学证明,不过这里同样还是不具体展开了,只是摘录文中的定理如下:
Theorem 2. (Linear self-attention)
For any Q , K , V ∈ R n × d Q, K, V \in \mathbb{R}^{n \times d} Q,K,V∈Rn×d and W Q , W K , W V ∈ R d × d W_Q, W_K, W_V \in \mathbb{R}^{d \times d} WQ,WK,WV∈Rd×d,
if k = m i n Θ ( 9 d l o g ( d ) ) / ϵ 2 , 5 Θ ( l o g ( n ) / ϵ 2 ) k = min{\Theta(9d log(d))/ \epsilon^2, 5 \Theta(log(n)/\epsilon^2)} k=minΘ(9dlog(d))/ϵ2,5Θ(log(n)/ϵ2), then there exists matrices E , F ∈ R n × k E, F \in \mathbb{R}^{n \times k} E,F∈Rn×k such that,
for any row vector w w w of matrix Q W Q ( K W K ) T / d QW_Q(KW_K)^T/\sqrt{d} QWQ(KWK)T/d, we have:
P r ( ∣ ∣ s o f t m a x ( w E T ) F V W V − s o f t m a x ( w ) V W V ∣ ∣ ≤ ϵ ∣ ∣ s o f t m a x ( w ) ∣ ∣ ⋅ ∣ ∣ V W V ∣ ∣ ) > 1 − o ( 1 ) Pr(||softmax(wE^T)FVW_V - softmax(w)VW_V|| \leq \epsilon||softmax(w)|| \cdot ||VW_V||) > 1 - o(1) Pr(∣∣softmax(wET)FVWV−softmax(w)VWV∣∣≤ϵ∣∣softmax(w)∣∣⋅∣∣VWV∣∣)>1−o(1)
只能说套公式简单,真的要做研究的话,数学真的是太重要了……
3. 实验
现在,介绍完了具体的方法,我们来考察一下文中的实验以及其效果。
1. 预训练效果考察
首先,作者考察了一下Linformer在与训练任务当中的ppl效果,得到结果如下:
可以看到:
- 从图a可以看出,除了在 k = 64 k=64 k=64时性能还是能看出差异之外,当 k k k取128和256时差异事实上和原版的transfromer都不太大;
- 从图b可以看出,当句长增加时,1中的结论依然成立,即 k = 128 k=128 k=128时效果依然可以媲美原版的transformer的效果;
- 从图c可以看到,对 E , F E,F E,Fshare参数不会对效果产生太大的影响,因此不同层之间可以share参数,且 E , F E,F E,F可以同同一个矩阵来表示;
- 最后,从图d可以看到,Linformer在长句情况下也能够获得很好的训练;
2. 下游任务效果
除了对于单纯的预训练任务,文中还进一步考察了其在下游finetune任务当中的效果,毕竟如果无法在下游任务当中获得较好的表现那么这个模型事实上也是多少有失偏颇的。
作者在语义情感分类(SST-2,IMDB)、推理(ONLI)以及文本相似度(QQP)任务下进行了结果考察,得到结果如下:
可以看到,Linformer的效果完全不输于原版的Roberta模型。
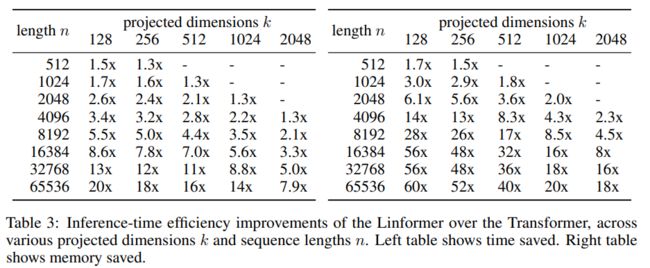
3. 时间优化考察
最后,文中作者还考察了一下Linformer在推理速度上能够带来的效率提升,毕竟这个优化的核心目的还是说能够在不损失效果的情况下优化模型的推理速度。
实验得到的结果如下表所示:
可以看到:
- 确实如预期一样,Linformer可以带来足量的时间复杂度以及空间复杂度上的效果提升,尤其在长句的情况下,效果尤为明显。
4. 结论 & 思考
综上,我们可以看到,本质上来说Linformer就是基于attention矩阵稀疏性的特征,先对其进行了一次降维投影,从而大幅减少了模型的计算量,同时最大幅度地保留了模型的性能。
文中的方法本身是比较简单的,不过对应的数学分析确实是厉害。
不过anyway,毕竟对于我们而言,能够复用其工作才是核心所在,而Linformer显然是一个非常友好的方法,如果后面有遇到长句的文本处理任务的话,倒是可以试试Linformer的方法,估计能够带来一定的收益。