八数码问题
八数码问题
八数码问题:
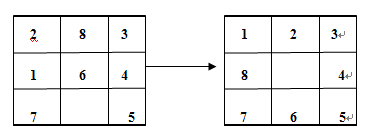
我想大家小时候一定玩过八数码的游戏,如下图:在一个九宫格里面放入8个数字,数字只能上下左右移动,并且只能移动到空白处。通过若干此移动后,能把数字移动成图1.1右方所示图案。
图1.1(左边为开始格局,右边为移动后最终格局
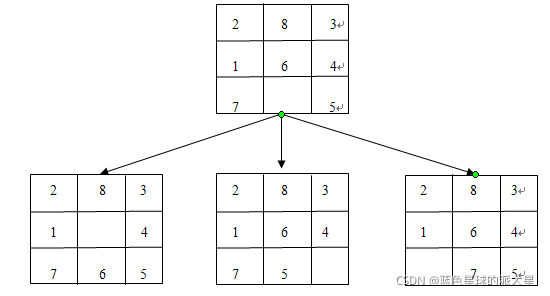
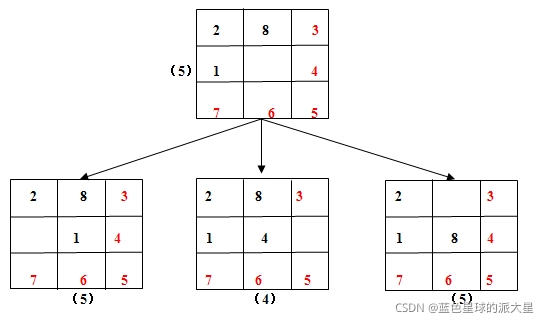
下图是图1.1下一个格局的三种情况:
如果按正常的思维,采用盲目搜索的话,不仅搜索的次数多,而且往往容易陷入死循环中,所以面对此问题需要一种策略——启发式搜索
启发式搜索:启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率
解决此问题的启发策略:
每次移动的时候,正确位置数码的个数要大于交换前正确位置数码个数。
正确位置数码个数:每个数码的位置与最终格局的对比,如果位置相同,则说明此数码在正确位置。
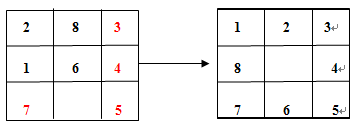
如下图:
图1.3
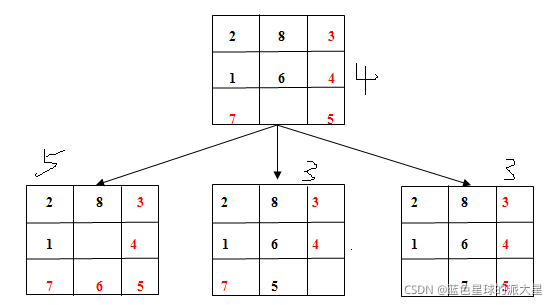
图1.3中右边为最终格局,左边为当前格局,红色字体标识的数码为 正确位置数码,由此可以发现其正确位置的数码个数为4个。那么图1.2中正确数码如下图所示:
由上图所示可得,正确位置数码个数大于等于4的只有左下方的格局,那么下一步选择的就是左下方的格局,再次调用次算法如下图:
BFS+Cantor 解决方法
#include
const int LEN = 362880; //状态共9!=362880种
using namespace std;
struct node
{
int state[9]; //记录一个八数码的排列,即一个状态
int dis; //记录到起点的距离
};
int dir[4][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
//左,上,右,下顺时针方向,左上角的坐标是(0,0)
int visited[LEN] = {0}; //与每个状态对应的记录,Cantor()函数对它置数,并判重
int start[9]; //开始状态
int goal[9]; //目标状态
long int factory[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // Cantor()用到的常数 即阶乘
//用康托展开判重
bool Cantor(int str[], int n)
{
long result = 0;
for (int i = 0; i < n; i++)
{
int counted = 0;
for (int j = i + 1; j < n; j++)
{
//当前未出现的元素排在第几个
if (str[i] > str[j])
++counted;
}
result += counted * factory[n - i - 1];
}
if (!visited[result]) //没有被访问过
{
visited[result] = 1;
return 1;
}
else
return 0;
}
int bfs()
{
node head;
memcpy(head.state, start, sizeof(head.state)); //复制起点的状态
head.dis = 0;
queue q; //队列中的内容是记录状态
Cantor(head.state, 9); //用康托展开判重,目的是对起点的visited[]赋值
q.push(head); //第一个进队列的是起点状态
while (!q.empty()) //处理队列
{
head = q.front();
q.pop(); //可在此处打印head.state,看弹出队列的情况
int z;
for (z = 0; z < 9; z++) //找到这个状态中元素0的位置
{
if (head.state[z] == 0) //找到了
break;
}
int x = z % 3; //横坐标
int y = z / 3; //纵坐标
for (int i = 0; i < 4; i++) //上,下,左,右最多可能有4个新状态
{
int newx = x + dir[i][0]; //元素0转移后的新坐标
int newy = y + dir[i][1];
int nz = newx + 3 * newy; //转化为一维
if (newx >= 0 && newx < 3 && newy >= 0 && newy < 3) //未越界
{
node newnode;
memcpy(&newnode, &head, sizeof(struct node)); //复制这个新状态
swap(newnode.state[z], newnode.state[nz]); //把0移动到新的位置
newnode.dis++;
if (memcmp(newnode.state, goal, sizeof(goal)) == 0) //与目标状态对比
return newnode.dis; //到达目标状态,返回距离,结束
if (Cantor(newnode.state, 9)) //用康托展开判重
q.push(newnode); //把新的状态放入队列
}
}
}
return -1; //没找到
}
int main()
{
for (int i = 0; i < 9; i++) //初始状态
cin >> start[i];
for (int i = 0; i < 9; i++) //目标状态
cin >> goal[i];
int num = bfs();
if (num != -1)
cout << num << endl;
else
cout << "Impossible" << endl;
return 0;
}
A* + Set 解决方法
#include
using namespace std;
const int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
int fx, fy;
char ch;
struct Matrix
{
int e[5][5];
bool operator<(Matrix x) const
{
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
if (e[i][j] != x.e[i][j])
return e[i][j] < x.e[i][j];
return false;
}
} first, standard;
// 函数h可以定义为,不在应该在的位置的数字个数。
// 容易发现h满足以上两个性质,此题可以使用 A*算法求解。
int h(Matrix m)
{
int ret = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
if (m.e[i][j] != standard.e[i][j])
ret++;
return ret;
}
struct node
{
Matrix matrix;
int t;
bool operator<(node x) const { return t + h(matrix) > x.t + h(x.matrix); }
} x;
priority_queue qu; //搜索队列
set st; //防止搜索队列重复
int main()
{
standard.e[1][1] = 1; //定义标准表
standard.e[1][2] = 2;
standard.e[1][3] = 3;
standard.e[2][1] = 8;
standard.e[2][2] = 0;
standard.e[2][3] = 4;
standard.e[3][1] = 7;
standard.e[3][2] = 6;
standard.e[3][3] = 5;
for (int i = 1; i <= 3; i++) //输入
for (int j = 1; j <= 3; j++)
{
scanf(" %c", &ch);
first.e[i][j] = ch - '0';
}
qu.push({first, 0});
while (!qu.empty())
{
x = qu.top();
qu.pop();
if (!h(x.matrix))
{ //判断是否与标准矩阵一致
printf("%d\n", x.t);
return 0;
}
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
if (!x.matrix.e[i][j])
fx = i, fy = j; //如果该点上的数不为0
for (int i = 0; i < 4; i++)
{ //对四种移动方式分别进行搜索
int xx = fx + dx[i], yy = fy + dy[i];
if (1 <= xx && xx <= 3 && 1 <= yy && yy <= 3)
{
swap(x.matrix.e[fx][fy], x.matrix.e[xx][yy]);
if (!st.count(x.matrix))
st.insert(x.matrix),
qu.push({x.matrix, x.t + 1}); //这样移动后,将新的情况放入搜索队列中
swap(x.matrix.e[fx][fy], x.matrix.e[xx][yy]); //如果不这样移动的情况
}
}
}
return 0;
}