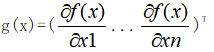机器学习-梯度下降算法

4.3.3梯度的计算

    梯度下降在机器学习中应用十分的广泛，不论是在线性回归还是逻辑回归中，梯度就是表示某一函数在该点处的方向导数沿着该方向取得最大值即函数在该方向的导数，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

本文将从一个下山的场景开始，先提出梯度下降算法的基本思想，进而从数学上解释梯度下降算法的原理，解释为什么要用梯度，最后实现一个简单的梯度下降算法的实例。

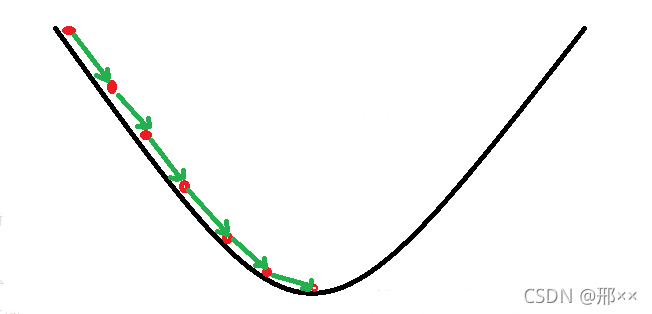
    梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；同理上山也是如此，只是这时候就变成梯度上升算法了。

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢？接下来，我们从微分开始讲起：

 

首先给出一个问题：给定如上图一个函数f(x)，求f(x)的最小值。根据我们的大学数学知识我们知道，可以先对函数求导，然后再求驻点，最后比较驻点处的函数值，即可得出最小值。但显然这不是我们想要的求解方式，我们要学习的是机器学习，我们的目的是让计算机来得出结果。

  那么在我们的大学数学学习中除了上述的解析法之外，还有一个数值解法，即下山法。

步骤一：赋初值x=x0

步骤二：随机生成增量∆x（增量方向也是随机的）

步骤三：若f(x+∆x)

步骤四：重复步骤二和三至收敛

对于多元函数f(x,y)(此处以二元为例)，有类似的下山算法：

步骤一：赋初值x=x0,y=y0

步骤二：随机生成增量∆x，∆y（增量方向也是随机的）

步骤三：若f(x+∆x,y+∆y)

步骤四：重复步骤二和三至收敛

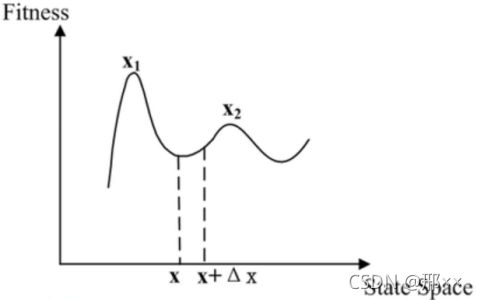
从爬山法求最小值中我们可以发现存在一些问题：

1. 初值x0的设定对收敛快慢影响很大
2. 增量∆的方向随机生成，效率较低。步长太小则计算效率低，太大容易越过极值点
3. 容易显然局部最优（函数多个波谷的情况）
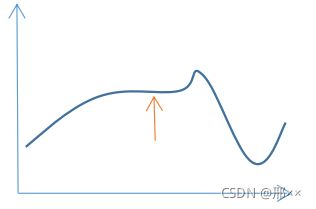
4. 无法处理“高原”和“山脊”的情况。

                       “高原”的情况

爬山法可改进的点：

根据函数的特性，确定每一次迭代的增量方向和搜索步长

记第k轮迭代后，自变量取值x=xk,利用泰勒公式将f(x)在xk处展开：

f(x)=f(xk)+f’(xk)(x-xk)+R(x)

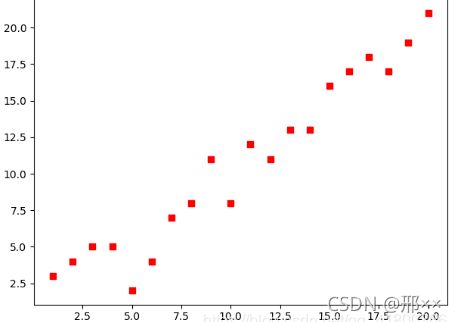
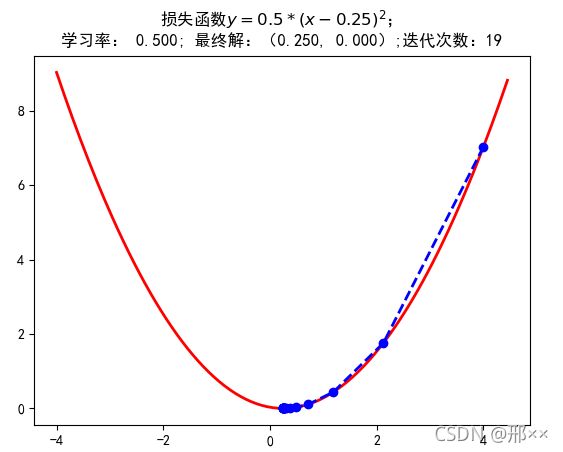
在第（k+1）轮迭代后，我们希望f(xk+1)

f(xk+1)-f(xk)=f’(xk)(xk+1-xk)<0

若f’(xk)>0,则需要xk+1-xk<0;若f’(xk)>0，则需要xk+1-xk<0。

根据这种需要我们可以构造出满足要求的xk+1

xk+1-xk = -f’(xk)

根据f(xk+1)-f(xk)=f’(xk)(xk+1-xk)

从而通过下面不等式可以验证，迭代方向始终是正确的方向即往下山的方向

f(xk+1)-f(xk)=-[f’(xk)]2 <0 每次的函数值都减小了

另外，若|f’(xk)|的值很大，会使xk+1偏离xk很远，从而使泰勒公式不成立，因此通常引入一个很小的系数γ>0来减小偏移程度

xk+1-xk = -γf’(xk)

因此我们就得到了迭代公式

xk+1= xk -γf’(xk)

对于多元函数，利用多元函数的泰勒公式，有类似的分析过程，迭代公式为

xk+1= xk -γg(xk)

其中x=（x1 ... xn）T是n维向量，

成为多元函数f(x)的梯度（向量），γ>0称为步长或学习速率，所以该优化方法称为梯度下降法。

梯度下降法相较于爬山法：

1. 解决了每一轮迭代自变量的更新方向问题，计算效率更高
2. 步长可通过一维柱搜索确定，即通过求一元函数f(xk -γg(xk))-f(xk)的极小值确定（γ>0是唯一的自变量）。在实际应用中，一般依靠经验设定一个较小的常数步长。
3. 梯度下降法本身无法解决初值设定带来的全局最优和局部最优问题。
4. 如果是求函数的极大值，则推导过程类似，只是迭代公式中的符号改变，称为梯度上升法xk+1= xk +γg(xk)

4.3.4 梯度下降法求最小值

    使用python实现一个简单的梯度下降算法求损失函数的最小值并作出回归直线。场景是一个简单的线性回归的例子：假设现在我们有一系列的点（数据集），如下图所示：

我们将用梯度下降法来拟合出这条直线。首先，我们需要定义一个代价函数，在此我们选用均方误差代价函数（也称平方误差代价函数）

对该公式注释如下：

  （1）m是数据集中数据点的个数，也就是样本数

（2）½是一个常量，这样是为了在求梯度的时候，二次方乘下来的2就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响

（3）y 是数据集中每个点的真实y坐标的值，也就是类标签

（4）h 是我们的预测函数（假设函数），根据每一个输入x，根据计算得到预测的y值，即 

明确了代价函数和梯度，以及预测的函数形式。我们就可以开始编写代码了。为了方便理解我们假设代价函数为开口向上的一个凹函数y = 0.5 * (x-0.25)^2 所有代码如下：

import numpy as np

import matplotlib as mpl

import matplotlib.pyplot as plt

mpl.rcParams['font.family'] = 'sans-serif'

mpl.rcParams['font.sans-serif'] = 'SimHei'

mpl.rcParams['axes.unicode_minus'] = False

# 构建一维的损失函数

def f1(x):

    return 0.5 * (x-0.25) ** 2   # 假设一个开口向上的损失函数

def h1(x):

    return 0.5 * 2 * (x-0.25)  # 原函数的一阶导数

# 使用梯度下降法进行解答

GD_X = []  # 存每次迭代坐标的x值

GD_Y = []  # 存每次迭代坐标的y值

x = 4  # 相当于x0,即开始迭代的位置

alpha = 0.5  # 步长或者学习率

f_change = f1(x)  # 初始值为x0处的y值，用于后面判断判断迭代条件的y的迭代后的变化不能太小

f_current = f_change  # y的变化，作用是作为一个递归的条件判断

GD_X.append(x)  # 将坐标x的值存放进列表

GD_Y.append(f_current)  # 将坐标y的值存放进列表

# 迭代次数

iter_number = 0  # 迭代次数初始值为0

while f_change > 1e-10 and iter_number < 100:  # 迭代继续进行的条件，避免无线迭代下去

    iter_number += 1

    x = x - alpha * h1(x)  # 迭代一次后的x值

    tmp = f1(x)  # 迭代一次后的y值

    # 判断y值的变化，不能太小

    f_change = np.abs(f_current - tmp)

    f_current = tmp  # 更新更新当前坐标的y值

    GD_X.append(x)  # 将坐标x的值存放进列表

    GD_Y.append(f_current)  # 将坐标y的值存放进列表

print('最终的结果：（%.5f,%.5f）' % (x, f_current))

print('迭代次数是：%d' % iter_number)

print(GD_X)

# 构建数据

X = np.arange(-4, 4.5, 0.05)

Y = np.array(list(map(lambda t: f1(t), X)))

# 画图

plt.figure(facecolor='w')

plt.plot(X, Y, 'r-', linewidth=2)

plt.plot(GD_X, GD_Y, 'bo--', linewidth=2)

plt.title('损失函数$y=0.5*(x-0.25)^2$； \n学习率： %.3f; 最终解：（%.3f, %.3f）;迭代次数：%d'% (alpha, x, f_current, iter_number))

plt.show()

运行结果如下图：

 

代码引自《白话机器学习的数学》