深度学习部分优化算法详解

 前言

由于本人在进行深度学习的初期，因为对迭代方式的不理解，造成了极大的停滞期。在使用网络的过程中，因为只懂如果应用，不懂如何改进细节或不懂在优化算法中出现不合适后如何选择新的优化算法，所以着重学习了优化算法的数学原理。本文会讲解梯度下降、随机梯度下降、小批量随机梯度下降、动量法梯度下降。其他的优化算法比如AdaGrad、RMSProp、AdaDelta、Adam

优化算法

首先了解下优化算法在深度学习中的重要作用

在深度学习的训练中，需要不断迭代模型的参数以让损失函数的结果得到预期的效果。那么，在迭代的过程中，就是以统称为优化算法的数学公式来实现。本人学习深度学习使用的是《动手学深度学习》，该书数学原理都十分详细，适合初学者或者想了解深度学习内部原理的人。

在模型和损失函数形式较为简单时，误差最小化的问题的解可以直接用公式表达出来，这类解又叫做解析解。本篇博客出现的优化算法解均为解析解。然而大部分的深度学习模型并没有解析解(因为太复杂)，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值，这类解叫数值解。

该图为本人所认知的深度学习简要流程概括，其中最关键的就是从使用训练数据集通过优化算法不断迭代参数w，降低loss。那么在迭代过程中使用的数学公式，关键就在于优化算法的选择了。

梯度下降

梯度下降在深度学习中很少被直接引用，更多的是以其为原型构造出各种适合多问题的各类模型。但是理解梯度下降、反向更新数据是学习其他优化算法的基础，并且也很有利于理解深度学习。以最简单的一维标量来推导梯度下降的公式，来观察梯度下降可以通过迭代的方式降低目标函数值的原因：

给定一个绝对值足够小的数(与高等数学极限中所提到的足够小的数含义相同)，凭借泰勒公式展开项，可以得到一个展开式：

是在x处的梯度，因为此时x为一维标量，所以也可以称为导数。

我们再引入一个足够小的常数，使得>0，我们将替换成。得到

如果，那么，原式就变成

对于它的参数x来说，就存在

在深度学习的学习中，总会围绕一个词学习率，其实就是所说的学习率。

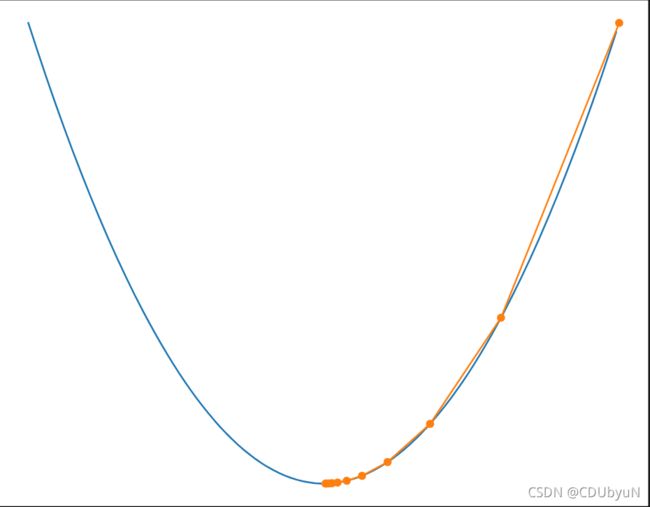
我们以为例来看一下梯度下降的下降方式

学习率eta设置成0.2。

调用的包统一在这里给出：

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, nd, init, gluon
from mxnet.gluon import data as gdata, loss as gloss
import numpy as np
import math

def gd(eta):
    x = 10
    results = [x]
    for i in range(10):
        x -= eta * 2 * x
        results.append(x)
    print(f'epoch 10, x:{x}')
    return results

def show_trace(res):
    n = max(abs(min(res)), abs(max(res)), 10)
    f_line = np.arange(-n, n, 0.1)
    d2l.set_figsize(figsize = (10, 8))
    d2l.plt.plot(f_line, [x * x for x in f_line])
    d2l.plt.plot(res, [x * x for x in res], '-o')
    d2l.plt.xlabel('x')
    d2l.plt.ylabel('f(x)')

eta = 0.2
res = gd(eta)
show_trace(res)

 梯度下降存在一些问题，比如一些人在梯度下降的过程中，参数是呈发散趋势的，损失函数得到的结果甚至会越来越大，这是为什么呢? 我把上述的代码加了一些改进，让我可以比较学习率不同时发生的变化。

learning_list = np.arange(0.1, 1.1, 0.1)
res = []
for i in range(len(learning_list)):
    res.append(gd(learning_list[i]))
    show_trace(res[i])

可以看到随着学习率不断增大，出现了图像来回震荡，而且还有一些还没有达到最优解，就停止了。或许有人已经想到下面的图了，难道只能让图像不断收敛吗？当学习率过大的时候，通过公式显而易见，参数值越来越大了。我们把学习率调到2看一下

可以发现，目标函数的值已经呈发散趋势了。这也暴露了梯度下降的弊端，学习率十分影响模型的训练。

从一维到二维，从标量到向量

在引入其他的优化算法之前，我们先把思想从一维上升到二维，从输入标量到向量(但是输出依然是标量)

先将刚才在梯度下降中的公式进行优化：

用代替，正如上文所说，在一维标量的计算中，梯度是可以跟导数相等的。

新的函数的参数

目标函数y的梯度

梯度中每个偏导数都代表了函数在每个方向上有关方向的变化率。为了测量f在单位向量上的变化率，在多元微积分中介绍了方向导数的公式：

根据方向导数的性质可以把公式改写成

方向导数给出了f(x)在各个方向上的变化率，而我们想做的事是最小化f，梯度是方向导数方向上最大的取值，且方向相同。

因此，我们可能通过梯度下降算法来不断降低函数f的值:

随机梯度下降

在求数值解的优化算法中，随机梯度下降(SGD)备受青睐，它的算法很简单却得到了广泛应用。我们继续多维梯度下降的逻辑，想象一个事情。每次自变量迭代的计算开销都为，它随着n线性增长。因此，当训练数据样本数足够大时，梯度下降每次迭代的计算开销很高。

SGD减少了每次迭代的次数，与梯度下降不同的是，在SGD的迭代过程中，会随机均匀抽取其中的一个样本索引。所以，它的计算开销只有常数。

迭代公式：（样本索引 ）

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

必须要强调的就是，随机梯度下降每次计算量是常数1，但是所花费的时间比梯度下降少得多。而且，在通常的运算中，我们习惯在迭代过程中，添加噪声项。在实际中，这些噪声项通常指训练数据集中无意义的干扰。

下面来通过一个二维向量的函数来观察梯度下降与随机梯度下降的不同。

二维向量，目标函数

------------------------------------------------------------------------------------------

首先，我们使用梯度下降

# 用来保存迭代的点

def train_2d(trainer):
    x1, x2 = -5, -2
    results = [(x1, x2)]
    for i in range(20):
        x1, x2 = trainer(x1, x2)
        results.append((x1, x2))
    print(f'epoch {i+1}, x1 {x1}, x2 {x2}')
    return results

def show_trace_2d(f, results):
    d2l.set_figsize(figsize = (10, 8))
    d2l.plt.plot(*zip(*results), '-o', color = '#ff7f0e')
    # *的用法
    x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
    d2l.plt.contour(x1, x2, f(x1, x2), color = '#1f77b4')
    # contour 等高线、轮廓
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')

学习率我们设置为0.1，使用梯度下降连续更迭20次后，可以发现最终接近最终解[0, 0]

同样的，在这里也可以通过调试学习率来让其图像变得更加“曲折”，这里就不展示了。

我们再使用随机梯度下降，上文也提到随机梯度下降与梯度下降不同的地方，是存在噪音项，那么我们需要重新定义一下迭代的公式。

eta = 0.1

def sgd_2d(x1, x2):
    return (x1 - eta * (2 * x1 + np.random.normal(0, 1)),
            x2 - eta * (4 * x2 + np.random.normal(0, 1)))


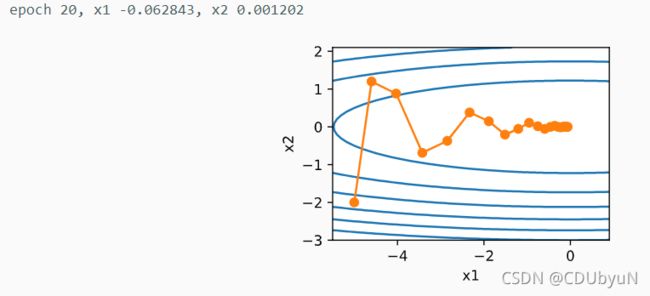
show_trace_2d(f_2d, train_2d(sgd_2d))

 显然，由于噪声项的出现，相比于梯度下降，SGD的图像更为曲折。

小批量随机梯度下降

因为梯度下降的过程中要使用全部的数据集，所以梯度下降也叫做批量梯度下降。

而随机梯度下降要求只能随机抽取一个样本。

那么很容易就会想到一件事情：每次从数据集中抽出一部分，而这种概念就是小批量随机梯度下降的原型。可以说，在不考虑噪音项的前提下，梯度下降，随机梯度下降，小批量随机梯度下降，三者是存在区间划分的。实际上他们的迭代方式基本相同。

下面先来描述一下小批量随机梯度下降：

在此之前，需要引入新的超参数---时间步和小批量。

小批量来自于训练样本的索引，我们可以通过重复采样或者不重复采样得到一个小批量中的各个样本。

通常，我们用batch_size来表示小批量的大小（后文都将用batch_size来表示）。在训练模型之前，规定了batch_size后，构建出来的模型会将原本的、全部的数据样本（设置为n）分割成  份。每一次更新数据就像把预先分割成一份份的数据样本放入设计好的训练模型中，显而易见，需要放回的次数就为。

所以说，小批量能够决定每次迭代时的数据（loss函数）更新次数。 

前者允许小批量数据中出现重复的样本，后者不能且更常见，不管是哪个，都有：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

对自变量迭代：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

当批量较小时，每次迭代使用的样本少，到底并行处理和内存使用效率变低，这可能使得计算同样样本的情况下比使用更大批量时所画时间更多。而当批量较大时，每个小批量梯度里可能含有更多的无用信息。为了更好的解，除了可以调节小批量大小、学习率以外，还可以增大迭代周期数。

为了能更兼容地在一个模型中实现三种梯度下降方法，来重新涉及一个新的训练模型。

def sgd(params, states, hyperparams):
    for p in params:
        p -= hyperparams['lr'] * p.grad
# 这里使用的数据类型是：NDArray
# 它特有的一个属性grad表示其梯度的值

def train_ch_more(trainer_fn, states, hyperparams, features, labels
                     batch_size = 10, num_epochs = 2):
    # 模型初始化
    net, loss = d2l.linreg, d2l.squared_loss
    # 参数的设置
    w = nd.random.normal(scale = 0.01, shape = (features.shape[1], 1))
    b = nd.zeros(1)
    # 为自动求梯度先申请空间
    w.attach()
    b.attach()
    
    # 平均损失函数
    def eval_loss():
        return loss(net(features, w, b), labels).mean().asscalar()
    ls = [eval_loss()]
    data_iter = gdata.DataLoader(gdata.ArrayDataset(features, labels), batch_size,
                                shuffle = True)
    for _ in range(num_epochs):
        # 记录开始时的时间
        start = time.time()
        # 此处体现批量大小对于迭代过程的影响
        for batch_i, (X, y) in enumerate(data_iter):
            with autograd.record():
                l = loss(net(X, w, b), y).mean() # 平均损失
            l.backward() # 自动求梯度
            train_fn([w, b], states, hyperparams)
            if (batch_i + 1) * batch_size % 10 == 0:
                ls.append(eval_loss()) # 每十个样本记录下当前训练误差
    print(f'loss: {ls[-1]} {time.time() - start} sec per epoch')‘

    # 画图
    d2l.set_figsize(figsize = (8, 6))
    d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    d2l.plt.xlabel('epoch')
    d2l.plt.ylabel('loss')

def train_sgd(lr, batch_size, num_epochs = 2):
    train_ch_more(lr, None, {'lr' = lr}, features, lables, batch_size, num_epochs)

综上，直接在train_sgd中设置参数就可以有效的控制批量的大小、学习率、迭代周期

我们使用一个来自NASA的测试不同飞机机翼噪音的数据集来对比三者的区别。

当函数中batch_size的参数为1500时，模型为梯度下降，梯度下降每个迭代周期只会迭代模型参数一次。（因为NASA的数据集含有1500个样本）并在多次迭代后趋于平稳。

train_sgd(1, 1500, 6)

 batch_size设置成1时，模型就是sgd，每次只会处理一个样本，所以一个周期要进行1500次更新。

train_sgd(0.005, 1)

 当batch_size为10时，优化使用的就是小批量梯度下降。

train_sgd(0.05, 10)

 总结，相同的数据集中三种优化方式的区别。

	loss	time
梯度下降	0.246	0.025s
随机梯度下降	0.247	2.180s
小批量随机梯度下降	0.244	0.253s

为什么随机梯度下降的用时，比其他两种方法多这么多？

虽然，三者在迭代过程中都处理了总共1500个样本的数据。但是，sgd在迭代过程中做了过多次的自变量自身迭代，而另外两者可以有效的利用矢量进行计算，而自变量本身这种办法并不有效。

学习率迭代

因为随机采样得到的梯度的方差在迭代过程中不会改变。（挖坑）

其实，在训练过程中，学习率本身也可以进行迭代。

通常，迭代的方式有两种：(通常 或者)或(如)

小总结

以上的三种优化算法，从本质上其实是相同的。只是需要对batch_size有充分的理解。

batch_size对于优化函数的影响从某种程度上是从计算开销中体现的。

我认为计算开销是指在迭代过程中，所产生的不可避免的误差。（挖坑）

举个比较形象的例子来说明batch_size：

在秋天收农作物的时候，有直接装车和先装袋再装车的两种方式，将农作物装车视作一次迭代周期（进行了模型训练）。直接装车能联想的问题至少有两个：一是在装车的过程中会造成农作物的流失，而且会比后者装车的方式多；二是在运输的过程中，由于是散装的，也会造成一定程度上的流失。但是装载的过程很快，反观后者的方式，虽然能保证农作物的基数却在装袋上花费了更多的时间。

这也引入了一个关键的概念：模块化

深度学习中，绝大部分问题都需要进行模块化处理。

动量法

学习了上面的三种优化算法后，是否会思考一件事情——它们在实质上（即：数学原理）并没有多大的区别。那么动量法将会在此基础上做出了一些改进。

动量法跟之前的优化算法的区别在于它是为了针对多元函数中参数梯度下降的方向不同从而提供一种新的迭代方式。（关于梯度与梯度下降以后会补上），首先，先来看一下梯度下降的一些问题。

同样，让我们考虑一个二维向量，对目标函数的参数做了一些修改

eta = 0.4

def train_2d(trainer):
    x1, x2 = -5, -2
    results = [(x1, x2)]
    for i in range(20):
        x1, x2 = trainer(x1, x2)
        results.append((x1, x2))
    print(f'epoch {i+1}, x1 {x1}, x2 {x2}')
    return results

def show_trace_2d(f, results):
    d2l.set_figsize(figsize = (10, 8))
    d2l.plt.plot(*zip(*results), '-o', color = '#ff7f0e')
    # *的用法
    x1, x2, s1, s2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1),
                                0, 0)
    d2l.plt.contour(x1, x2, f(x1, x2), color = '#1f77b4')
    # contour 等高线、轮廓
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')
 
def f_2d(x1, x2):
    return (0.1 * x1 ** 2, 2 * x2 ** 2)

def g_2d(x1, x2, s1, s2):
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

show_trace(f_2d, train_2d(g_2d))

 OK，跟之前的图像比对后发现，在y轴(x2)的梯度变化十分明显，并且x2在-3左右就趋于稳定；而x轴(x1)在最开始的变化幅度相较于x2很小。如图，在图像初期，任取一点后发现，同一位置上目标函数在竖直方向(即y轴方向)比水平方向(即x轴方向)的偏导数的绝对值大的多。

水平方向上x1的迭代方式是      ， 这里的学习率不进行自我衰减。不难发现，对于x1来说，在其梯度值（0.2）较小的情况下，选择了一个较小的学习率，就会导致x1的迭代速度比较慢。

不妨把学习率从0.4调到0.6

eta = 0.6

show_trace(f_2d, trainer_2d(gd_2d))

自变量在竖直方向(x2)不断跨过最优解，逐渐发散。

在多元函数中，单一固定的学习率往往只能使自变量的一部分迭代时沿着当前位置梯度下降的最快方向。

动量法的提出就是为了解决上述的关于梯度下降问题。

沿用小批量随机梯度下降中的时间步的小批量梯度的定义。设时间步的自变量，学习率为。在时间步为0时，动量法创建了速度变量，初始值为0，并做了一下迭代

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​       ​​​​​​ 

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

当时，动量法等价于小批量随机梯度下降。

先来看一下使用动量法后，图像的走向发生的变化

def momentum_2d(x1, x2, v1, v2):
    return (x1 - v1, x2 - v2, v1, v2)

eta , gamma = 0.4, 0.5
show_trace_2d(f_2d, trainer_2d(momentum_2d))

虽然图像变得更曲折，但是水平方向，x1更快逼近了最优解

学习率为0.6时

eta = 0.6

show_trace_2d(f_2d, trainer_2d(momentum_2d))

 竖直方向也不再发散。

下面来讲解动量法的数学原理。

动量法的提出，要归结于一个数学概念：指数加权平均。

给定超参数，当前时间步t的变量是上一步的变量和当前时间步另一变量的线性组合：
        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​ 

对自变量展开不难得到一下规律：

令有

反之，有令此时

我们把当成一个比较小的数（等同高数中，“比较小的数”），可以将比含的项和比系数更高的项忽略。

将自变量归纳成 

实际应用中，经常把作为步长的加权平均。

我们回到动量法的速度变量的迭代进行一些变形：

发现跟上述的指数加权移动平均相似。

与小批量随机梯度下降不同的是，动量法的迭代不只取决于当前梯度，而是取决于前个步长中的各个梯度方向。这样，我们就可以使用较大的学习率来更快的训练模型了。

def init_momentum_states():
    v_w = nd.zeros((features.shape[1], 1))
    v_b = nd.zeros(1)
    return v_w, v_b

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        v[:] = hyperparams['momentum'] * v + hyperparams['lr'] * p.grad 
        p[:] -= v

先将动量法的超参数设置成0.5，这时，可以看作是特殊的小批量随机梯度下降：其小批量随机梯度为最近2个时间步的2倍小批量梯度的加权平均。

train_ch_more(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.5}, features, labels)

 将增大到0.9，这时依然可以看成是特殊的小批量随机梯度下降：其小批量随机梯度为最近10个时间步的10倍小批量梯度的加权平均。

train_ch_more(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.9}, features, labels)

 总结

以上四种优化算法，都十分的基础，但是其对后面更加复杂的优化算法的理解打下基础。从梯度下降、随机梯度下降、小批量随机梯度下降中，我们了解到了数据模块化的思想，以及其产生的影响。这也是优化算法所面临的问题之一。

而动量法则是为了解决一类梯度方向问题，使自变量在迭代过程中方向保持一致，实际上向量间的方向应该如图所示。若动量梯度方向与当前梯度方向相同，矢量相加则会加大梯度，若不同，则会进行修正。

优化算法仍然有许多问题可以讨论，会在以后不断推出。

如果其中有错误的地方欢迎指正！