[行人重识别论文阅读]Fine-Grained Shape-Appearance Mutual Learning for Cloth-Changing Person Re-Identification

论文地址
论文代码：暂无

文章思想

在上篇文章中我们引入了sketch（行人轮廓图）的思想去解决换衣问题，但是我们会在实践中发现sketch的优劣性严重影响了最后实验结果的好坏。此篇论文的核心思想就提高行人轮廓图的图片质量。

利用行人标签提高轮廓图质量

想法很简单就是如果该行人轮廓图能够正确的预测出行人的标签，那么其行人轮廓图的质量就会非常不错。

下述公式描述了如何提取行人的轮廓:
我们首先利用下述公式获得行人的掩码,I为输入图像,Θm为网络的参数,Fm为语义解析网络,这样我们得到的就是行人的掩码M

之后将得到M投入到Fs中得到轮廓特征, Θs为Fs的参数

虽然这种方法很好但是会出现一个问题：

如上图的(c）所示除了轮廓以外的其它细节也被引入，其它细节虽然会提高模型的预测准确率 但是我们只是想要行人的轮廓，所以我们需要对其额外处理：

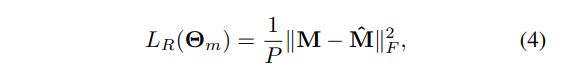
M^ 就是一开始的预训练模型，没有经过上面损失进行训练的，由于没有经过上面损失的训练，虽然他在轮廓方面不够细节与完整，但是却不会引入轮廓以外的东西。

所以我们就需要优化Fm网络，如上述公式（4）让M与M^距离距离更近即使损失函数更小来优化Fm。

姿势与行人轮廓

通过上述的方法我们得到了高质量的行人轮廓，但是无论这个轮廓有多么完美，同一个人的不同姿势轮廓肯定是不相同的，所以我们要更好的利用轮廓图就要去除姿势对轮廓图的干扰。

解决方法：同一个姿势的轮廓图用一个网络处理

如上图所示 我们首先提取人体的关键点，根据关键点我们利用聚类算法将图片分成三个组，利用聚类的结果我们为每个轮廓图添加伪标签。

有了伪标签之后，我们首先将轮廓图通过一个特征提取网络，这个网络一共有4个block，block1，block2，block3，在block4的时候，我们上面提过同一个姿势的轮廓图用同一个网络去处理，现在一共有三种姿态，所以我们分为3个block4，每个block4处理一种姿势，而轮廓图具体经过哪个block就是根据伪标签来定

那么最终的结果就是由三个block4的结果得出，值得注意的是，这个权重是对应姿势的block4为1，其余全为0，实质上就是只有一个block4的结果。

这样得到的特征向量是一个去除姿势影响，能够明确判别行人的高质量轮廓图

得到外观特征

上述我们求得的特征实际上是行人的形状特征，我们为了提高最终识别行人的准确率，我们同时引入了学习外观特征，例如学习头肩特征，步态特征等

下图红框部分即是我们求外观特征的网络

这部分就很简单了 就是利用4个block不断提取特征后加上Id损失和三元组损失，这样就能提取到与衣服无关的特征（因为数据集是换衣数据集，降低损失就是在不断提取与衣服无关的特征）

外观特征与形状特征的融合学习

为了融合两种特征的学习，我们提出了dense interactive mutual learniing

而对于这个共同学习我们提供了两种方式：

相似度矩阵的共同学习

损失函数：
公式中 Sia代表 形状分支得到的相似度矩阵
公式中 Sjs代表 外观分支得到的相似度矩阵

而我们的损失函数就是让两个矩阵更加接近（即这样就是使同一个人的形状特征和外观特征同时考虑进去，因为两者得到的相似度较近就说明两者判断的应该是一个人）

概率分布的学习

我们上文说过利用标签判断趋于一致是一种很好的方法，所以我们使用上这个思想，比较两种特征在概率分布上的一致性

下述的计算方式我们称为相对熵

它的概念：
它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布P(x)的事件空间，若用概率分布Q（x）编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用D（P||Q）表示KL距离，计算公式如下：

那么我们的目的就是让两者的概率分布更加接近（即ps与pa相互更加接近）
如下公式除了引入（10）中ps相对与pa的关系 我们又引入了pa相对于ps的关系。
这样我们发现两者的概率分布越接近，其损失函数就会越趋于0.

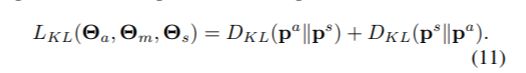
我们将两个损失函数共同运用起来就完成了我们共同学习的过程

博客参考

https://zhuanlan.zhihu.com/p/393732836
https://blog.csdn.net/scw1023/article/details/59109922