863. All Nodes Distance K in Binary Tree

Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

Example 1:

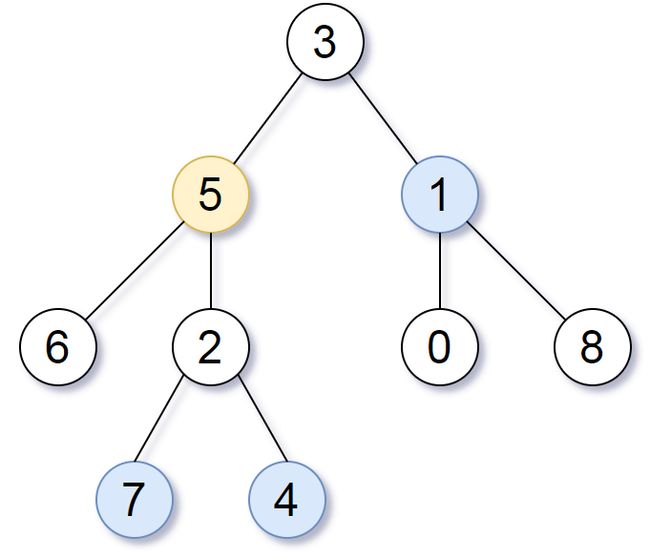
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

Example 2:

Input: root = [1], target = 1, k = 3
Output: []

Constraints:

• The number of nodes in the tree is in the range [1, 500].
• 0 <= Node.val <= 500
• All the values Node.val are unique.
• target is the value of one of the nodes in the tree.
• 0 <= k <= 1000

题目： 给定一个二叉树，和其中一个节点。求与给定节点距离为k的所有节点的值。路径不一定要过根节点。

思路：首先需要找到给定的节点位置。距离给定节点target 为k的节点可能在target之下（子孙辈节点），也可能在target之上（祖辈节点），也可能在target旁边。因此需要两种操作，一种向下寻找距离给定节点为k，一种向上寻找。向下寻找比较简单，只找到距离为k的节点并放入结果中即可。向上寻找需要逐层寻找，比如向上一层找到target的parent后，需要再找到旁支与partent距离为k-1的所有节点。再向上二层找到parent的parent……以此类推。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void getDownNode(TreeNode* node, int k, vector& res){
        if(!node || k < 0) return;
        if(k == 0){
            res.push_back(node->val);
            return;
        }
        getDownNode(node->left, k-1, res);
        getDownNode(node->right, k-1, res);
    }
    int getUpNode(TreeNode* node, TreeNode* target, int k, vector& res){
        if(!node) return -1;
        if(node == target){
            getDownNode(node, k, res);
            return 0;
        } else {
            int left = getUpNode(node->left, target, k, res);
            int right = getUpNode(node->right, target, k, res);
            if(left == -1 && right == -1) return -1;
            else if(left != -1){
                if(left == k-1) res.push_back(node->val);
                getDownNode(node->right, k-left-2, res);
                return left+1;
            } else if(right != -1){
                if(right == k-1) res.push_back(node->val);
                getDownNode(node->left, k-right-2, res);
                return right+1;
            }
        }
        return -1;
    }
    vector distanceK(TreeNode* root, TreeNode* target, int k) {
        vector res;
        getUpNode(root, target, k, res);
        return res;
    }
};