机器学习之手写决策树以及sklearn中的决策树及其可视化

决策树理论部分

决策树的思路很简单，就是从数据集中挑选一个特征，然后进行分类。

基本算法

从伪代码中可以看出，分三种情况考虑：
（1）如果输入样本同属于一类，那么将节点划分为此类的叶节点。
（2）如果属性划分次数达到上限，即属性划分完了，或者是样本中在此类属性取值都一样，可以认为全部划分仍然存在不同类的样本，那么这个节点就标记为类别数占较多的叶节点。
（3）需要继续划分的情况，选择一个属性对数据集进行划分。

划分选择

划分选择还是比较重要的，因为不同的划分选择会建出不同的决策树。划分选择的指标就是希望叶节点的数据尽可能都是属于同一类，即节点的“纯度”越来越高。

信息熵

其中|y|是指样本标签的种类的个数，p_k代表第k类样本所占的比例

信息增益

|D^v|代表a特征中同样是v值的样本的数量。
当前样本此特征的信息增益 = 当前样本的信息熵 - 加权求和的同特征值的样本的信息熵。

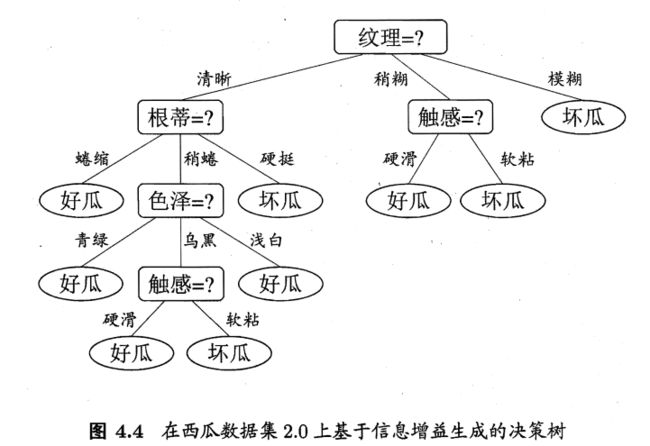
举个例子

西瓜数据集2.0如下

首先计算样本的信息熵

然后计算各个特征的信息增益


可见纹理的信息增益最大，也说明用纹理来划分当前数据，得到的纯度是最高的。

信息增益率

因为信息增益对可取值较多的属性有所偏好，为了减少这个影响，可以采用信息增益率。

但是仍然存在问题：

基尼系数

基尼指数

决策树代码实现

千言万语都在注释里了。

import math
import numpy
import numpy as np
import collections
from sklearn.model_selection import train_test_split
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier  # 导入决策树DTC包


class DecisionNode(object):
    def __init__(self, f_idx, threshold, value=None, L=None, R=None):
        self.f_idx = f_idx  # 属性的下标，表示通过下标为f_idx的属性来划分样本
        self.threshold = threshold  # 下标 `f_idx` 对应属性的阈值
        self.value = value  # 如果该节点是叶子节点，对应的是被划分到这个节点的数据的类别
        self.L = L  # 左子树
        self.R = R  # 右子树


# 寻找最优的阈值
def find_best_threshold(dataset: np.ndarray, f_idx: int, split_choice: str):  # dataset:numpy.ndarray (n,m+1) x<-[x,y]  f_idx:feature index
    best_gain = -math.inf  # 信息增益越小纯度越低
    best_gini = math.inf # 基尼值越大纯度越低
    best_threshold = None
    candidate = [0, 1]  # 因为只有01，就用这两个来划分。候选值1代表是这个特征，0代表不是这个特征

    # 遍历候选值，找出纯度最大的划分值（这里是0或者1）
    for threshold in candidate:
        L, R = split_dataset(dataset, f_idx, threshold)   # 根据阈值分割数据集，小于阈值
        gain = None
        if split_choice == "gain":
            # 计算信息增益
            gain = calculate_gain(dataset, L, R)  # 根据数据集和分割之后的数
            if gain > best_gain:  # 如果增益大于最大增益，则更换最大增益和最大阈值
                best_gain = gain
                best_threshold = threshold
        if split_choice == "gain_ratio":
            # 计算信息增益率
            gain = calculate_gain_ratio(dataset, L, R)
            if gain > best_gain:  # 如果增益大于最大增益，则更换最大增益和最大阈值
                best_gain = gain
                best_threshold = threshold
            # 计算基尼指数
        if split_choice == "gini":
            gini = calculate_gini_index(dataset, L, R)
            if gini < best_gini:  # gini指数越小越好
                best_gini = gini
                best_threshold = threshold
    # 返回此特征最优的划分值（0或1）以及对应的信息增益/增益率/基尼指数
    return best_threshold, best_gain


# 计算信息熵
def calculate_entropy(dataset: np.ndarray):  # 熵
    scale = dataset.shape[0]  # 多少条数据
    d = {}
    for data in dataset:
        # 一条数据的最后一位是标签
        key = data[-1]
        # 统计数据类别个数
        if key in d:
            d[key] += 1
        else:
            d[key] = 1

    entropy = 0.0
    for key in d.keys():
        # pk
        p = d[key] / scale
        # -pk * log2(pk)
        entropy -= p * math.log(p, 2)
    return entropy


# 计算信息增益
def calculate_gain(dataset, l, r):
    # l:左子树的数据
    # r:右子树的数据
    # 计算信息熵
    e1 = calculate_entropy(dataset)
    # 因为每个特征只有两种取值，是或不是（l,r已然是按特征分开的两类）
    e2 = len(l) / len(dataset) * calculate_entropy(l) + len(r) / len(dataset) * calculate_entropy(r)
    gain = e1 - e2
    return gain


# 计算信息增益率
def calculate_gain_ratio(dataset, l, r):
    s = 0
    gain = calculate_gain(dataset, l, r)
    p1 = len(l) / len(dataset)
    p2 = len(r) / len(dataset)
    # 会出现 1/0 的情况 全被划分到一边 s=0
    # 只有0，1两种取值
    if p1 == 0:
        s = p2 * math.log(p2, 2)
    elif p2 == 0:
        s = p1 * math.log(p1, 2)
    else:
        s = - p1 * math.log(p1, 2) - p2 * math.log(p2, 2)

    # 如果s为0，说明全都划分到一类，信息增益率可以看成无限大
    if s == 0:
        gain_ratio = math.inf
    else:
        gain_ratio = gain / s

    return gain_ratio


# 计算基尼系数（随机抽取两个样本，其类别不一致的概率）
def calculate_gini(dataset: np.ndarray):
    scale = dataset.shape[0]  # 多少条数据
    d = {}
    for data in dataset:
        key = data[-1]
        if key in d:
            d[key] += 1
        else:
            d[key] = 1

    gini = 1.0
    for key in d.keys():
        p = d[key] / scale
        gini -= p * p
    return gini


# 计算基尼指数，基尼指数越小，纯度越高
def calculate_gini_index(dataset, l, r):
    gini_index = len(l) / len(dataset) * calculate_gini(l) + len(r) / len(dataset) * calculate_gini(r)
    return gini_index


def split_dataset(X: np.ndarray, f_idx: int, threshold: float):
    # 左边是f_idx特征小于阈值的数据
    # 右边是大于阈值的数据
    L = X[:, f_idx] < threshold
    R = ~L
    return X[L], X[R]


def majority_count(dataset):
    class_list = [data[-1] for data in dataset]
    # 返回数量最多的类别
    return collections.Counter(class_list).most_common(1)[0][0]


def build_tree(dataset: np.ndarray, f_idx_list: list, split_choice: str):   # return DecisionNode 递归
    # f_idx_list 待选取特征的列表
    class_list = [data[-1] for data in dataset]  # 类别
    # 全属于同一类别（二分类）
    if class_list.count(class_list[0]) == len(class_list):
        return DecisionNode(None, None, value=class_list[0])
    # 若属性都用完, 标记为数量最多的那一类
    elif len(f_idx_list) == 0:
        value = collections.Counter(class_list).most_common(1)[0][0]
        return DecisionNode(None, None, value=value)
    else:
        # 找到划分 增益最大的属性
        best_gain = -math.inf
        best_gini = math.inf
        best_threshold = None
        best_f_idx = None

        # 遍历所有特征，找出纯度最大的那个特征
        for i in f_idx_list:
            threshold, gain = find_best_threshold(dataset, i, split_choice)
            # 基尼指数越小纯度越大
            if split_choice == "gini":
                if gain < best_gini:
                    best_gini = gain
                    best_threshold = threshold
                    best_f_idx = i
            # 信息增益/信息增益率越大，纯度越大
            if split_choice == "gain" or split_choice == "gain_ratio" :
                if gain > best_gain:  # 如果增益大于最大增益，则更换最大增益和最大
                    best_gain = gain
                    best_threshold = threshold
                    best_f_idx = i

        # 拷贝原特征
        son_f_idx_list = f_idx_list.copy()
        # 移除进行分类的特征（挑选出的最优特征）
        son_f_idx_list.remove(best_f_idx)

        # 以最优阈值分割数据
        L, R = split_dataset(dataset, best_f_idx, best_threshold)
        # 左边的数据为0那么说明已经全都为一类了，那么叶节点就产生了
        if len(L) == 0:
            L_tree = DecisionNode(f_idx=None, threshold=None, value=majority_count(dataset))  # 叶子节点
        # 否则就继续往下划分
        else:
            L_tree = build_tree(L, son_f_idx_list, split_choice)  # return DecisionNode

        # 右边也同理
        if len(R) == 0:
            R_tree = DecisionNode(f_idx=None, threshold=None, value=majority_count(dataset))  # 叶子节点
        else:
            R_tree = build_tree(R, son_f_idx_list, split_choice)  # return DecisionNode
        # 递归调用建树
        return DecisionNode(f_idx=best_f_idx, threshold=best_threshold, value=None, L=L_tree, R=R_tree)


def predict_one(model: DecisionNode, data):
    if model.value is not None:
        return model.value
    else:
        feature_one = data[model.f_idx]
        branch = None
        if feature_one >= model.threshold:
            branch = model.R  # 走右边
        else:
            branch = model.L   # 走左边
        return predict_one(branch, data)


def predict_accuracy(y_predict, y_test):
    y_predict = y_predict.tolist()
    y_test = y_test.tolist()
    count = 0
    for i in range(len(y_predict)):
        if int(y_predict[i]) == y_test[i]:
            count = count + 1
    accuracy = count / len(y_predict)
    return accuracy


class SimpleDecisionTree(object):
    def __init__(self, split_choice):
        # split_choice 分割策略：信息增益、信息增益率或者基尼指数
        self.split_choice = split_choice

    def fit(self, X: np.ndarray, y: np.ndarray):
        dataset_in = np.c_[X, y] # 纵向拼接
        f_idx_list = [i for i in range(X.shape[1])]# 特征列
        self.my_tree = build_tree(dataset_in, f_idx_list, self.split_choice) # 建树

    def predict(self, X: np.ndarray): 
        predict_list = []
        for data in X:
            predict_list.append(predict_one(self.my_tree, data))

        return np.array(predict_list)


if __name__ == "__main__":
    predict_accuracy_all = []
    import pandas as pd
    for i in range(10):
        data = pd.read_csv("data.csv")
        y = data["label"].values 
        x = data.drop(columns="label").values

        X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

        predict_accuracy_list = []  # 储存4种结果
        split_choice_list = ["gain", "gain_ratio", "gini"]
        for split_choice in split_choice_list:
            m = SimpleDecisionTree(split_choice)
            m.fit(X_train, y_train)
            y_predict = m.predict(X_test)
            y_predict_accuracy = predict_accuracy(y_predict, y_test.reshape(-1))
            predict_accuracy_list.append(y_predict_accuracy)
            
        clf = DecisionTreeClassifier()  # 所以参数均置为默认状态
        clf.fit(X_train, y_train)  # 使用训练集训练模型
        predicted = clf.predict(X_test)
        predict_accuracy_list.append(clf.score(X_test, y_test))
        predict_accuracy_all.append(predict_accuracy_list)

    p = numpy.array(predict_accuracy_all)
    p = np.round(p, decimals=3)
    accs = []
    for i in p:
        accs.append(i)
    accs = pd.DataFrame(accs)
    accs.columns = ["gain", "gain_ratio", "gini", "sklearn"]
    print(accs)

输出结果：

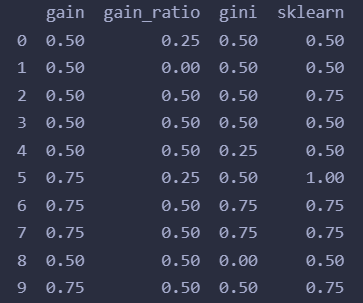
我们还可以可视化一下sklearn帮我们建立的决策树：

from sklearn import tree
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['FangSong']  # 指定中文字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

fn=data.columns[:-1]
cn=['坏瓜', '好瓜']
fig, axes = plt.subplots(nrows = 1,ncols = 1,figsize = (4,4), dpi=300)
tree.plot_tree(clf,
               feature_names = fn, 
               class_names=cn,
               filled = True);
# value表示对应类别的样例分别有多少个。

还是sklearn比较好。

参考

机器学习——周志华
手写分类决策树（鸢尾花数据集）