回溯模板（2）——解决全排列问题

CSDN话题挑战赛第2期
参赛话题：面试宝典

上回写的组合问题与回溯模板简单概述在：回溯模板——解决组合问题

就不进行回溯的介绍了，直接给出回溯算法的模板：

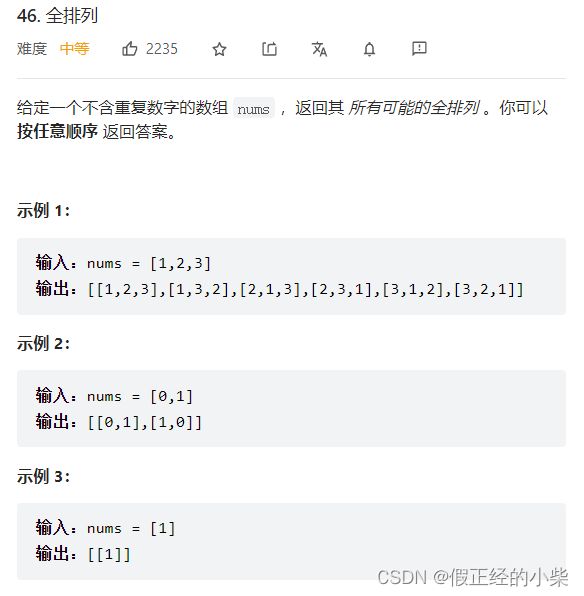
 46.全排列

什么叫全排列？

就是把给出的序列排列成不同的组合（组合的长度会和给出的序列长度相同）

题目：

 知道这是组合问题，然后可以用回溯去解后，根据步骤来：

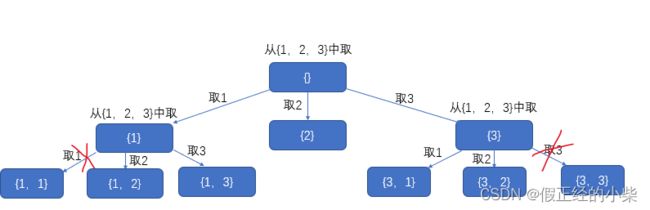
先构图使思路更清晰（还有抓住题目关键字：给出的序列里面没有重复元素）：

这里我没有画全，画了个大概：

从图中我们可以得出，我们可以一直在序列中选取元素，但不能选选取过了的，如果选过了的，也就是组合里面有了的，那我们对其进行剪枝。

如何判断有没有被选取过呢？

我们可以创建一个布尔类型的数组，由于题目给出序列里每个元素都不相同，那么元素对应的索引就可以表示那个元素，是否为true就可以表示有无被选过。

由上面这些所得的信息，我们就可以套用模板了。

代码实现：

C++版：

class Solution {
private:
    vector path;//存放排列的元素
    vector> rec;//存放符合要求的组合
    void huisuo(vector nums,bool ff[nums.size()]){
        if(path.size()==nums.size()){
            rec.push_back(path);
            return;
        }
        for(int i=0;i> permute(vector& nums) {
        bool ff[nums.size()];
        //给判断元素是否访问的数组进行初始化
        for(int i=0;i

Java版：

public class Solution {

    public List> permute(int[] nums) {
        int len = nums.length;
        // 使用一个动态数组保存所有可能的全排列
        List> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        boolean[] used = new boolean[len];
        List path = new ArrayList<>();

        dfs(nums, len, 0, path, used, res);
        return res;
    }

    private void dfs(int[] nums, int len, int depth,
                     List path, boolean[] used,
                     List> res) {
        if (depth == len) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 在非叶子结点处，产生不同的分支，这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。
        for (int i = 0; i < len; i++) {
            if (!used[i]) {
                path.add(nums[i]);
                used[i] = true;

                dfs(nums, len, depth + 1, path, used, res);
                // 注意：下面这两行代码发生 「回溯」，回溯发生在从 深层结点 回到 浅层结点 的过程，代码在形式上和递归之前是对称的
                used[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }
}

（Java版这里得注意path这里定义的是引用类型变量，它里面存的东西是在变的，所以当我们存入的时候得对它进行拷贝，new新的对象存进去，否则的话rec“容器”里面会全是空的）

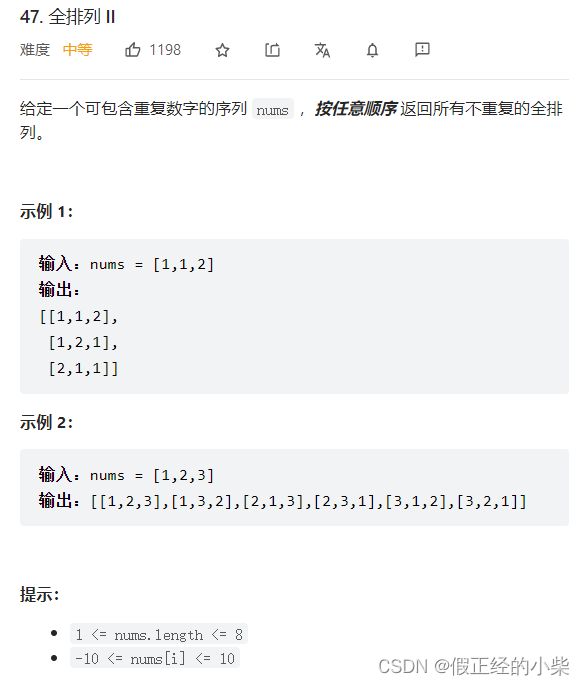
47.全排列 ||

题目：

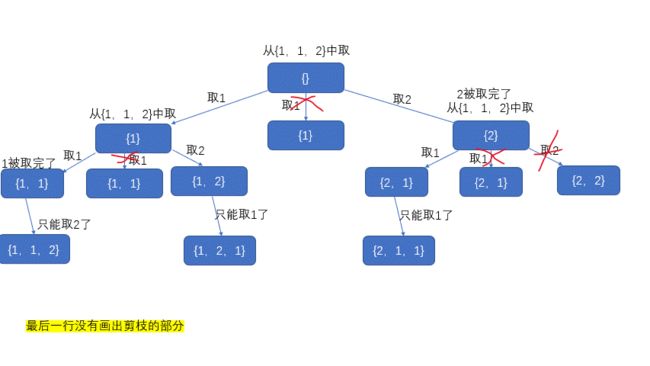
画图：

 分析所画图进行剪枝的地方：1.树同一深度的节点数据不能一致，应剪枝（以该数字为这个位置的全排列都会在树的后续节点中出现，如果树同一深度有俩一样的数据那将出现俩种一样的排列，重复了我们对其进行剪枝）

剪枝方法：先对序列进行个排序（可以让相同的元素是相邻的），用个if语句判断插入的元素不与前一个元素相同，这样可以使插入同一深度的节点里保持不同数据

2. 如果序列元素已经取完了，不能再取了，进行剪枝。（比如取了一个2，序列里面没2了，那树的下一次节点里就不会再取2了，因为没了）

剪枝方法：用哈希表对序列元素个数进行统计，如果为0的话进行剪枝，不可以再插入了。

思路了解完后，开始套模板了：

C++版：

class Solution {
private:
        vector path;
        vector> rec;
        void huisuo(vector nums,map mp){
            //存放结果
            if(path.size()==nums.size()){
                rec.push_back(path);
            }
            for(int i=0;i0&&nums[i]==nums[i-1])
                continue;
                if(mp[nums[i]]==0)
                continue;
                //处理节点
                --mp[nums[i]];
                path.push_back(nums[i]);

                huisuo(nums,mp);
                //回溯
                ++mp[nums[i]];
                path.pop_back();
            }
        }
public:
    vector> permuteUnique(vector& nums) {
        //先给数组排个序
        sort(nums.begin(),nums.end());
        //定义个哈希表统计序列元素个数
        map mp;
        for(int x:nums){
            mp[x]++;
        }
        huisuo(nums,mp);
        return rec;
    }
};

Java版：

class Solution {
    private List path = new ArrayList<>();
    private List> rec = new ArrayList<>();
    public List> permuteUnique(int[] nums) {
        //先进行个排序
        Arrays.sort(nums);
        //定义哈希表，统计序列里各个元素的数目
        HashMap mp = new HashMap();
        for(int x:nums){
            if(mp.get(x)==null)
            mp.put(x,1);
            else
            mp.put(x,mp.get(x)+1);
        }
        huisuo(nums,mp);
        return rec;
    }
    private void huisuo(int[] nums,HashMap mp){
        if(path.size()==nums.length){
            rec.add(new ArrayList<>(path));
            return;
        }
        for(int i=0;i0&&nums[i]==nums[i-1])
            continue;
            //该数已经用光了，不能组成排列了
            if(mp.get(nums[i])==0)
            continue;
            mp.put(nums[i],mp.get(nums[i])-1);//对使用过的数，数目进行减1
            path.add(nums[i]);

            huisuo(nums,mp);
            //回溯
            mp.put(nums[i],mp.get(nums[i])+1);
            path.remove(path.size()-1);
        }
    }
}

（再提一下：回溯是可以解决与组合有关的问题，但它并不是最优算法（属于暴力解法，如果不带剪枝的话），想优化复杂度，可以去思考更好的解题算法）