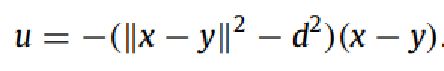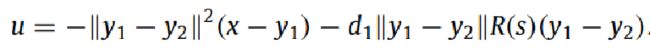无人机编队算法(Target-point formation control)
基于目标点的编队控制:参考论文:
https://www.sciencedirect.com/science/article/pii/S0005109815003234
摘要:
本文提出了一种新的分布式反馈策略来控制平面上运动点模型运动,形成刚性无环的编队。该方法利用了“目标点”的概念,它的底层有向图可以由一系列Henneberg顶点加法生成,适用于任何二维的编队。结果表明,如果指定领航者和第一个跟随者在不同的位置开始,该方法可以使一组在平面上任意给定初始位置开始的多个运动点以指数速度进入期望的编队。
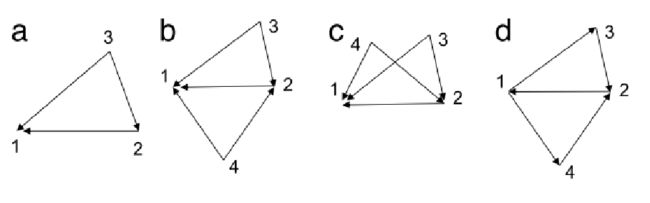
1 最小刚性定向编队
Agent2跟踪agent1,自agent3之后开始选择之前的两个agent进行跟踪,形成的编队称为vertex-addition formations 上图中d不符合。
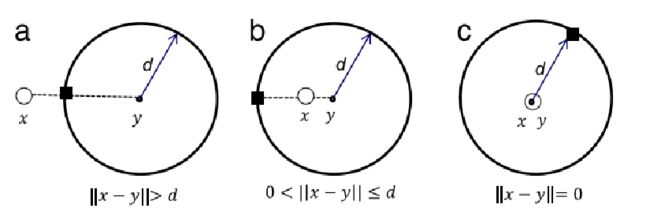
2 一个领航者
目标点位置:
其中,y是领航者的位置,x是第一跟随者的位置,![]() 是目标点的位置,根据领航者和跟随着确定目标点的位置,跟随着只需要去跟随目标点的位置即可。
是目标点的位置,根据领航者和跟随着确定目标点的位置,跟随着只需要去跟随目标点的位置即可。
控制律设计:
解释:如果你能理解PID控制, u是控制量<输入量>,可以把它理解成一个可变参的P控制,x-y是当前位置和期望位置的差,前面那个是比例系数,只不过比例系数随着当前距离与期望距离而变化
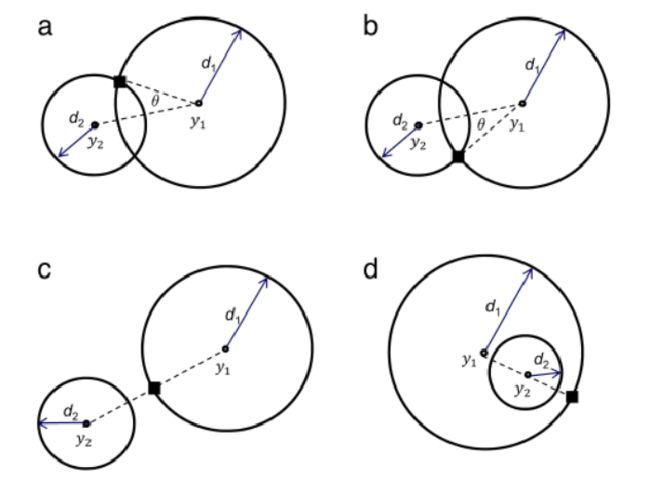
3 两个领航者
确定目标点的位置:两个领航者包括四种情况,除了cd两种特殊情况以外,可以注意到,ab也包括了两种情景,也就是说如果跟随者与第一领航者的距离为d1,与第二领航者的距离为d2,其实,跟随者的位置并不是唯一确定的。
为了确定跟随者的位置,引入顺逆时针的概念
控制律的设计:
仿真实现效果:
话不多说,直接附上复现的Matlab代码:
clc;clear;close;
global y1 y2 d1 d2
n = 3000;
dis21=zeros(n,1);
dis31=zeros(n,1);
dis32=zeros(n,1);
dis41=zeros(n,1);
dis42=zeros(n,1);
v1=zeros(n,2);
v2=zeros(n,2);
v3=zeros(n,2);
v4=zeros(n,2);
p1=zeros(n,2);
p2=zeros(n,2);
p3=zeros(n,2);
p4=zeros(n,2);
%p1 p2 p3 p4 是四者坐标 v1 v2 v3 v4是四者速度
%位置初始化
p1(1,:)=[0,0];
p2(1,:)=[10,0];
p3(1,:)=[3,4];
p4(1,:)=[0,4];
figure(1);
%速度初始化
v1(1,:)=[0,0];
v2(1,:)=[0,0];
v3(1,:)=[0,0];
v4(1,:)=[0,0];
dt=0.001;
%目标距离
d21=3;
d31=4;
d32=5;
d41=5;
d42=4;
%顺时针为1 逆时针为-1
gama3=-1;
gama4=1;
pic_num=1;
for i = 1:n
t=dt*(i-1);%时间积累
%% 距离计算
dis21(i)=cal_pp(p1(i,:),p2(i,:));%计算21距离
dis31(i)=cal_pp(p3(i,:),p1(i,:));%计算31距离
dis32(i)=cal_pp(p3(i,:),p2(i,:));%计算32距离
dis41(i)=cal_pp(p1(i,:),p4(i,:));%计算21距离
dis42(i)=cal_pp(p4(i,:),p2(i,:));%计算31距离
%% V1速度更新
v1=[0,exp(-t)];%1速度更新
%% V2速度更新
v2=-(dis21(i)^2-d21^2)*(p2(i,:)-p1(i,:));%v2速度更新
%% V3速度更新
transforming(d32,d31,p2(i,:),p1(i,:),p3(i,:));
s3=cal_s(y1,y2,d1,d2);
Rs3=[s3,gama3*sqrt(1-s3^2);-gama3*sqrt(1-s3^2),s3];
v3=-dis21(i)^2*(p3(i,:)-y1)'-d1*dis21(i)*Rs3*(y1-y2)';%v3速度更新
%% V4速度更新
transforming(d42,d41,p2(i,:),p1(i,:),p4(i,:));
s4=cal_s(y1,y2,d1,d2);
Rs4=[s4,gama4*sqrt(1-s4^2);-gama4*sqrt(1-s4^2),s4];
v4=-dis21(i)^2*(p4(i,:)-y1)'-d1*dis21(i)*Rs4*(y1-y2)';%v4速度更新
%% 位置更新
p1(i+1,1)=p1(i,1)+v1(1)*dt ;%1位置更新
p1(i+1,2)=p1(i,2)+v1(2)*dt ;
p2(i+1,1)=p2(i,1)+v2(1)*dt ;%2位置更新
p2(i+1,2)=p2(i,2)+v2(2)*dt ;
p3(i+1,1)=p3(i,1)+v3(1)*dt ;%1位置更新
p3(i+1,2)=p3(i,2)+v3(2)*dt ;
p4(i+1,1)=p4(i,1)+v4(1)*dt ;%4位置更新
p4(i+1,2)=p4(i,2)+v4(2)*dt ;
fprintf('%d\n',i);
%% 动图
if((mod(i,1)==0&&(i<20))||(mod(i,5)==0&&(i>20)&&i<100)||(mod(i,10)==0&&(i>100)&&i<200)||(mod(i,50)==0&&(i>200)))
plot(p2(i,1),p2(i,2),'c.','markersize',30);
hold on;
plot(p3(i,1),p3(i,2),'m.','markersize',30);
plot(p4(i,1),p4(i,2),'g.','markersize',30);
plot(p1(i,1),p1(i,2),'r.','markersize',30);
plot([p3(i,1),p2(i,1)],[p3(i,2),p2(i,2)],'b-','linewidth',1.5);
plot([p3(i,1),p1(i,1)],[p3(i,2),p1(i,2)],'b-','linewidth',1.5);
plot([p4(i,1),p2(i,1)],[p4(i,2),p2(i,2)],'b-','linewidth',1.5);
plot([p4(i,1),p1(i,1)],[p4(i,2),p1(i,2)],'b-','linewidth',1.5);
plot([p1(i,1),p2(i,1)],[p1(i,2),p2(i,2)],'b-','linewidth',1.5);
grid on;
text(p1(i,1)-1.5,p1(i,2),['Agent 1']);
text(p2(i,1)+0.3,p2(i,2),['Agent 2']);
text(p3(i,1)+0.3,p3(i,2),['Agent 3']);
text(p4(i,1)+0.3,p4(i,2),['Agent 4']);
xlim([-2,11]);
ylim([-5,6]);
grid on;
hold off;
F=getframe(gcf);
I=frame2im(F);
[I,map]=rgb2ind(I,256);
if pic_num == 1
imwrite(I,map,'D:\file\桌面\test.gif','gif', 'Loopcount',inf,'DelayTime',0.2);
else
imwrite(I,map,'D:\file\桌面\test.gif','gif','WriteMode','append','DelayTime',0.2);
end
pic_num = pic_num + 1;
hold off;
end
end
figure(2)
subplot(321)
t=0:dt:dt*(n-1);
plot(t,dis21,'b','linewidth',1.5);
grid on;
title('Agent2与Agent1的距离');
xlabel('时间(s)');
ylabel('距离(m)');
subplot(322)
plot(t,dis31,'b','linewidth',1.5);
grid on;
title('Agent3与Agent1的距离');
xlabel('时间(s)');
ylabel('距离(m)');
subplot(323)
plot(t,dis32,'b','linewidth',1.5);
grid on;
title('Agent3与Agent2的距离');
xlabel('时间(s)');
ylabel('距离(m)');
subplot(324)
plot(t,dis42,'b','linewidth',1.5);
grid on;
title('Agent4与Agent2的距离');
xlabel('时间(s)');
ylabel('距离(m)');
subplot(313)
plot(t,dis41,'b','linewidth',1.5);
grid on;
title('Agent4与Agent1的距离');
xlabel('时间(s)');
ylabel('距离(m)');
figure(3)
plot(p1(:,1),p1(:,2),'c*','markersize',5);
hold on;
grid on;
plot(p2(:,1),p2(:,2),'b*','markersize',5);
plot(p3(:,1),p3(:,2),'m*','markersize',5);
plot(p4(:,1),p4(:,2),'g*','markersize',5);
xlim([-2,11]);
ylim([-5,6]);
title('轨迹图');
legend('Agent1','Agent 2','Agent 3','Agent 4');
text(p1(1,1)-0.5,p1(1,2)-0.3,['1起始点']);
text(p2(1,1)+0.3,p2(1,2),['2起始点']);
text(p3(1,1)-0.5,p3(1,2)+0.3,['3起始点']);
text(p4(1,1)-1,p4(1,2)+0.5,['4起始点']);总结:
基于目标点的编队控制算法,无人机的模型为一阶模型,根据跟随者与领航者的位置差进行编队控制,方便在实物上实现(ROS)。
但是无人机之间并没有实现一致性,也就是没有位置差就无法进行控制,关于一致性的理论,可以了解这篇博客
无人机编队控制算法(基于一致性理论的编队控制)
复现完整代码:
基于目标点的编队控制MATLAB仿真-其它文档类资源-CSDN下载
使用方法把GIF文件的路径改为文件夹路径中的test.gif路径就可以了
注意:如果出现乱码,是因为matlab高版本兼容低版本,本人用的是matlab2020,建议您使用2020及更高的版本,如果是低版本,可以先用记事本打开,再复制到matlab