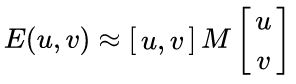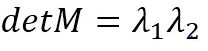harris角点检测原理
目录
1、角点概述
2、数学知识
3、Harris角点检测基本原理
4、优化改进
1、角点概述
如果一个点在任意方向的一个微小变动都会引起灰度很大的变化,那么我们就把它称之为角点,也就是一阶导数(即灰度图的梯度)中的局部最大所对应的像素点就是角点。在现实世界中,角点对应于物体的拐角,道路的十字路口、丁字路口等。基于图像灰度的方法通过计算点的曲率及梯度来检测角点。
2、数学知识
1)泰勒展开
泰勒展开公式是一种统一的形式,非常完美。
一维泰勒展开公式:
二维泰勒展开公式:
2)矩阵的特征值和特征向量
harris边角(兴趣点)检测算法 - 知乎
3、Harris角点检测基本原理
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内就不存在角点;如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。
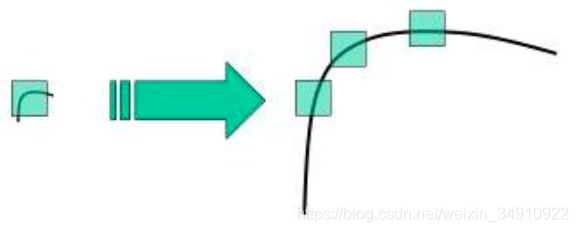
Harris 检测器具有旋转不变性,但不具有尺度不变性,也就是说尺度变化可能会导致角点变为边缘,如下图所示:
想要尺度不变特性的话,可以关注SIFT特征。
Harris 角点检测算法分为以下三步:
1、当窗口同时向 x 和 y 两个方向移动时,计算窗口内部的像素值变化量E(u,v);
2、对于每个窗口,都计算其对应的一个角点响应函数R;
3、然后对该函数进行阈值处理,如果R > threshold,表示该窗口对应一个角点特征。
E(u,v)推导过程:
首先,将图像窗口平移[u,v]产生灰度变化的自相关函数如下:
其中窗口函数(权重矩阵)可以是平坦的,也可以是高斯的,是一个二维的滤波器。对于一个角点来说, E(u,v)会非常大。因此,我们可以最大化上面这个函数来得到图像中的角点。用上面的函数计算会非常慢。因此,我们使用泰勒展开式(只有一阶)来得到这个公式的近似形式。
将平移后的式子进行泰勒展开如下:
其中Ix和Iy是I的偏微分,在图像中就是在x和y方向的梯度图(可以通过cv2.Sobel()来得到):
接下来继续推导:
把u和v拿出来,得到最终的形式:
其中矩阵M为:
最后是把实对称矩阵对角化处理后的结果,可以把R看成旋转因子,其不影响两个正交方向的变化分量。经对角化处理后,将两个正交方向的变化分量提取出来,就是 λ1 和 λ2(特征值)。
对于图像的每一个像素点(x,y),对应一个以该像素为中心的窗口w(x,y),然后该像素平移(u,v)得到新的像素点(x+u,y+v),而E(u,v)就是窗口中所有像素的加权和乘以不同位置像素的灰度差值。
矩阵M又称为Harris矩阵。w(x,y)的宽度决定了在像素x 周围的感兴趣区域。
计算响应函数R:
得到E(u,v)的最终形式,我们的目的是要找到会引起较大的灰度值变化的那些窗口。灰度值变化的大小则取决于矩阵M,那么如何找到这些窗口,我们可以使用矩阵的特征值来实现。
忽略余项之后的表达式为一个二项式函数,然而二项式函数的本质上就是一个椭圆函数,椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的,椭圆的方向是由M(x,y)的特征矢量决定的,如下图所示,椭圆方程为:
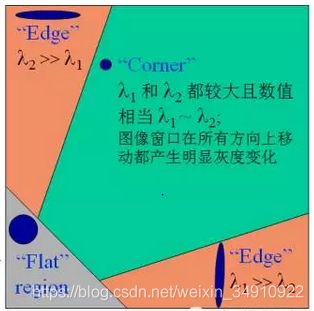
椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:
a)图像中的直线。一个特征值大,另一个特征值小,λ1>λ2或λ2>λ1。自相关函数值在某一方向上大,在其他方向上小。
b)图像中的平面。两个特征值都小,且近似相等;自相关函数数值在各个方向上都小。
c)图像中的角点。两个特征值都大,且近似相等,自相关函数在所有方向都增大。
通过M的两个特征值λ1和λ2的大小对图像点进行分类:
如果λ1和λ2都很小,图像窗口在所有方向上移动都无明显灰度变化。由于我们是通过M的两个特征值的大小对图像进行分类,所以,定义角点相应函数R:
其中k为经验常数,一般取k=0.04~0.06。为了去除加权常数κ,我们通常使用商数detM/(traceM)2作为指示器。所以,上图可以转化为:
因为特征值λ1和λ2决定了R的值,R 只与M的特征值有关,所以我们可以用特征值来决定一个窗口是平面、边缘还是角点。
平面:该窗口在平坦区域上滑动,窗口内的灰度值基本不会发生变化,所以|R|值非常小,在水平和竖直方向的变化量均较小,即Ix和Iy都较小,那么λ1和λ2都较小;
边缘:R值为负数,仅在水平或竖直方向有较大的变化量,即Ix和Iy只有一个较大,也就是λ1>>λ2或λ2>>λ1;
角点:R值很大,在水平、竖直两个方向上变化均较大的点,即Ix和Iy都较大,也就是λ1和λ2都很大。
最优角点判别:
根据R的值,将这个窗口所在的区域划分为平面、边缘或角点。为了得到最优的角点,我们还可以使用非极大值抑制。
Harris角点检测的结果是带有这些分数R的灰度图像,设定一个阈值,R > threshold,分数大于这个阈值的像素就对应角点。
4、优化改进
1)由于Harris角点检测算法的稳定性和k值有关,而k是个经验值,不好设定最佳值。
Shi-Tomasi发现,角点的稳定性其实和矩阵M的较小特征值有关,于是直接用较小的那个特征值作为分数。这样就不用调整k值了。
所以Shi-Tomasi将分数公式改为如下形式:
和Harris一样,如果该分数大于设定的阈值,我们就认为它是一个角点。
2)Harris和Shi-Tomasi都是基于梯度计算的角点检测方法,Shi-Tomasi的效果要好一些。基于梯度的检测方法有一些缺点: 计算复杂度高,图像中的噪声可以阻碍梯度计算。
想要提高检测速度的话,可以考虑基于模板的方法:FAST角点检测算法。该算法原理比较简单,但实时性很强。
3)Harris 检测器具有旋转不变性,但不具有尺度不变性,也就是说尺度变化可能会导致角点变为边缘,如下图所示:
想要尺度不变特性的话,可以关注SIFT特征。
相关链接:
1、harris角点检测算法实现
2、SHI-TOMASI角点检测