Harris角点检测原理简介+程序
Harris角点检测原理简介+程序
- Harris角点检测基本原理
-
- 基本概念
- 检测步骤
-
- 第一步:计算窗口内部的像素值变化量
- 第二步:计算角点响应函数
- 第三步:判断角点
- Harris角点检测程序
-
- python版(sobel算子)
- matlab版
- 资料
自己的理解,如有疏漏,敬请指正。
Harris角点检测基本原理
目的:寻找图像中像素值变化较大的点。
基本概念
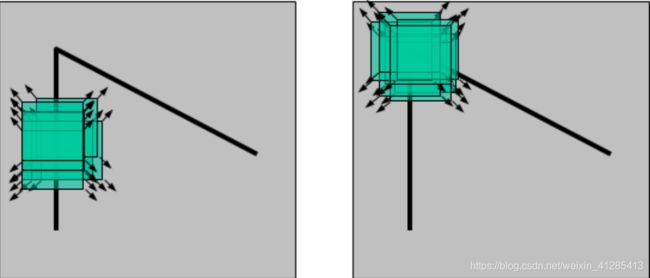
- 角点: 想象用一个滑动窗口在图像上面前后左右移动,在不均匀的区域,窗口中像素值都会发生很大变化。
- 角点和边缘的区别: 角点是无论窗口向哪个方向移动(左右/前后),像素值都会发生很大变化。而边缘是只有一个方向的像素值会发生变化。
检测步骤
角点检测基本思路:
简单来说,就是用滑动窗口在图像上移动,计算窗口内的像素值变化,据此计算角点响应函数。如果某个窗口的响应函数值大于阈值,则认为这个窗口存在角点。
第一步:计算窗口内部的像素值变化量
将图像窗口平移 [ u , v ] [u,v] [u,v] 产生的灰度值变化 E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u,v)=\sum_{x,y} w(x,y)[I(x+u,y+v)-I(x,y)]^2 E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
其中, ( x , y ) (x,y) (x,y)为窗口移动的起始中心位置, I ( x , y ) I(x,y) I(x,y)为这个位置的灰度值。窗口分别向 x x x 和 y y y 方向移动 u u u和 v v v个像素, ( x + u , y + v ) (x+u,y+v) (x+u,y+v) 为新的中心点位置, I ( x + u , y + v ) I(x+u,y+v) I(x+u,y+v) 就是这个位置的灰度值。
w ( x , y ) w(x,y) w(x,y)为位置 ( x , y ) (x,y) (x,y)处的窗口函数,表示窗口内各像素的权重。常见的窗口函数有均值、高斯等。
公式的简化推导
原理:二元函数泰勒展开
f ( x + u , y + v ) ≈ f ( u , v ) + u f x ( x , y ) + v f y ( x , y ) f(x+u,y+v)\approx f(u,v)+uf_x(x,y)+vf_y(x,y) f(x+u,y+v)≈f(u,v)+ufx(x,y)+vfy(x,y)
因此,对公式 E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u,v)=\sum_{x,y} w(x,y)[I(x+u,y+v)-I(x,y)]^2 E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2中的 [ I ( x + u , y + v ) − I ( x , y ) ] 2 [I(x+u,y+v)-I(x,y)]^2 [I(x+u,y+v)−I(x,y)]2 可以化简:
[ I ( x + u , y + v ) − I ( x , y ) ] 2 ≈ [ I ( x , y ) + u I x + v I y − I ( x , y ) ] 2 = [ u I x + v I y ] 2 = u 2 I x 2 + 2 u I x v I y + v 2 I y 2 [I(x+u,y+v)-I(x,y)]^2\\ \approx [I(x,y)+uI_x+vI_y-I(x,y)]^2\\ =[uI_x+vI_y]^2\\ =u^2I_x^2+2uI_xvI_y+v^2I_y^2 [I(x+u,y+v)−I(x,y)]2≈[I(x,y)+uIx+vIy−I(x,y)]2=[uIx+vIy]2=u2Ix2+2uIxvIy+v2Iy2
其中 I x I_x Ix和 I y I_y Iy是 I I I的微分(偏导),在图像中就是求 x x x 和 y y y 方向的梯度:
I x = ∂ I ( x , y ) ∂ x I_x=\frac{\partial I(x,y)}{\partial x} Ix=∂x∂I(x,y), I y = ∂ I ( x , y ) ∂ y I_y=\frac{\partial I(x,y)}{\partial y} Iy=∂y∂I(x,y)
代入 E ( u , v ) E(u,v) E(u,v)可得:
E ( u , v ) = ∑ x , y w ( x , y ) ( u 2 I x 2 + 2 u v I x I y + v 2 I y 2 ) = [ u v ] ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] [ u v ] = [ u v ] M [ u v ] E(u,v)=\sum_{x,y} w(x,y)(u^2I_x^2+2uvI_xI_y+v^2I_y^2)\\ =\begin{bmatrix} u&v \end{bmatrix}\quad \sum_{x,y} w(x,y)\begin{bmatrix} I_x^2& I_xI_y\\ I_xI_y& I_y^2 \end{bmatrix}\quad \begin{bmatrix} u\\v \end{bmatrix}\quad\\ =\begin{bmatrix} u&v \end{bmatrix}\quad M \begin{bmatrix} u\\v \end{bmatrix}\quad E(u,v)=x,y∑w(x,y)(u2Ix2+2uvIxIy+v2Iy2)=[uv]x,y∑w(x,y)[Ix2IxIyIxIyIy2][uv]=[uv]M[uv]
其中, M = ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] M=\sum_{x,y} w(x,y)\begin{bmatrix} I_x^2& I_xI_y\\ I_xI_y& I_y^2 \end{bmatrix}\quad M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]是实对称矩阵,可以进行对角化,表示为 M → Q − 1 [ λ 1 0 0 λ 2 ] Q M\to Q^{-1} \begin{bmatrix} \lambda_1&0\\ 0& \lambda_2\end{bmatrix}\quad Q M→Q−1[λ100λ2]Q
λ 1 , λ 2 \lambda_1, \lambda_2 λ1,λ2是矩阵特征值,Q是特征向量组成的矩阵。可以把Q看成旋转因子,不影响两个正交方向的变化分量。
第二步:计算角点响应函数
每个窗口对应的角点响应函数 R = d e t ( M ) − k ( t r a c e ( M ) ) 2 R=det(M)-k(trace(M))^2 R=det(M)−k(trace(M))2
其中 d e t ( M ) = λ 1 λ 2 det(M)=\lambda_1\lambda_2 det(M)=λ1λ2 , t r a c e ( M ) = λ 1 + λ 2 trace(M)=\lambda_1+\lambda_2 trace(M)=λ1+λ2, k k k是一个经验常数,在范围 (0.04, 0.06) 之间。
(从第一步的分析 E ( u , v ) E(u,v) E(u,v),到这里推导后,其实只要判断 M M M的特征值大小,就可以来寻找角点)
第三步:判断角点
算法的核心就是这个角点响应函数,构造得恰到好处,能够满足:
角点的 ∣ R ∣ |R| ∣R∣很大,平坦的区域 ∣ R ∣ |R| ∣R∣很小,边缘的 ∣ R ∣ |R| ∣R∣为负值
- 平坦区域: 窗口区域内的灰度值基本不会发生变化,像素点的梯度幅值非常小,即 I x I_x Ix和 I y I_y Iy都较小,此时矩阵M的两个特征值比较小,因此 ∣ R ∣ |R| ∣R∣很小;
- 边缘区域: 边缘上的像素点在x或y某个方向的梯度幅值变化比较明显,另一个方向上的梯度幅值变化较小,M两个特征值一般是一个比较大,一个比较小(当然有特殊情况,比如45°的边缘,计算出的特征值并不是都特别的大,总之跟含有角点的分布情况还是不同的),因此 ∣ R ∣ |R| ∣R∣一般为负值;
- 角点: 窗口区域内的灰度值变化非常大,M两个特征值都很大,因此 ∣ R ∣ |R| ∣R∣很大。
Harris角点检测程序
python版(sobel算子)
#角点检测
import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np
image = cv.imread('Star.jpg') #读取图像
# 输出图像尺寸
print(image.shape)
height = image.shape[0]
width = image.shape[1]
channels = image.shape[2]
print("width: %s height: %s channels: %s" % (width, height, channels))
gray_img = cv.cvtColor(image, cv.COLOR_BGR2GRAY) #cv2.COLOR_BGR2GRAY 将BGR格式转换成灰度图片
# 将数据类型转化为float32
gray_img = np.float32(gray_img)
# 检测参数设置
block_size = 3 #滑动窗口的尺寸
sobel_size = 3 #用于计算梯度图的Sobel算子的尺寸
k = 0.06 #参数k,取值范围在0.04~0.06之间
# 输入灰度图(float32)及参数,计算角点响应函数
corners_img = cv.cornerHarris(gray_img, block_size, sobel_size, k)
# 放大结果来标注角点, not necessary
kernel = cv.getStructuringElement(cv.MORPH_RECT, (3, 3))
'''这个函数的第一个参数表示内核的形状,有三种形状可以选择。
矩形:MORPH_RECT;
十字形:MORPH_CROSS;
椭圆形:MORPH_ELLIPSE;
第二和第三个参数分别是内核的尺寸以及锚点的位置。
这里表示得到一个3*3的矩形
'''
dst = cv.dilate(corners_img, kernel) #对圈圈进行膨胀操作
# Threshold for an optimal value, marking the corners in Green
# image[corners_img>0.01*corners_img.max()] = [0,0,255]
for r in range(height):
for c in range(width):
pix = dst[r, c]
if pix > 0.05 * dst.max():
cv.circle(image, (c, r), 5, (0, 0, 255), 0)
image1 = cv.cvtColor(image, cv.COLOR_BGR2RGB)
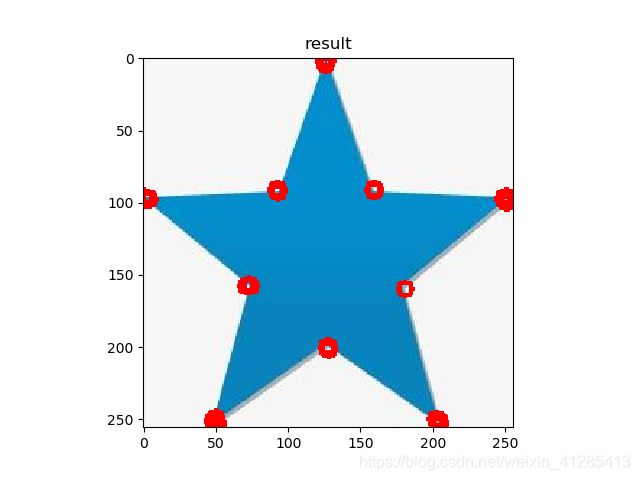
plt.imshow(image1)
plt.title("result")
plt.show()
matlab版
% 功能:检测图像harris角点
% in_image-待检测的rgb图像数组
% a--角点参数响应,取值范围:0.04~0.06
% [posr,posc]-角点坐标
in_image=imread('Star.jpg');
in_image=rgb2gray(in_image);
I=double(in_image);
%%%%计算xy方向梯度%%%%%
fx=[-1,0,1];%x方向梯度模板
Ix=filter2(fx,I);%x方向滤波
fy=[-1;0;1];%y方向梯度模板(注意是分号)
Iy=filter2(fy,I);
%%%%计算两个方向梯度的乘积%%%%%
Ix2=Ix.^2;
Iy2=Iy.^2;
Ixy=Ix.*Iy;
%%%%使用高斯加权函数对梯度乘积进行加权%%%%
%产生一个7*7的高斯窗函数,sigma值为2
h=fspecial('gaussian',[7,7],2);
IX2=filter2(h,Ix2);
IY2=filter2(h,Iy2);
IXY=filter2(h,Ixy);
%%%%%计算每个像元的Harris响应值%%%%%
[height,width]=size(I);
R=zeros(height,width);
%像素(i,j)处的响应值
for i=1:height
for j=1:width
M=[IX2(i,j) IXY(i,j);IXY(i,j) IY2(i,j)];
R(i,j)=det(M)-0.06*(trace(M))^2;
end
end
%%%%%角点判断%%%%%
Rmax=max(max(R));
%阈值
t=0.05*Rmax;
for i=1:height
for j=1:width
if R(i,j)<t
R(i,j)=0;
end
end
end
%%%%%进行3*3领域非极大值抑制%%%%%%%%%
corner_peaks=imregionalmax(R);
%imregionalmax对二维图片,采用8领域(默认,也可指定)查找极值,三维图片采用26领域
%极值置为1,其余置为0
num=sum(sum(corner_peaks));
%%%%%%显示所提取的Harris角点%%%%
[posr,posc]=find(corner_peaks==1);
figure;
imshow(in_image);
hold on
for i=1:length(posr)
plot(posc(i),posr(i),'ro');
end
边缘区域存在误差
这是由于进行角点判断时阈值偏高。将程序中t=0.06*Rmax改成t=0.02*Rmax,则效果变好:

资料
Datawhale计算机视觉基础:图像处理(下)