最强损失函数分析:一般自适应鲁棒损失函数
作者|| cocoon
编辑||3D视觉开发者社区
✨如果觉得文章内容不错,别忘了三连支持下哦~
文章目录
- 概述
-
- 广义损失函数
- 概率密度函数
- 实验
-
- 变分自编码器
- 无监督的单目深度估计
- 快速全局配准任务
- 鲁棒连续聚类任务
- 结论
- 参考文献

论文链接: https://openaccess.thecvf.com/content_CVPR_2019/papers/Barron_A_General_and_Adaptive_Robust_Loss_Function_CVPR_2019_paper.pdf
代码链接: https://github.com/jonbarron/robust_loss_pytorch
概述
文章给出了Cauchy/Lorentzian、Geman-McClure、Welsch/Leclerc、generalized Charbonnier、generalized Charbonnier、Charbonnier/pseudo-Huber/L1-L2以及L2损失函数的广义损失函数形式,在一定程度上具备着巧妙的数学美感。该损失函数可以将"鲁棒性"视作连续变量,进而强化损失函数在网络训练收敛时的鲁棒性。作为使用者,可以人工设定参数,而通过设定不同的参数,该广义损失函数又可与许多传统损失形成等价关系。
尽管参数可以人工设定,该文提出的广义损失函数还可以将鲁棒性参数作为一个训练中的自由变量,进而可以直接使用优化器进行优化,而无需人工调参。实验发现,这种“自适应”的优势在多变量输出的任务中尤为有效,比如说深度估计任务,影像生成任务等。
广义损失函数
最简单的广义损失函数可以表示为:
f ( x , α , c ) = ∣ α − 2 ∣ α ( ( ( x / c ) 2 ∣ α − 2 ∣ + 1 ) α / 2 − 1 ) f(x, \alpha, c)=\frac{|\alpha-2|}{\alpha}\left(\left(\frac{(x / c)^{2}}{|\alpha-2|}+1\right)^{\alpha / 2}-1\right) f(x,α,c)=α∣α−2∣((∣α−2∣(x/c)2+1)α/2−1)
其中, α ∈ R \alpha \in \mathbb{R} α∈R是控制鲁棒性的变形参数, c > 0 c>0 c>0是用于控制二次函数碗底有多宽的尺度系数。
当 α = 2 \alpha = 2 α=2时,该广义函数没有定义,但其非常接近 L 2 L2 L2损失:
lim α → 2 f ( x , α , c ) = 1 2 ( x / c ) 2 \lim _{\alpha \rightarrow 2} f(x, \alpha, c)=\frac{1}{2}(x / c)^{2} α→2limf(x,α,c)=21(x/c)2
当 α = 1 \alpha =1 α=1时,广义损失函数则具象为L1的平滑形式:
f ( x , 1 , c ) = ( x / c ) 2 + 1 − 1 f(x, 1, c)=\sqrt{(x / c)^{2}+1}-1 f(x,1,c)=(x/c)2+1−1
该损失也常常被称为Charbonnier loss、pseudoHuber loss (或Huber loss )或L1-L2损失(在零点附近像L2损失,但是在其他地方像L1损失)。
实际上,广义的Charbonnier loss就有同时表达L2以及smooth L1损失的能力,在深度估计任务以及光流任务中有被使用到,其通常被定义为:
( x 2 + ϵ 2 ) α / 2 \left(x^{2}+\epsilon^{2}\right)^{\alpha / 2} (x2+ϵ2)α/2
对式(1)来说,当 α = 0 \alpha=0 α=0时没有定义,然而,当 α \alpha α趋近于0时,极限趋近于Cauchy,又名Lorentzian损失:
lim α → 0 f ( x , α , c ) = log ( 1 2 ( x / c ) 2 + 1 ) \lim _{\alpha \rightarrow 0} f(x, \alpha, c)=\log \left(\frac{1}{2}(x / c)^{2}+1\right) α→0limf(x,α,c)=log(21(x/c)2+1)
当 α = − 2 \alpha=-2 α=−2时,广义损失函数的形式变换为:
f ( x , − 2 , c ) = 2 ( x / c ) 2 ( x / c ) 2 + 4 f(x,-2, c)=\frac{2(x / c)^{2}}{(x / c)^{2}+4} f(x,−2,c)=(x/c)2+42(x/c)2
即Geman-McClure损失。
当 α \alpha α趋近于负无穷时,损失则变为Welsch,或者说Leclerc损失:
lim α → − ∞ f ( x , α , c ) = 1 − exp ( − 1 2 ( x / c ) 2 ) \lim _{\alpha \rightarrow-\infty} f(x, \alpha, c)=1-\exp \left(-\frac{1}{2}(x / c)^{2}\right) α→−∞limf(x,α,c)=1−exp(−21(x/c)2)
根据以上的分析,可以得到广义损失函数的最终形式:
ρ ( x , α , c ) = { 1 2 ( x / c ) 2 if α = 2 log ( 1 2 ( x / c ) 2 + 1 ) if α = 0 1 − exp ( − 1 2 ( x / c ) 2 ) if α = − ∞ ∣ α − 2 ∣ α ( ( ( x / c ) 2 ∣ α − 2 ∣ + 1 ) α / 2 − 1 ) otherwise \rho(x, \alpha, c)= \begin{cases}\frac{1}{2}(x / c)^{2} & \text { if } \alpha=2 \\ \log \left(\frac{1}{2}(x / c)^{2}+1\right) & \text { if } \alpha=0 \\ 1-\exp \left(-\frac{1}{2}(x / c)^{2}\right) & \text { if } \alpha=-\infty \\ \frac{|\alpha-2|}{\alpha}\left(\left(\frac{(x / c)^{2}}{|\alpha-2|}+1\right)^{\alpha / 2}-1\right) & \text { otherwise }\end{cases} ρ(x,α,c)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧21(x/c)2log(21(x/c)2+1)1−exp(−21(x/c)2)α∣α−2∣((∣α−2∣(x/c)2+1)α/2−1) if α=2 if α=0 if α=−∞ otherwise
其对应的梯度形式为:
∂ ρ ∂ x ( x , α , c ) = { x c 2 if α = 2 2 x x 2 + 2 c 2 if α = 0 x c 2 exp ( − 1 2 ( x / c ) 2 ) if α = − ∞ x c 2 ( ( x / c ) 2 ∣ α − 2 ∣ + 1 ) ( α / 2 − 1 ) otherwise \frac{\partial \rho}{\partial x}(x, \alpha, c)= \begin{cases}\frac{x}{c^{2}} & \text { if } \alpha=2 \\ \frac{2 x}{x^{2}+2 c^{2}} & \text { if } \alpha=0 \\ \frac{x}{c^{2}} \exp \left(-\frac{1}{2}(x / c)^{2}\right) & \text { if } \alpha=-\infty \\ \frac{x}{c^{2}}\left(\frac{(x / c)^{2}}{|\alpha-2|}+1\right)^{(\alpha / 2-1)} & \text { otherwise }\end{cases} ∂x∂ρ(x,α,c)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧c2xx2+2c22xc2xexp(−21(x/c)2)c2x(∣α−2∣(x/c)2+1)(α/2−1) if α=2 if α=0 if α=−∞ otherwise
广义损失函数以及对应的梯度的示意图如下图所示:
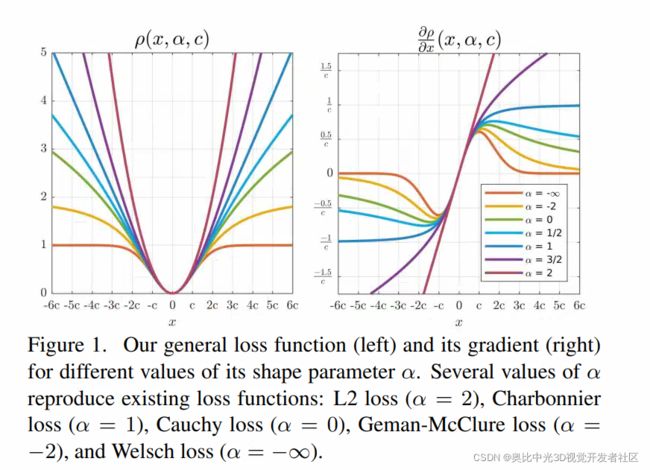
对于所有的 α \alpha α来说,当 ∣ x ∣ < c |x|
当 α = 2 \alpha=2 α=2时,导数的大小与残差的大小一直呈正比,也就是说,更大的残差将相应地有更大的影响;倾向于估计残差均值。
当 α = 1 \alpha = 1 α=1时,当残差大于 c c c时,导数大小将在 1 c \frac{1}{c} c1处达到饱和,即,当残差大于一定数值后,尽管其影响不会下降,但是也不会超过某一个具体的数值;倾向于估计残差中值。
当 α < 1 \alpha <1 α<1时,当残差 ∣ x ∣ > c |x|>c ∣x∣>c时,残差影响将会下降,即,对于outlier的增加,其在梯度下降中将会有着更少的影响;当 α \alpha α的数值越小,outlier的影响就越小,尤其当 α \alpha α趋向负无穷时,大于 3 c 3c 3c的残差几乎没有梯度回传(等价于local mode-finding)。
此外,该广义损失函数的其他性质有:
-
在0点处导数为0,且单调递增;
-
当尺度因子 c c c与残差 x x x同时增大时,损失不变: ∀ k > 0 ρ ( k x , α , k c ) = ρ ( x , α , c ) \forall_{k>0} \rho(k x, \alpha, k c)=\rho(x, \alpha, c) ∀k>0ρ(kx,α,kc)=ρ(x,α,c);
-
损失函数对 α \alpha α的偏导大于0,即 α \alpha α越大,损失越大: ∂ ρ ∂ α ( x , α , c ) ≥ 0 \frac{\partial \rho}{\partial \alpha}(x, \alpha, c) \geq 0 ∂α∂ρ(x,α,c)≥0;该性质的好处是,我们可以先初始化一个 α \alpha α,使得损失函数是一个凸函数,然后再慢慢地减小 α \alpha α,进而在实现鲁棒估计的同时,避免陷入局部最小值。当 α \alpha α趋向于正无穷时,我们可以取得梯度的上界为:
ρ ( x , α , c ) ≤ lim α → + ∞ ρ ( x , α , c ) = exp ( 1 2 ( x / c ) 2 ) − 1 \rho(x, \alpha, c) \leq \lim _{\alpha \rightarrow+\infty} \rho(x, \alpha, c)=\exp \left(\frac{1}{2}(x / c)^{2}\right)-1 ρ(x,α,c)≤α→+∞limρ(x,α,c)=exp(21(x/c)2)−1据此,我们可以限制损失的梯度,避免梯度爆炸的问题,即:
∣ ∂ ρ ∂ x ( x , α , c ) ∣ ≤ { 1 c ( α − 2 α − 1 ) ( α − 1 2 ) ≤ 1 c if α ≤ 1 ∣ x ∣ c 2 if α ≤ 2 \left|\frac{\partial \rho}{\partial x}(x, \alpha, c)\right| \leq \begin{cases}\frac{1}{c}\left(\frac{\alpha-2}{\alpha-1}\right)^{\left(\frac{\alpha-1}{2}\right)} \leq \frac{1}{c} & \text { if } \alpha \leq 1 \\ \frac{|x|}{c^{2}} & \text { if } \alpha \leq 2\end{cases} ∣∣∣∣∂x∂ρ(x,α,c)∣∣∣∣≤{c1(α−1α−2)(2α−1)≤c1c2∣x∣ if α≤1 if α≤2
实际上,该广义损失函数不能够表达 L 1 L1 L1损失,但是如果 c c c远小于残差 x x x,那么我们可以近似的使用 α = 1 \alpha =1 α=1来近似:
f ( x , 1 , c ) ≈ ∣ x ∣ c − 1 if c ≪ x f(x, 1, c) \approx \frac{|x|}{c}-1 \quad \text { if } c \ll x f(x,1,c)≈c∣x∣−1 if c≪x
概率密度函数
通过广义损失函数,可以构建一个通用的概率分布,使得其概率分布函数(简称PDF)的负对数似然(Negative log-likelihood,简称NLL)是广义损失函数的平移版本:
p ( x ∣ μ , α , c ) = 1 c Z ( α ) exp ( − ρ ( x − μ , α , c ) ) p(x \mid \mu, \alpha, c)=\frac{1}{c Z(\alpha)} \exp (-\rho(x-\mu, \alpha, c)) p(x∣μ,α,c)=cZ(α)1exp(−ρ(x−μ,α,c))
Z ( α ) = ∫ − ∞ ∞ exp ( − ρ ( x , α , 1 ) ) Z(\alpha)=\int_{-\infty}^{\infty} \exp (-\rho(x, \alpha, 1)) Z(α)=∫−∞∞exp(−ρ(x,α,1))
其中, p ( x ∣ μ , α , c ) p(x \mid \mu, \alpha, c) p(x∣μ,α,c)仅在 α > 0 \alpha > 0 α>0时才有定义,因为当 α < 0 \alpha <0 α<0时, Z ( α ) Z(\alpha) Z(α)是发散的。
对于某些特定的值,有:
Z ( 0 ) = π 2 Z ( 1 ) = 2 e K 1 ( 1 ) Z ( 2 ) = 2 π Z ( 4 ) = e 1 / 4 K 1 / 4 ( 1 / 4 ) \begin{array}{ll} Z(0)=\pi \sqrt{2} & Z(1)=2 e K_{1}(1) \\ Z(2)=\sqrt{2 \pi} & Z(4)=e^{1 / 4} K_{1 / 4}(1 / 4) \end{array} Z(0)=π2Z(2)=2πZ(1)=2eK1(1)Z(4)=e1/4K1/4(1/4)
其中, K n ( ⋅ ) K_n(\cdot) Kn(⋅)是第二类修正贝塞尔函数。对于任何的正有理数 α \alpha α(除去没有定义的 α \alpha α=2),且 α = n / d \alpha = n/d α=n/d,其中 n n n和 d d d都是整数,则有:
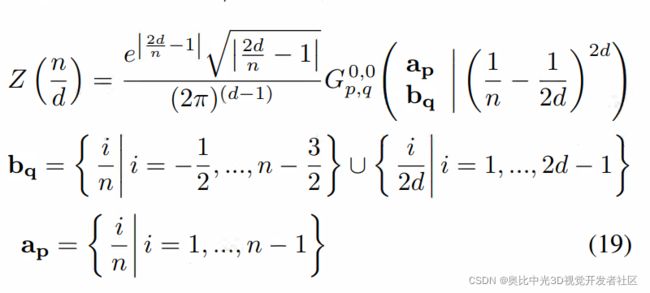
实际在实验中, l o g ( Z ( α ) ) log(Z(\alpha)) log(Z(α))是通过使用三次hermite样条函数得到的。
当 α = 2 \alpha = 2 α=2时,残差的分布为高斯分布;
当 α = 0 \alpha = 0 α=0时,残差的分布为Cauchy分布。
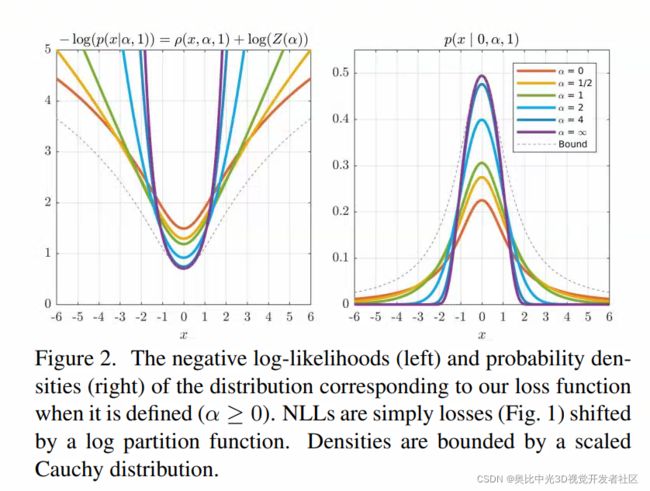
广义损失函数的分布模拟了广义高斯分布,唯一的不同在于广义损失函数的分布是“平滑的”,即,不管 α \alpha α的数值是多少,在零点附近都是高斯分布。对于不同的 α \alpha α所对应的PDF和NLL如下图所示
在后续的实验中,将使用广义分布的负对数形式 − log ( p ( ⋅ ∣ α , c ) ) -\log (p(\cdot \mid \alpha, c)) −log(p(⋅∣α,c))作为损失函数,而非广义损失函数 ρ ( ⋅ , α , c ) \rho(\cdot, \alpha, c) ρ(⋅,α,c)。这样做的原因是,使用NLL的形式允许将 α \alpha α视作一个参数,进而使得网络自己去学习到合适的 α \alpha α。为了能够进一步地理解这样做的原因,我们思考两个场景:
- 先思考这样一个场景,在训练过程中,我们需要优化的只有网络模型的权重以及参数 α \alpha α,即 ρ ( ⋅ , α , c ) \rho(\cdot, \alpha, c) ρ(⋅,α,c)。在这个场景中,由于我们已经知道损失会随着 α \alpha α的增大而增大,所以如果我们想要减少粗差的影响,我们只需要将 α \alpha α尽可能地设小就可以。
- 再思考另一个场景,仍然在训练过程中,如果我们要优化分布的NLL,而不是损失,那么从figure2中可见,减小 α \alpha α虽然可以减少NLL的outliers,但是也进而会增加其inliers的代价。在训练的过程中,网络需要去选择,是减小 α \alpha α来减少粗差上的影响却要增加inliers的影响,还是要增大 α \alpha α来增大粗差上的影响却要减少inliers的影响,这迫使网络自己去做trade-off,进而得到一个比较合适的 α \alpha α值。后续的实验也表明这么做确实能够适应许多应用场景,且避免了手动调参的麻烦。
由于NLL已经有所限定,从分布中抽样变得非常直观。由于分布是一系列位置与尺度的侯选池,因此我们直接从 p ( x ∣ 0 , α , 1 ) p(x \mid 0, \alpha, 1) p(x∣0,α,1)进行采样,然后再通过参数 c c c和 μ \mu μ对其进行尺度变换以及平移。
这样的采样方法是非常高效的,采样接收率在大约45%( α = ∞ \alpha = \infin α=∞)至100%( α = 0 \alpha =0 α=0)之间。
实验
共进行了四个实验,没有一个实验要去逼近sota,因为实验目的只是想要证明损失函数以及分布的价值,即,只是更换任务中的损失函数,就可以获得大幅的结果提升。
在前两个实验中,重点关注基于深度学习的视觉任务,训练目标关注于最小化影像之间的差别:用于影像合成的变分自编码器以及自监督的单目深度估计。
具体地,将使用广义分布(作为生成模型中的条件分布或者使用其NLL形式作为自适应损失)且允许分布自动地选取“鲁棒性”参数。由于“鲁棒性”参数是自动选取的,且并不需要人工调参,因此我们不妨大胆设想,为什么不为输出的每一个维度都给定专属的鲁棒性参数呢?比如说我们可以为输出图像的每一个像素都学一个“鲁棒性”参数。之后的实验结果可以证明这样的想法和不同图像表达(比如小波)相结合的时候尤其有效。
在第三、四个实验中,我们将在两个传统任务中证明该损失函数的价值。具体地,将替换传统算法中固定的损失为广义损失函数,且引入一个可调的“鲁棒性”参数 α \alpha α。参数 α \alpha α既可以为人工调,也可以进行退火。
变分自编码器
所谓的变分自编码器指将自编码器训练成生成式模型任务中的一个里程碑式工作,其可使得随意画的样例转变为可用的训练数据。
而在本实验中,目的则为证明广义分布可以被用于提高在VAEs中的对数似然表现,具体地,可以在CelebA数据集上进行影像合成的试验。一种通用的VAEs的设计是,对影像的RGB向量使用独立正态分布进行建模,在本实验中,则采用这种设计作为baseline。
在当时做的相对比较好的工作中,采用了"adversarial"损失函数(Dosovitskiy 等,2016;Goodfellow等,2014;Cohen等,1992)。在本实验中,主要是想去探索一个假设是否正确,即,在每一个像素的影像表达上进行正态分布的建模时,是否可以通过使用广义分布对VAEs输出做变换,而得到效果上的大幅提升。
在作为对照组的baseline模型中,我们为每一个像素的正态分布给定一个尺度参数 σ i \sigma^{i} σi,该尺度参数将在训练中被优化,进而使得VAE在输出的所有维度上自适应地进行尺度适应。而在实验组中,我们可以直观地将输出中每个像素的正态分布改为广义分布,这样的话,输出的每一个维度都有两个参数,一个是 α ( i ) \alpha^{(i)} α(i),再一个就是 c ( i ) c^{(i)} c(i)(相当于 σ ( i ) \sigma^{(i)} σ(i))。我们不妨让 α ( i ) \alpha^{(i)} α(i)与 c ( i ) c^{(i)} c(i)一同变为自由参数,进而使得VAE进行自适应的选择。更为具体地,我们将所有的 α ( i ) \alpha^{(i)} α(i)限制在 ( 0 , 3 ) (0,3) (0,3)之间,这使得分布可以具象化为Cauchy( α = 0 \alpha = 0 α=0)分布以及正态分布 ( α = 2 ) (\alpha = 2) (α=2),二者之间的分布,以及其他更为宽峰的分布 ( α > 2 ) (\alpha >2) (α>2)。将 α \alpha α限制在3以内,主要是考虑了在训练过程中 α \alpha α的增加会带来训练的不稳定性。
考虑到具体的实现,对于每一个输出维度 i i i,我们构建了变量 { α l ( i ) } \{\alpha_{l}^{(i)}\} {αl(i)}以及 { c l ( i ) } \{c_{l}^{(i)}\} {cl(i)},并且有以下定义:
α ( i ) = ( α max − α min ) sigmoid ( α ℓ ( i ) ) + α min c ( i ) = softplus ( c ℓ ( i ) ) + c min α min = 0 , α max = 3 , c min = 1 0 − 8 \begin{gathered} \alpha^{(i)}=\left(\alpha_{\max }-\alpha_{\min }\right) \operatorname{sigmoid}\left(\alpha_{\ell}^{(i)}\right)+\alpha_{\min } \\ c^{(i)}=\operatorname{softplus}\left(c_{\ell}^{(i)}\right)+c_{\min } \\ \alpha_{\min }=0, \alpha_{\max }=3, c_{\min }=10^{-8} \end{gathered} α(i)=(αmax−αmin)sigmoid(αℓ(i))+αminc(i)=softplus(cℓ(i))+cminαmin=0,αmax=3,cmin=10−8
其中, c m i n c_{min} cmin作为偏移量,可以避免 c ( i ) c^{(i)} c(i)在训练中退化为0, α m i n \alpha_{min} αmin以及 α m a x \alpha_{max} αmax定义了 α ( i ) \alpha^{(i)} α(i)的取值范围。在初始情况下,所有的 α ( i ) \alpha^{(i)} α(i)被设置为1,而所有的 c ( i ) c^{(i)} c(i)被设置为0.01,且在后续的训练中,与自编码器的权重一同通过Adam优化器进行优化。
尽管使用独立分布对图像输出的每一个像素进行建模是很流行的选择,但是在Field等(1987),Mallat等(1987)类似于小波分解的工作中表明重尾分布(heavy-tailed distributions)可能会有着更好的建模效果。基于此,我们额外训练了一个模型,在该模型中,我们在计算广义分布的NLL之前对RGB影像进行解码。为此,使用了DCT(Ahmed等,1974)以及CDF 9/7小波分解,以及YUV的色彩空间。
这些表达分别仿照了JPEG以及JPEG 2000的压缩标准。
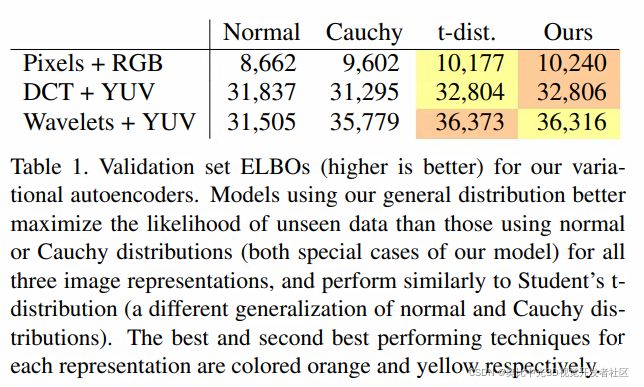
表中报告了不同分布和影像表达组合,在ELBO(evidence lower bound)指标上的结果。
由图表可见,广义分布的效果与学生t分布的结果比较相似,二者都有着高ELBOs。此外,二者似乎有着互补的优势,广义分布体现更为宽峰,而学生t分布则表现的更为窄峰。然而,相比起广义分布,学生t分布不能够具象化到Charbonnier等分布的形式上。对于所有的表达形式来说,使用广义分布训练得到的VAEs会产生更为锐利和细节更好的结果。而使用Cauchy以及t分布训练得到的模型则将保持高频信息,且在像素表达上工作的不错,然而在合成低频信息的时候,比如说背景,则会有大幅的失效。对于所有的影像表达,最好的表达形式为小波+YUV的组合,我们发现尽管是正态分布,小波+YUV的组合也能得到非常好的结果,这说明将分布与影像表达进行结合是非常有用的。
在训练之后, { α ( i ) } \{\alpha^{(i)}\} {α(i)}在 ( 0 , 2.5 ) (0,2.5) (0,2.5)范围内波动,也就是说,正态分布和类似于Cauchy分布的自适应混合是有用的,这也与Portilla等人(2003)的发现一致。
综上,所谓的自适应的鲁棒性不过是让 { α l ( i ) } \{\alpha_l^{(i)}\} {αl(i)}变为训练中的自由变量。
无监督的单目深度估计
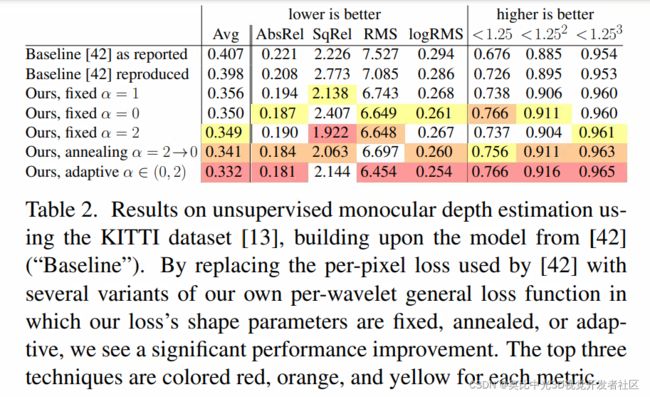
使用Zhou等人(2017)所提出的模型作为基础模型,这个模型训练的目的是减少warp后的右图与左图之间的差别,具体地,所谓的差别由RGB值的绝对偏差表示。仍然,实验将训练指标替换为广义损失函数,并希望证明使用退火或是自适应的形式可以提高模型精度。
损失的绝对值,相当于固定尺度的拉普拉斯分布的最大似然。那么,我们将固定的拉普拉斯分布替换成广义分布,使得尺度固定,但是允许参数 α \alpha α进行变化。此外,不同于原模型在RGB分量上进行损失计算,实验在YUV+小波的组合表示上进行损失计算。
训练以及验证均在KITTI数据集上进行。
快速全局配准任务
在传统几何配准中,鲁棒性几乎是必须考虑的因素。快速全局配准算法通过最小化以下损失,进而找到两个点集 { p } \{p\} {p}和 { q } \{q\} {q}之间的刚性变化 T T T:
∑ ( p , q ) ρ g m ( ∥ p − T q ∥ , c ) \sum_{(\mathbf{p}, \mathbf{q})} \rho_{g m}(\|\mathbf{p}-\mathbf{T} \mathbf{q}\|, c) (p,q)∑ρgm(∥p−Tq∥,c)
其中 ρ g m ( ⋅ ) \rho_{gm}(\cdot) ρgm(⋅)是Geman-McClure损失。显然,Geman-McClure是广义损失中的一个特例( α = − 2 \alpha=-2 α=−2)。我们将使用广义损失函数的快速全局配准算法简称为gFGR(generalized FGR, 简称gFGR)。FGR在退火尺度参数 c c c时,同时求解线性系统,而 g F G R gFGR gFGR则提供了一种替代的策略,即,退火鲁棒性参数 α \alpha α而非尺度参数 c c c,形成一种“形状退火”的形式。具体地,这种“形状退火”的过程为:
在64次迭代中,每隔四次迭代退火一次,退火值为:
2,1,1/2,1/4,0,-1/4,-1/2,-1,-2,-4,-8,-16,-32
与Zhou等人(2016)的结果相比,gFGR在高噪声输入时获得了可观的提升,而在低噪声输入时则保持了高质量,具体结果见下表:
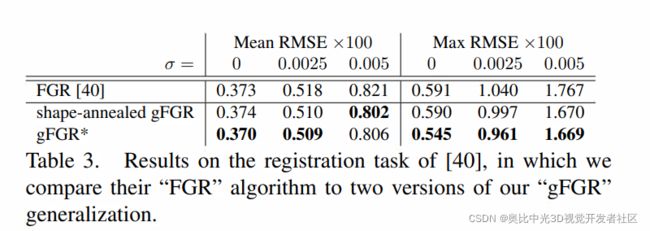
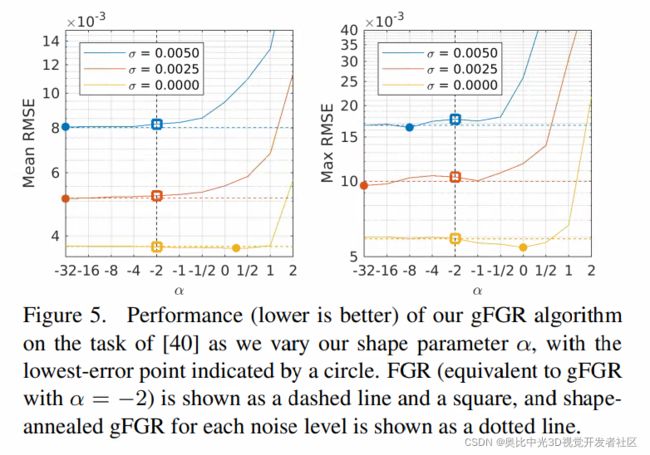
此外,还有另一种策略是,仍然对 c c c进行退火,但是将 α \alpha α视作一个超参数,并且独立地根据噪声情况对其进行调整。在Figure 5中,将 α \alpha α设置为一系列不同的值,观察误差情况,可以发现,对于高噪声的输入来说, α \alpha α设置为负数的时候会更好,而当输入为低噪声时, α \alpha α设置为0时会更好,Figure5见下图:
在Table 3中,报告了对于每一个噪声层级最低的误差,命名为 g F G R ∗ gFGR^* gFGR∗。
鲁棒连续聚类任务
在Shan等人(2017)的工作中,将鲁棒性损失用于无监督的聚类工作,用于最小化下式:
∑ i ∥ x i − u i ∥ 2 2 + λ ∑ ( p , q ) ∈ E w p , q ρ g m ( ∥ u p − u q ∥ 2 ) \sum_{i}\left\|\mathbf{x}_{i}-\mathbf{u}_{i}\right\|_{2}^{2}+\lambda \sum_{(p, q) \in \mathcal{E}} w_{p, q} \rho_{g m}\left(\left\|\mathbf{u}_{p}-\mathbf{u}_{q}\right\|_{2}\right) i∑∥xi−ui∥22+λ(p,q)∈E∑wp,qρgm(∥up−uq∥2)
其中, { x i } \{x_i\} {xi}是一系列输入的数据点, { u i } \{u_i\} {ui}是一系列聚类的中心, E \mathcal{E} E则是一个m-KNN(mutual k-nearest)图, ρ g m \rho_{gm} ρgm仍为Geman-McClure损失。
仍然,我们将 ρ g m \rho_{gm} ρgm替换为广义损失函数,不同 α \alpha α取值导致的结果如下图所示:
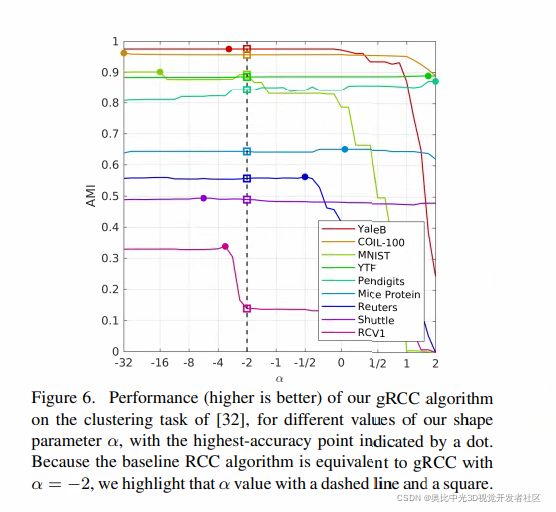
可以发现,对于不同数据集,广义损失函数的优势程度不同,有些数据集对于 α \alpha α并不敏感,而敏感的,指标提升有32%之多。
推测结论:广义损失函数与数据有较强相关性。
结论
广义损失函数是一个可以兼容多种特定损失函数(如 welsch、smooth L1等)的形式,具有优美的数学形式,且其可以将“鲁棒性”视作一个连续变量,进而根据需求形成鲁棒的损失函数引导。此外,作者本质上给读者提供了两种参数设置的方式,一种是自适应的参数设置,无需人工调整,但是其限制在于未包含鲁棒性参数在负值时的情况,另一种则是人工设置的方式,既可应用至深度学习方法中,亦可应用于传统方法中。
参考文献
- Qian-Yi Zhou, Jaesik Park, and Vladlen Koltun. Fast global registration. ECCV, 2016.
- Sohil Atul Shah and Vladlen Koltun. Robust continuous clustering. PNAS, 2017.
- Tinghui Zhou, Matthew Brown, Noah Snavely, and David G. Lowe. Unsupervised learning of depth and ego-motion from video. CVPR, 2017.
- Alexey Dosovitskiy and Thomas Brox. Generating images with perceptual similarity metrics based on deep networks. NIPS, 2016.
- Javier Portilla, Vasily Strela, Martin J. Wainwright, and Eero P. Simoncelli. Image denoising using scale mixtures of gaussians in the wavelet domain. IEEE TIP, 2003.
- David J. Field. Relations between the statistics of natural images and the response properties of cortical cells. JOSA A, 1987.
- Stephane Mallat. A theory for multiresolution signal decomposition: The wavelet representation. TPAMI, 1989.
- Nasir Ahmed, T Natarajan, and Kamisetty R Rao. Discrete cosine transform. IEEE Transactions on Computers, 1974.
- Albert Cohen, Ingrid Daubechies, and J-C Feauveau. Biorthogonal bases of compactly supported wavelets. Communications on pure and applied mathematics, 1992
版权声明:本文为奥比中光3D视觉开发者社区特约作者授权原创发布,未经授权不得转载,本文仅做学术分享,版权归原作者所有,若涉及侵权内容请联系删文
3D视觉开发者社区是由奥比中光给所有开发者打造的分享与交流平台,旨在将3D视觉技术开放给开发者。平台为开发者提供3D视觉领域免费课程、奥比中光独家资源与专业技术支持。点击加入3D视觉开发者社区,和开发者们一起讨论分享吧~
也可移步微信关注官方公众号 3D视觉开发者社区 ,获取更多干货知识哦