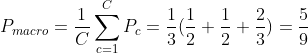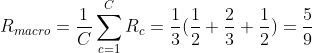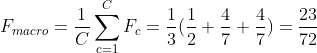HBU-NNDL 实验三 线性回归
2.2 线性回归
回归:一个或多个自变量与因变量之间的关系之间建模的方法,经常用来表示输入和输出之间的关系
分类:预测数据属于一组类别的哪一个
一个简单的线性模型
- 线性回归是对n维输入的加权,外加偏差
- 使用平方损失来衡量预测值与真实值的差异(乘1/2为了求导方便,并没有太大影行)
- 线性回归有显示解
- 线性回归可以看成单层神经网络
2.2.1 数据集构建
首先,我们构造一个小的回归数据集。假设输入特征和输出标签的维度都为 1,需要被拟合的函数定义为:
def linear_func(x, w=1.2, b=0.5):
y = w * x + b
return y此函数返回的是y = 1.2*x+0.5这个函数
def create_toy_data(func, interval, sample_num, noise = 0.0, add_outlier = False, outlier_ratio = 0.001):
"""
根据给定的函数,生成样本
输入:
- func:函数
- interval: x的取值范围
- sample_num: 样本数目
- noise: 噪声均方差
- add_outlier:是否生成异常值
- outlier_ratio:异常值占比
输出:
- X: 特征数据,shape=[n_samples,1]
- y: 标签数据,shape=[n_samples,1]
"""
# 均匀采样
# 使用paddle.rand在生成sample_num个随机数
X = paddle.rand(shape = [sample_num]) * (interval[1]-interval[0]) + interval[0]
y = func(X)
# 生成高斯分布的标签噪声
# 使用paddle.normal生成0均值,noise标准差的数据
epsilon = paddle.normal(0,noise,paddle.to_tensor(y.shape[0]))
y = y + epsilon
if add_outlier: # 生成额外的异常点
outlier_num = int(len(y)*outlier_ratio) #异常点个数
if outlier_num != 0:
# 使用paddle.randint生成服从均匀分布的、范围在[0, len(y))的随机Tensor
outlier_idx = paddle.randint(len(y),shape = [outlier_num]) #随机生成异常点下标
y[outlier_idx] = y[outlier_idx] * 5 #异常点数值为五倍数值
return X, ytorch.rand()是均匀分布,torch.rand(*size, out=None, dtype=None),因为rand()默认[0,1]范围不能指定范围,所以[m,n]范围内使用torch.rand()*(m-n)+n的范围
关于torch.normal()的用法:
一开始我仿照paddle的参数,epsilon = torch.normal(0.0,noise,torch.tensor(y.shape[0]))
出现如下报错:
TypeError: normal() received an invalid combination of arguments - got (float, int, Tensor), but expected one of:
* (Tensor mean, Tensor std, *, torch.Generator generator, Tensor out)
* (Tensor mean, float std, *, torch.Generator generator, Tensor out)
* (float mean, Tensor std, *, torch.Generator generator, Tensor out)
* (float mean, float std, tuple of ints size, *, torch.Generator generator, Tensor out, torch.dtype dty
之后发现torch的用法不同,torch.normal(mean, std, size, *, out=None) → Tensor
所有绘制的元素都共享平均值和标准差。由此产生的张量大小由大小给定。
size参数要使用元组类型,而不是paddle的tensor类型
from matplotlib import pyplot as plt # matplotlib 是 Python 的绘图库
func = linear_func
interval = (-10,10)
train_num = 100 # 训练样本数目
test_num = 50 # 测试样本数目
noise = 2
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise, add_outlier = False)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise, add_outlier = False)
X_train_large, y_train_large = create_toy_data(func=func, interval=interval, sample_num=5000, noise = noise, add_outlier = False)
# torch.linspace返回一个Tensor,Tensor的值为在区间start和stop上均匀间隔的num个值,输出Tensor的长度为num
X_underlying = torch.linspace(interval[0],interval[1],train_num)
y_underlying = linear_func(X_underlying)
# 绘制数据
plt.scatter(X_train, y_train, marker='*', facecolor="none", edgecolor='#e4007f', s=50, label="train data")
plt.scatter(X_test, y_test, facecolor="none", edgecolor='#f19ec2', s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"underlying distribution")
plt.legend(fontsize='x-large') # 给图像加图例
plt.savefig('ml-vis.pdf') # 保存图像到PDF文件中
plt.show()2.2.2 模型构建
在线性回归中,自变量为样本的特征向量x∈RDx∈RD(每一维对应一个自变量),因变量是连续值的标签y∈Ry∈R。
线性模型定义为:![]()
样本的矩阵![]() 是由N个x的行向量组成。而原教材中x为列向量,其特征矩阵与本书中的特征矩阵刚好为转置关系。
是由N个x的行向量组成。而原教材中x为列向量,其特征矩阵与本书中的特征矩阵刚好为转置关系。
如下是自定义线性算子Op.py
import torch
torch.manual_seed(10) #设置随机种子
class Op(object):
def __init__(self):
pass
def __call__(self, inputs):
return self.forward(inputs)
def forward(self, inputs):
raise NotImplementedError
def backward(self, inputs):
raise NotImplementedError
# 线性算子
class Linear(Op):
def __init__(self, input_size):
"""
输入:
- input_size:模型要处理的数据特征向量长度
"""
self.input_size = input_size
# 模型参数
self.params = {}
self.params['w'] = torch.randn(size=[self.input_size, 1], dtype=torch.float32)
self.params['b'] = torch.zeros(size=[1], dtype=torch.float32)
def __call__(self, X):
return self.forward(X)
# 前向函数
def forward(self, X):
"""
输入:
- X: tensor, shape=[N,D]
注意这里的X矩阵是由N个x向量的转置拼接成的,与原教材行向量表示方式不一致
输出:
- y_pred: tensor, shape=[N]
"""
N, D = X.shape
if self.input_size == 0:
return torch.full(size=[N, 1], fill_value=self.params['b'])
assert D == self.input_size # 输入数据维度合法性验证
# 使用torch.matmul计算两个tensor的乘积
y_pred = torch.matmul(X, self.params['w']) + self.params['b']
return y_predimport torch
from op import Op
torch.manual_seed(10) # 设置随机种子
# 线性算子
class Linear(Op):
def __init__(self, input_size):
"""
输入:
- input_size:模型要处理的数据特征向量长度
"""
self.input_size = input_size
# 模型参数
self.params = {}
self.params['w'] = torch.randn(size=[self.input_size, 1], dtype=torch.float32)
self.params['b'] = torch.zeros(size=[1], dtype=torch.float32)
def __call__(self, X):
return self.forward(X)
# 前向函数
def forward(self, X):
"""
输入:
- X: tensor, shape=[N,D]
注意这里的X矩阵是由N个x向量的转置拼接成的,与原教材行向量表示方式不一致
输出:
- y_pred: tensor, shape=[N]
"""
N, D = X.shape
if self.input_size == 0:
return torch.full(size=[N, 1], fill_value=self.params['b'])
assert D == self.input_size # 输入数据维度合法性验证
# 使用torch.matmul计算两个tensor的乘积
y_pred = torch.matmul(X, self.params['w']) + self.params['b']
return y_pred
# 注意这里我们为了和后面章节统一,这里的X矩阵是由N个x向量的转置拼接成的,与原教材行向量表示方式不一致
input_size = 3
N = 2
X = torch.randn(size=[N, input_size], dtype=torch.float32) # 生成2个维度为3的数据
model = Linear(input_size)
y_pred = model(X)
print("y_pred:", y_pred) # 输出结果的个数也是2个
y_pred: tensor([[1.8529],
[0.6011]])
2.2.3 损失函数
回归任务中常用的评估指标是均方误差
均方误差(mean-square error, MSE)是反映估计量与被估计量之间差异程度的一种度量。
def mean_squared_error(y_true, y_pred):
"""
输入:
- y_true: tensor,样本真实标签
- y_pred: tensor, 样本预测标签
输出:
- error: float,误差值
"""
assert y_true.shape[0] == y_pred.shape[0] #保证真实标签和预测值维度相同
# torch.square计算输入的平方值
# torch.mean沿 axis 计算 x 的平均值,默认axis是None,则对输入的全部元素计算平均值。
error = torch.mean(torch.square(y_true - y_pred))
return error
# 构造一个简单的样例进行测试:[N,1], N=2
y_true = torch.tensor([[-0.2], [4.9]], dtype=torch.float32)
y_pred = torch.tensor([[1.3], [2.5]], dtype=torch.float32)
error = mean_squared_error(y_true=y_true, y_pred=y_pred).item()
print("error:", error)error: 4.005000114440918
关于均方误差的公式:
代码中没有除2,和周老师给出的一样,我认为2的作用是在反向传播更新参数求偏导时,
平方会变成×2,与1/2消掉,更便于计算。无论是1/n,1/2还是1/2n,都对最后结果没有太大影响。
2.2.4 模型优化
参数学习的过程通过优化器完成。由于我们可以基于最小二乘方法可以直接得到线性回归的解析解,此处的训练是求解析解的过程,代码实现如下:
def optimizer_lsm(model, X, y, reg_lambda=0):
"""
输入:
- model: 模型
- X: tensor, 特征数据,shape=[N,D]
- y: tensor,标签数据,shape=[N]
- reg_lambda: float, 正则化系数,默认为0
输出:
- model: 优化好的模型
"""
N, D = X.shape
# 对输入特征数据所有特征向量求平均
x_bar_tran = torch.mean(X, dim=0).T
# 求标签的均值,shape=[1]
y_bar = torch.mean(y)
# torch.subtract通过广播的方式实现矩阵减向量
x_sub = torch.subtract(X, x_bar_tran)
# 使用torch.all判断输入tensor是否全0
if torch.all(x_sub == 0):
model.params['b'] = y_bar
model.params['w'] = torch.zeros(size=[D])
return model
# torch.inverse求方阵的逆
tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
reg_lambda * torch.eye(n=(D)))
w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))
b = y_bar - torch.matmul(x_bar_tran, w)
model.params['b'] = b
model.params['w'] = torch.squeeze(w, dim=-1)
return model思考:
1、 经验风险最小化为了简单起见省略均方误差的系数![]() ,为什么不影响效果?
,为什么不影响效果?
![]() 只是均方误差前的一个系数,不影响得到的最优解
只是均方误差前的一个系数,不影响得到的最优解
2、什么是最小二乘法?
最小二乘法通过最小化误差(真实目标对象与拟合目标对象的差)的平方和寻找数据的最佳函数匹配。最小二乘法同梯度下降类似,都是一种求解无约束最优化问题的常用方法,并且也可以用于曲线拟合,来解决回归问题。
2.2.5 模型训练
在准备了数据、模型、损失函数和参数学习的实现之后,我们开始模型的训练。在回归任务中,模型的评价指标和损失函数一致,都为均方误差。
通过上文实现的线性回归类来拟合训练数据,并输出模型在训练集上的损失。
input_size = 1
model = Linear(input_size)
model = optimizer_lsm(model,X_train.reshape([-1,1]),y_train.reshape([-1,1]))
print("w_pred:",model.params['w'].item(), "b_pred: ", model.params['b'].item())
y_train_pred = model(X_train.reshape([-1,1])).squeeze()
train_error = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
print("train error: ",train_error)
model_large = Linear(input_size)
model_large = optimizer_lsm(model_large,X_train_large.reshape([-1,1]),y_train_large.reshape([-1,1]))
print("w_pred large:",model_large.params['w'].item(), "b_pred large: ", model_large.params['b'].item())
y_train_pred_large = model_large(X_train_large.reshape([-1,1])).squeeze()
train_error_large = mean_squared_error(y_true=y_train_large, y_pred=y_train_pred_large).item()
print("train error large: ",train_error_large)w_pred: 1.2271720170974731 b_pred: 0.37986236810684204
train error: 105.02835083007812
w_pred large: 1.1993684768676758 b_pred large: 0.5421561002731323
train error large: 99.23371124267578
可以看出w与b的的预测值与真实值(1.2,0.5)相近
2.2.6 模型评估
下面用训练好的模型预测一下测试集的标签,并计算在测试集上的损失。
y_test_pred = model(X_test.reshape([-1,1])).squeeze()
test_error = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
print("test error: ",test_error)
y_test_pred_large = model_large(X_test.reshape([-1,1])).squeeze()
test_error_large = mean_squared_error(y_true=y_test, y_pred=y_test_pred_large).item()
print("test error large: ",test_error_large)test error: 90.84951782226562
test error large: 89.00284576416016
2.2.7 样本数量 & 正则化系数
2.2.7.1 调整训练数据的样本数量,由 100 调整到 5000,观察对模型性能的影响。
train_num = 5000 # 训练样本数目 w_pred: 1.197505235671997 b_pred: 0.4983460307121277
train error: 99.06513977050781
w_pred large: 1.2121068239212036 b_pred large: 0.5092155933380127
train error large: 99.74403381347656
test error: 83.19195556640625
test error large: 84.21379089355469
可以看出训练样本越多,w,b越接近真实值,MSE也越低
2.2.7.2 调整正则化系数
def optimizer_lsm(model, X, y, reg_lambda=5):w_pred: 1.1974689960479736 b_pred: 0.49835026264190674
train error: 99.06227111816406
w_pred large: 1.2120693922042847 b_pred large: 0.509216845035553
train error large: 99.74108123779297
test error: 83.189453125
test error large: 84.211181640625
将正则化系数从0调整到5,好像对结果没有太大影响,说明训练模型没有过拟合。
2.3 多项式回归
当自变量和因变量之间并不是线性关系时,我们可以定义非线性基函数对特征进行变换,从而可以使得线性回归算法实现非线性的曲线拟合。
接下来我们基于特征维度为1的自变量介绍多项式回归实验。
2.3.1 数据集构建
假设我们要拟合的非线性函数为一个缩放后的sin函数。
这里仍然使用前面定义的create_toy_data函数来构建训练和测试数据,其中训练数样本 15 个,测试样本 10 个,高斯噪声标准差为 0.1,自变量范围为 (0,1)。
import math
import torch
from matplotlib import pyplot as plt
# sin函数: sin(2 * pi * x)
def sin(x):
y = torch.sin(2 * math.pi * x)
return y
def create_toy_data(func, interval, sample_num, noise = 0.0, add_outlier = False, outlier_ratio = 0.001):
"""
根据给定的函数,生成样本
输入:
- func:函数
- interval: x的取值范围
- sample_num: 样本数目
- noise: 噪声均方差
- add_outlier:是否生成异常值
- outlier_ratio:异常值占比
输出:
- X: 特征数据,shape=[n_samples,1]
- y: 标签数据,shape=[n_samples,1]
"""
# 均匀采样
# 使用torch.rand在生成sample_num个随机数
X = torch.rand(sample_num,1) * (interval[1]-interval[0]) + interval[0]
y = func(X)
# 生成高斯分布的标签噪声
# 使用torch.normal生成0均值,noise标准差的数据
epsilon = torch.normal(0.0,noise,(y.shape[0],1))
y = y + epsilon
if add_outlier: # 生成额外的异常点
outlier_num = int(len(y)*outlier_ratio)
if outlier_num != 0:
# 使用torch.randint生成服从均匀分布的、范围在[0, len(y))的随机Tensor
outlier_idx = torch.randint(0,len(y),size = [outlier_num])
y[outlier_idx] = y[outlier_idx] * 5
return X, y
# 生成数据
func = sin
interval = (0,1)
train_num = 15
test_num = 10
noise = 0.5 #0.1
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise)
X_underlying = torch.linspace(interval[0],interval[1],100)
y_underlying = sin(X_underlying)
# 绘制图像
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
#plt.scatter(X_test, y_test, facecolor="none", edgecolor="r", s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.legend(fontsize='x-large')
plt.savefig('ml-vis2.pdf')
plt.show()
2.3.2 模型构建
通过多项式的定义可以看出,多项式回归和线性回归一样,同样学习参数w,只不过需要对输入特征![]() 根据多项式阶数进行变换。因此,我们可以套用求解线性回归参数的方法来求解多项式回归参数。
根据多项式阶数进行变换。因此,我们可以套用求解线性回归参数的方法来求解多项式回归参数。
首先,我们实现多项式基函数polynomial_basis_function对原始特征x进行转换。
# 多项式转换
def polynomial_basis_function(x, degree=2):
"""
输入:
- x: tensor, 输入的数据,shape=[N,1]
- degree: int, 多项式的阶数
example Input: [[2], [3], [4]], degree=2
example Output: [[2^1, 2^2], [3^1, 3^2], [4^1, 4^2]]
注意:本案例中,在degree>=1时不生成全为1的一列数据;degree为0时生成形状与输入相同,全1的Tensor
输出:
- x_result: tensor
"""
if degree == 0:
return torch.ones(size=x.shape, dtype=torch.float32)
x_tmp = x
x_result = x_tmp
for i in range(2, degree + 1):
x_tmp = torch.multiply(x_tmp, x) # 逐元素相乘
x_result = torch.cat((x_result, x_tmp), dim=-1)
return x_result
# 简单测试
data = [[2], [3], [4]]
X = torch.tensor(data=data, dtype=torch.float32)
degree = 3
transformed_X = polynomial_basis_function(X, degree=degree)
print("转换前:", X)
print("阶数为", degree, "转换后:", transformed_X)转换前: tensor([[2.],
[3.],
[4.]])
阶数为 3 转换后: tensor([[ 2., 4., 8.],
[ 3., 9., 27.],
[ 4., 16., 64.]])
2.3.3 模型训练
对于多项式回归,我们可以同样使用前面线性回归中定义的LinearRegression算子、训练函数train、均方误差函数mean_squared_error。拟合训练数据的目标是最小化损失函数,同线性回归一样,也可以通过矩阵运算直接求出w的值。
我们设定不同的多项式阶,![]() 的取值分别为0、1、3、8,之前构造的训练集上进行训练,观察样本数据对sin曲线的拟合结果。
的取值分别为0、1、3、8,之前构造的训练集上进行训练,观察样本数据对sin曲线的拟合结果。
plt.rcParams['figure.figsize'] = (12.0, 8.0)
for i, degree in enumerate([0, 1, 3, 8]): # []中为多项式的阶数
model = Linear(degree)
X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), degree)
X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), degree)
model = optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1])) # 拟合得到参数
y_underlying_pred = model(X_underlying_transformed).squeeze()
print(model.params)
# 绘制图像
plt.subplot(2, 2, i + 1)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.plot(X_underlying, y_underlying_pred, c='#f19ec2', label="predicted function")
plt.ylim(-2, 1.5)
plt.annotate("M={}".format(degree), xy=(0.95, -1.4))
# plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.legend(loc='lower left', fontsize='x-large')
plt.savefig('ml-vis3.pdf')
plt.show(){'w': tensor([0.]), 'b': tensor(-0.0696)}
{'w': tensor([-2.3304]), 'b': tensor([1.1818])}
{'w': tensor([ 21.8808, -54.1515, 34.8925]), 'b': tensor([-1.7635])}
{'w': tensor([ 74.8716, -183.0369, 15.1581, 454.9547, -566.8822, 357.8563,
-327.5971, 193.6686]), 'b': tensor([-8.8098])}
观察可视化结果,红色的曲线表示不同阶多项式分布拟合数据的结果:
- 当
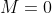 或
或 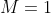 时,拟合曲线较简单,模型欠拟合;
时,拟合曲线较简单,模型欠拟合; - 当
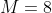 时,拟合曲线较复杂,模型过拟合;
时,拟合曲线较复杂,模型过拟合; - 当
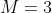 时,模型拟合最为合理。
时,模型拟合最为合理。
2.3.4 模型评估
下面通过均方误差来衡量训练误差、测试误差以及在没有噪音的加入下sin函数值与多项式回归值之间的误差,更加真实地反映拟合结果。多项式分布阶数从0到8进行遍历。
# 训练误差和测试误差
training_errors = []
test_errors = []
distribution_errors = []
# 遍历多项式阶数
for i in range(9):
model = Linear(i)
X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), i)
X_test_transformed = polynomial_basis_function(X_test.reshape([-1, 1]), i)
X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), i)
optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))
y_train_pred = model(X_train_transformed).squeeze()
y_test_pred = model(X_test_transformed).squeeze()
y_underlying_pred = model(X_underlying_transformed).squeeze()
train_mse = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
training_errors.append(train_mse)
test_mse = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
test_errors.append(test_mse)
# distribution_mse = mean_squared_error(y_true=y_underlying, y_pred=y_underlying_pred).item()
# distribution_errors.append(distribution_mse)
print("train errors: \n", training_errors)
print("test errors: \n", test_errors)
# print ("distribution errors: \n", distribution_errors)
# 绘制图片
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.plot(training_errors, '-.', mfc="none", mec='#e4007f', ms=10, c='#e4007f', label="Training")
plt.plot(test_errors, '--', mfc="none", mec='#f19ec2', ms=10, c='#f19ec2', label="Test")
# plt.plot(distribution_errors, '-', mfc="none", mec="#3D3D3F", ms=10, c="#3D3D3F", label="Distribution")
plt.legend(fontsize='x-large')
plt.xlabel("degree")
plt.ylabel("MSE")
plt.savefig('ml-mse-error.pdf')
plt.show()train errors:
[0.6441656947135925, 0.8283544778823853, 0.9778935313224792, 1.087277889251709, 1.0901203155517578, 1.1170716285705566, 1.0674344301223755, 2.0862534046173096, 3.8148746490478516]
test errors:
[0.6824741959571838, 1.1624795198440552, 2.524428606033325, 1.041847586631775, 1.0281134843826294, 1.130333662033081, 1.6590303182601929, 4.540024280548096, 8.942521095275879]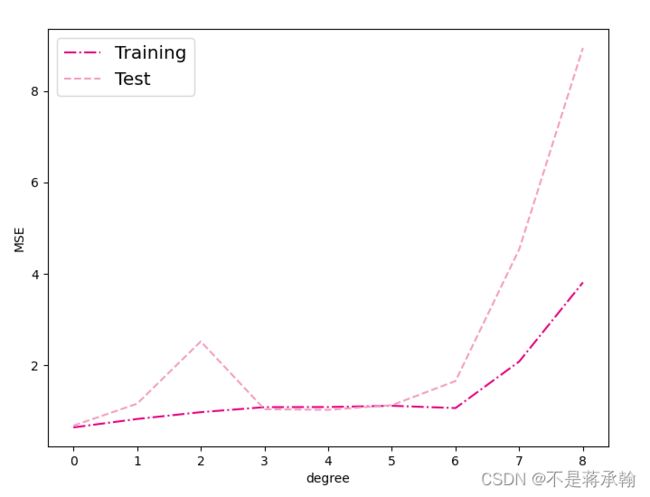
观察可视化结果:
- 当阶数较低的时候,模型的表示能力有限,训练误差和测试误差都很高,代表模型欠拟合;
- 当阶数较高的时候,模型表示能力强,但将训练数据中的噪声也作为特征进行学习,一般情况下训练误差继续降低而测试误差显著升高,代表模型过拟合。
此处多项式阶数大于等于5时,训练误差并没有下降,尤其是在多项式阶数为7时,训练误差变得非常大,请思考原因?提示:请从幂函数特性角度思考。
在前面的求解过程中,没有加惩罚项,此时随着阶数![]() 的增大,
的增大,![]() 往往具有较大的绝对值,从而赋予多项式函数
往往具有较大的绝对值,从而赋予多项式函数![]() 更强的变化能力。
更强的变化能力。
对于模型过拟合的情况,可以引入正则化方法,通过向误差函数中添加一个惩罚项来避免系数倾向于较大的取值。下面加入l2正则化项,查看拟合结果。
degree = 8 # 多项式阶数
reg_lambda = 0.0001 # 正则化系数
X_train_transformed = polynomial_basis_function(X_train.reshape([-1,1]), degree)
X_test_transformed = polynomial_basis_function(X_test.reshape([-1,1]), degree)
X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1,1]), degree)
model = Linear(degree)
optimizer_lsm(model,X_train_transformed,y_train.reshape([-1,1]))
y_test_pred=model(X_test_transformed).squeeze()
y_underlying_pred=model(X_underlying_transformed).squeeze()
model_reg = Linear(degree)
optimizer_lsm(model_reg,X_train_transformed,y_train.reshape([-1,1]),reg_lambda=reg_lambda)
y_test_pred_reg=model_reg(X_test_transformed).squeeze()
y_underlying_pred_reg=model_reg(X_underlying_transformed).squeeze()
mse = mean_squared_error(y_true = y_test, y_pred = y_test_pred).item()
print("mse:",mse)
mes_reg = mean_squared_error(y_true = y_test, y_pred = y_test_pred_reg).item()
print("mse_with_l2_reg:",mes_reg)
# 绘制图像
plt.scatter(X_train, y_train, facecolor="none", edgecolor="#e4007f", s=50, label="train data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.plot(X_underlying, y_underlying_pred, c='#e4007f', linestyle="--", label="$deg. = 8$")
plt.plot(X_underlying, y_underlying_pred_reg, c='#f19ec2', linestyle="-.", label="$deg. = 8, \ell_2 reg$")
plt.ylim(-1.5, 1.5)
plt.annotate("lambda={}".format(reg_lambda), xy=(0.82, -1.4))
plt.legend(fontsize='large')
plt.savefig('ml-vis4.pdf')
plt.show() mse: 8.942521095275879
mse_with_l2_reg: 1.1742827892303467
观察可视化结果,其中点线为加入l2正则后多项式分布拟合结果,虚线为未加入l2正则的拟合结果,点线的拟合效果明显好于红色曲线。
2.4 Runner类介绍
通过上面的实践,我们可以看到,在一个任务上应用机器学习方法的流程基本上包括:数据集构建、模型构建、损失函数定义、优化器、模型训练、模型评价、模型预测等环节。
为了更方便地将上述环节规范化,我们将机器学习模型的基本要素封装成一个Runner类。除上述提到的要素外,再加上模型保存、模型加载等功能。
Runner类的成员函数定义如下:
- __init__函数:实例化Runner类时默认调用,需要传入模型、损失函数、优化器和评价指标等;
- train函数:完成模型训练,指定模型训练需要的训练集和验证集;
- evaluate函数:通过对训练好的模型进行评价,在验证集或测试集上查看模型训练效果;
- predict函数:选取一条数据对训练好的模型进行预测;
- save_model函数:模型在训练过程和训练结束后需要进行保存;
- load_model函数:调用加载之前保存的模型。
import torch
import os
class Runner(object):
def __init__(self, model, optimizer, loss_fn, metric):
# 优化器和损失函数为None,不再关注
# 模型
self.model = model
# 评估指标
self.metric = metric
# 优化器
self.optimizer = optimizer
def train(self, dataset, reg_lambda, model_dir):
X, y = dataset
self.optimizer(self.model, X, y, reg_lambda)
# 保存模型
self.save_model(model_dir)
def evaluate(self, dataset, **kwargs):
X, y = dataset
y_pred = self.model(X)
result = self.metric(y_pred, y)
return result
def predict(self, X, **kwargs):
return self.model(X)
def save_model(self, model_dir):
if not os.path.exists(model_dir):
os.makedirs(model_dir)
params_saved_path = os.path.join(model_dir, 'params.pdtensor')
torch.save(self.model.params, params_saved_path)
def load_model(self, model_dir):
params_saved_path = os.path.join(model_dir, 'params.pdtensor')
self.model.params = torch.load(params_saved_path)
在save()函数中,我将原本的 model.params改为self.model.params,不然训练结果总是不对,这个改动困扰了我好长时间。
下面是引入的优化器函数:
def optimizer_lsm(model, X, y, reg_lambda=0):
"""
输入:
- model: 模型
- X: tensor, 特征数据,shape=[N,D]
- y: tensor,标签数据,shape=[N]
- reg_lambda: float, 正则化系数,默认为0
输出:
- model: 优化好的模型
"""
N, D = X.shape
# 对输入特征数据所有特征向量求平均
x_bar_tran = torch.mean(X,dim=0).T
# 求标签的均值,shape=[1]
y_bar = torch.mean(y)
# torch.subtract通过广播的方式实现矩阵减向量
x_sub = torch.subtract(X,x_bar_tran)
# 使用torch.all判断输入tensor是否全0
if torch.all(x_sub==0):
model.params['b'] = y_bar
model.params['w'] = torch.zeros(size=[D])
return model
# torch.inverse求方阵的逆
tmp = torch.inverse(torch.matmul(x_sub.T,x_sub)+
reg_lambda*torch.eye(n = (D)))
w = torch.matmul(torch.matmul(tmp,x_sub.T),(y-y_bar))
b = y_bar-torch.matmul(x_bar_tran,w)
model.params['b'] = b
model.params['w'] = torch.squeeze(w,dim=-1)
return model2.5 基于线性回归的波士顿房价预测
2.5.1 数据处理
2.5.1.1 数据集介绍
import pandas as pd # 开源数据分析和操作工具
# 利用pandas加载波士顿房价的数据集
data=pd.read_csv("boston_house_prices.csv")
# 预览前5行数据
print(data.head()) CRIM ZN INDUS CHAS NOX ... RAD TAX PTRATIO LSTAT MEDV
0 0.00632 18.0 2.31 0 0.538 ... 1 296 15.3 4.98 24.0
1 0.02731 0.0 7.07 0 0.469 ... 2 242 17.8 9.14 21.6
2 0.02729 0.0 7.07 0 0.469 ... 2 242 17.8 4.03 34.7
3 0.03237 0.0 2.18 0 0.458 ... 3 222 18.7 2.94 33.4
4 0.06905 0.0 2.18 0 0.458 ... 3 222 18.7 5.33 36.2
2.5.1.2 数据清洗
- 缺失值分析
# 查看各字段缺失值统计情况
print(data.isna().sum())CRIM 0
ZN 0
INDUS 0
CHAS 0
NOX 0
RM 0
AGE 0
DIS 0
RAD 0
TAX 0
PTRATIO 0
LSTAT 0
MEDV 0
dtype: int64
从输出结果看,波士顿房价预测数据集中不存在缺失值的情况。
- 异常值处理
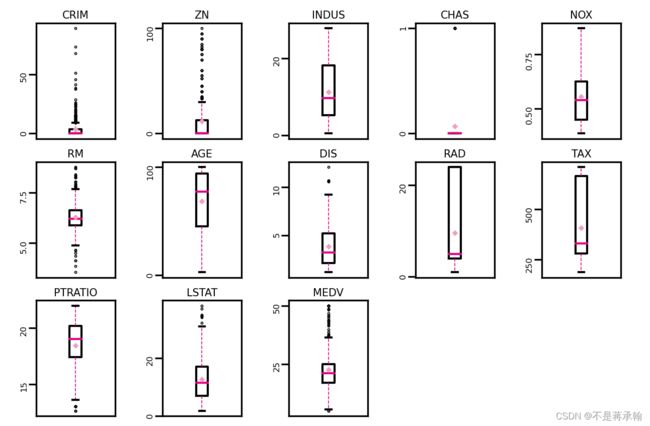
通过箱线图直观的显示数据分布,并观测数据中的异常值。箱线图一般由五个统计值组成:最大值、上四分位、中位数、下四分位和最小值。一般来说,观测到的数据大于最大估计值或者小于最小估计值则判断为异常值,其中
最大估计值=上四分位+1.5∗(上四分位−下四分位)
最小估计值=下四分位−1.5∗(上四分位−下四分位)
# 箱线图查看异常值分布
def boxplot(data, fig_name):
# 绘制每个属性的箱线图
data_col = list(data.columns)
# 连续画几个图片
plt.figure(figsize=(5, 5), dpi=300)
# 子图调整
plt.subplots_adjust(wspace=0.6)
# 每个特征画一个箱线图
for i, col_name in enumerate(data_col):
plt.subplot(3, 5, i + 1)
# 画箱线图
plt.boxplot(data[col_name],
showmeans=True,
meanprops={"markersize": 1, "marker": "D", "markeredgecolor": '#f19ec2'}, # 均值的属性
medianprops={"color": '#e4007f'}, # 中位数线的属性
whiskerprops={"color": '#e4007f', "linewidth": 0.4, 'linestyle': "--"},
flierprops={"markersize": 0.4},
)
# 图名
plt.title(col_name, fontdict={"size": 5}, pad=2)
# y方向刻度
plt.yticks(fontsize=4, rotation=90)
plt.tick_params(pad=0.5)
# x方向刻度
plt.xticks([])
plt.savefig(fig_name)
plt.show()
boxplot(data, 'ml-vis5.pdf')
从输出结果看,数据中存在较多的异常值(图中上下边缘以外的空心小圆圈)。
使用四分位值筛选出箱线图中分布的异常值,并将这些数据视为噪声,其将被临界值取代,代码实现如下:
# 四分位处理异常值
num_features = data.select_dtypes(exclude=['object', 'bool']).columns.tolist()
for feature in num_features:
if feature == 'CHAS':
continue
Q1 = data[feature].quantile(q=0.25) # 下四分位
Q3 = data[feature].quantile(q=0.75) # 上四分位
IQR = Q3 - Q1
top = Q3 + 1.5 * IQR # 最大估计值
bot = Q1 - 1.5 * IQR # 最小估计值
values = data[feature].values
values[values > top] = top # 临界值取代噪声
values[values < bot] = bot # 临界值取代噪声
data[feature] = values.astype(data[feature].dtypes)
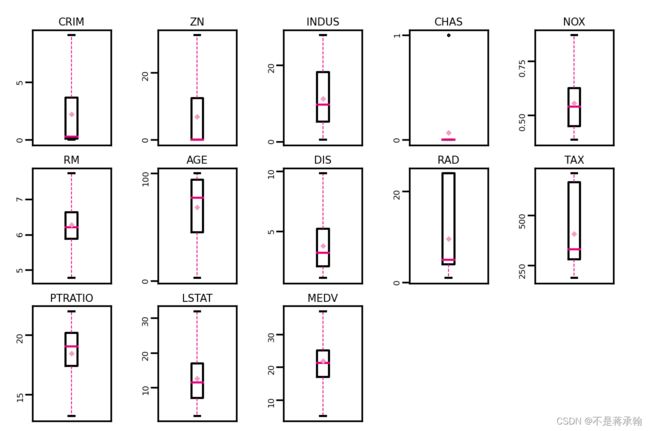
# 再次查看箱线图,异常值已被临界值替换(数据量较多或本身异常值较少时,箱线图展示会不容易体现出来)
boxplot(data, 'ml-vis6.pdf')从输出结果看,经过异常值处理后,箱线图中异常值得到了改善。
2.5.1.3 数据集划分
由于本实验比较简单,将数据集划分为两份:训练集和测试集,不包括验证集。
具体代码如下:
import torch
torch.manual_seed(10)
# 划分训练集和测试集
def train_test_split(X, y, train_percent=0.8):
n = len(X)
shuffled_indices = torch.randperm(n) # 返回一个数值在0到n-1、随机排列的1-D Tensor
train_set_size = int(n * train_percent)
train_indices = shuffled_indices[:train_set_size]
test_indices = shuffled_indices[train_set_size:]
X = X.values
y = y.values
X_train = X[train_indices]
y_train = y[train_indices]
X_test = X[test_indices]
y_test = y[test_indices]
return X_train, X_test, y_train, y_test
X = data.drop(['MEDV'], axis=1)
y = data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y) # X_train每一行是个样2.5.1.4 特征工程
为了消除纲量对数据特征之间影响,在模型训练前,需要对特征数据进行归一化处理,将数据缩放到[0, 1]区间内,使得不同特征之间具有可比性。
代码实现如下:
#特征工程
X_train = torch.tensor(X_train,dtype=torch.float32)
X_test = torch.tensor(X_test,dtype=torch.float32)
y_train = torch.tensor(y_train,dtype=torch.float32)
y_test = torch.tensor(y_test,dtype=torch.float32)
X_min = torch.min(X_train,dim=0)[0]
X_max = torch.max(X_train,dim=0)[0]
X_train = (X_train-X_min)/(X_max-X_min)
X_test = (X_test-X_min)/(X_max-X_min)
# 训练集构造
train_dataset=(X_train,y_train)
# 测试集构造
test_dataset=(X_test,y_test)得到X_min与X_max后,进行X_train-X_min时,会出现如下报错
TypeError: unsupported operand type(s) for -: 'Tensor' and 'torch.return_type
原因是X_min类型为torch.return_types.min(values和indices的结合体),我们只需要value部分,所以将
X_min = torch.min(X_train,dim=0) X_max = torch.max(X_train,dim=0)
改为
X_min = torch.min(X_train,dim=0)[0] X_max = torch.max(X_train,dim=0)[0]
2.5.2 模型构建
实例化一个线性回归模型,特征维度为 12:
from op import Linear
import torch.nn as nn
# 模型实例化
input_size = 12
model=Linear(input_size)
mse_loss = nn.MSELoss()2.5.4 模型训练
在组装完成Runner之后,我们将开始进行模型训练、评估和测试。首先,我们先实例化Runner,然后开始进行装配训练环境,接下来就可以开始训练了,相关代码如下:
# 模型保存文件夹
saved_dir = './models'
from Runner import Runner
from opitimizer import optimizer_lsm
optimizer = optimizer_lsm
# 实例化Runner
runner = Runner(model, optimizer=optimizer,loss_fn=None, metric=mse_loss)
# 启动训练
runner.train(train_dataset,reg_lambda=0,model_dir=saved_dir)打印出训练得到的权重:
columns_list = data.columns.to_list()
weights = runner.model.params['w'].tolist()
b = runner.model.params['b'].item()
for i in range(len(weights)):
print(columns_list[i],"weight:",weights[i])
print("b:",b)
CRIM weight: -5.261089324951172
ZN weight: 1.362697958946228
INDUS weight: -0.024794816970825195
CHAS weight: 1.8001978397369385
NOX weight: -7.556751251220703
RM weight: 9.557075500488281
AGE weight: -1.3511643409729004
DIS weight: -9.96794605255127
RAD weight: 7.528500556945801
TAX weight: -5.0824761390686035
PTRATIO weight: -6.9966583251953125
LSTAT weight: -13.183669090270996
b: 32.6215934753418
2.5.5 模型测试
# 加载模型权重
runner.load_model(saved_dir)
mse = runner.evaluate(test_dataset)
print('MSE:', mse.item())MSE: 11.210776329040527
2.5.6 模型预测
runner.load_model(saved_dir)
pred = runner.predict(X_test[:1])
print("真实房价:",y_test[:1].item())
print("预测的房价:",pred.item())真实房价: 18.899999618530273
预测的房价: 21.52915382385254
问题1:
使用类实现机器学习模型的基本要素有什么优点?
- 方便复用(如果你用函数写,就要复制整块代码,增加了代码量,增加了出错率)
- 方便扩展(函数写段代码,若要升级、扩展,都十分复杂,容易出错,用类来扩展,则方便清晰)
- 方便维护(因为类是把抽象的东西映射成我们常见的,摸得到的东西,容易理解,维护也方便)
问题2:
算子op、优化器opitimizer放在单独的文件中,主程序在使用时调用该文件。这样做有什么优点?
不用再复制粘贴一边该函数,节省时间,程序更简洁
作业1:
线性回归通常使用平方损失函数,能否使用交叉熵损失函数?为什么?
1、直观理解
从平方损失函数运用到多分类场景下,可知平方损失函数对每一个输出结果都十分看重,而交叉熵损失函数只对正确分类的结果看重。例如,对于一个多分类模型其模型结果输出为(a,b,c),而实际真实结果为(1,0,0)。则根据两种损失函数的定义其损失函数可以描述为:
![]()
![]()
从上述的结果中可以看出,交叉熵损失函数只和分类正确的预测结果有关。而平方损失函数还和错误的分类有关,该损失函数除了让正确分类尽量变大,还会让错误分类都变得更加平均,但实际中后面的这个调整使没必要的。但是对于回归问题这样的考虑就显得重要了,因而回归问题上使用交叉熵并不适合。
2、理论角度分析
平方数损失函数假设最终结果都服从高斯分布,而高斯分布实际上是一个连续变量,并不是一个离散变量。如果假设结果变量服从均值![]() ,方差为
,方差为![]() ,那么利用最大似然法就可以优化它的负对数似然,公式最终变为了:
,那么利用最大似然法就可以优化它的负对数似然,公式最终变为了:
除去与y无关的项目,最后剩下的就是平方损失函数的形式。
作业2:
对于一个三分类问题,数据集的真实标签和模型的预测标签如下:
真实标签 1 1 2 2 2 3 3 3 3
预测标签 1 2 2 2 3 3 3 1 2
分别计算模型的精确率、召回率、F1值以及它们的宏平均和微平均
精确率:
![]()
![]()
![]()
召回率:
![]()
![]()
![]()
F值:![]() 一般取值为1
一般取值为1
![]()
![]()
![]()
宏平均:
微平均:
心得体会:
将算子从理论应用到了实践,也第一次调用py文件使用函数,以前都是把所有代码放到一个文件里,经常写代码写着写着就眼花耳鸣,手忙脚乱,脑袋发晕,这次接触到了直接调用py文件后,代码变得更加整洁。
关于对象和类的用法,因为当初java没学好,所以现在对封装类的学习很吃力。对于线性回归模型的评估,我MSE的值非常大,但是最后w和b的值都很接近真实值,调试了好多遍都没找出问题,我怀疑就是我Linear类的使用有问题,我接下来有时间还会继续找出问题根源。
关于多项式回归,当我们使用多项式去拟合散点时,需要确定两个要素,分别是:多项式系数 w 以及多项式阶数 m,这也是多项式的两个基本要素。当然也可以手动指定多项式的阶数m的大小,这样就只需要确定系数w的值了。
波士顿房价预测中,了解到了箱线图异常处理。直接使用Runner类去进行模型训练,将学习过程规范化。
机器学习不是依赖自身而发展起来的,而是站在了诸多巨人的肩膀之上。这次实验还是借鉴诸多邱老师的代码,即使是现成的代码摆在那,把代码理解透依然是一个艰难的过程,而且实验内容好多,我感觉我不是在巨人肩膀上,我像沉在大海里快要窒息。






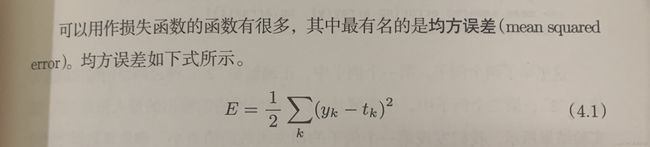
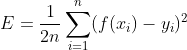





![=max\sum_{i}^{N}[-\frac{1}{2}log(2\pi\sigma^{2} )-\frac{(t_{i}-y)}{2\sigma^{2}}]](http://img.e-com-net.com/image/info8/988080aa23d349a0bbe32a880a817369.gif)