线性回归的数据维度解释,softmax回归、交叉熵损失函数及手工实现_FashionMNIST数据集
一、线性回归与Softmax回归
在上一篇线性回归原理及手工实现实现了一层简单的线性回归模型。对于一层简单的Softmax回归模型,可以在线性回归模型输出的基础上再套一层Softmax函数,输出每个类别的概率。
对于一层线性回归模型,网络预测的输出 Y ^ \hat{Y} Y^如下所示,其中 X ∈ R n × d X\in{R}^{ n\times d} X∈Rn×d, W ∈ R d × q W\in{R}^{ d\times q} W∈Rd×q, b ∈ R 1 × q b\in{R}^{1\times q} b∈R1×q, O ∈ R n × q O\in{R}^{n\times q} O∈Rn×q, Y ^ ∈ R n × q \hat{Y}\in{R}^{n\times q} Y^∈Rn×q, n n n为该批次样本个数, d d d为特征维度, q q q为最终标签的类别个数: O = X W + b O=XW+b O=XW+b Y ^ = O \hat{Y}=O Y^=O对于一层Softmax回归模型,网络预测的输出 Y ^ \hat{Y} Y^: Y ^ = S o f t m a x ( O ) \hat{Y}=Softmax(O) Y^=Softmax(O)
1、单个样本 x ( i ) x^{(i)} x(i)的线性回归过程
在小批量样本学习时,每批有 n n n个样本,对于某个样本 x ( i ) x^{(i)} x(i),有 d d d个特征 x 1 ( i ) , x 2 ( i ) , . . . , x d ( i ) x^{(i)}_1,x^{(i)}_2,...,x^{(i)}_d x1(i),x2(i),...,xd(i),进行线性回归时, o ( i ) o^{(i)} o(i)应有 q q q个输出 o 1 ( i ) , o 2 ( i ) , . . . , o q ( i ) o^{(i)}_1,o^{(i)}_2,...,o^{(i)}_q o1(i),o2(i),...,oq(i),预测输出 y ^ ( i ) = s o f t m a x ( o ( i ) ) \hat y^{(i)}=softmax(o^{(i)}) y^(i)=softmax(o(i)),每个输出 y ^ ( i ) \hat y^{(i)} y^(i)为对应类别的概率, q q q个概率的总和为1。下图为单个样本 x ( i ) x^{(i)} x(i)的线性回归过程,还没有进行 y ^ ( i ) = s o f t m a x ( o ( i ) ) \hat y^{(i)}=softmax(o^{(i)}) y^(i)=softmax(o(i))运算。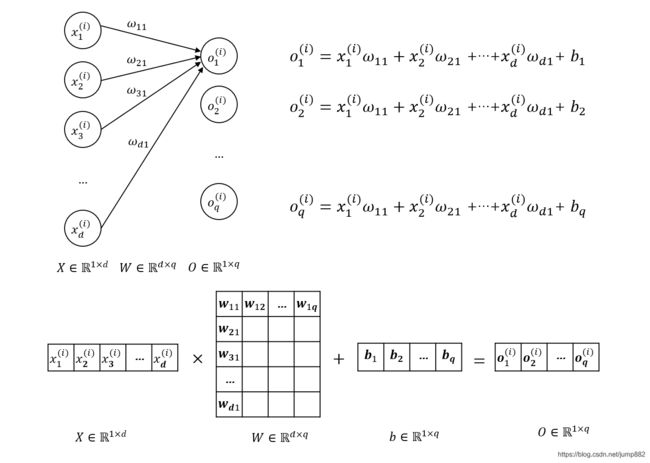
2、小批量样本 x ( i ) x^{(i)} x(i)的线性回归过程
对于单个样本,权重矩阵 W , b W,b W,b是维度不变的。
 也就是说假设数据集中有60000条样本数据,那要学习的权重矩阵还是 W , b W,b W,b,只是在每次使用梯度下降法更新 W , b W,b W,b的时候不再是一条样本一条样本地更新,使用小批量样本计算,可以借助矩阵乘法加快计算速度。
也就是说假设数据集中有60000条样本数据,那要学习的权重矩阵还是 W , b W,b W,b,只是在每次使用梯度下降法更新 W , b W,b W,b的时候不再是一条样本一条样本地更新,使用小批量样本计算,可以借助矩阵乘法加快计算速度。
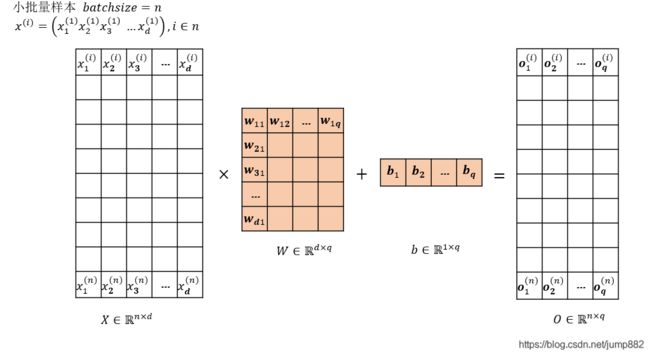 线性回归的输出结果以矩阵形式表达如下所示,其中 X ∈ R n × d X\in{R}^{ n\times d} X∈Rn×d, W ∈ R d × q W\in{R}^{ d\times q} W∈Rd×q, b ∈ R 1 × q b\in{R}^{1\times q} b∈R1×q, O ∈ R n × q O\in{R}^{n\times q} O∈Rn×q, Y ^ ∈ R n × q \hat{Y}\in{R}^{n\times q} Y^∈Rn×q, n n n为该批次样本个数, d d d为特征维度, q q q为最终标签的类别个数: O = X W + b O=XW+b O=XW+b
线性回归的输出结果以矩阵形式表达如下所示,其中 X ∈ R n × d X\in{R}^{ n\times d} X∈Rn×d, W ∈ R d × q W\in{R}^{ d\times q} W∈Rd×q, b ∈ R 1 × q b\in{R}^{1\times q} b∈R1×q, O ∈ R n × q O\in{R}^{n\times q} O∈Rn×q, Y ^ ∈ R n × q \hat{Y}\in{R}^{n\times q} Y^∈Rn×q, n n n为该批次样本个数, d d d为特征维度, q q q为最终标签的类别个数: O = X W + b O=XW+b O=XW+b
3、Softmax回归过程
根据上述推导, O ∈ R n × q O\in{R}^{n\times q} O∈Rn×q,最终预测结果 Y ^ ∈ R n × q \hat{Y}\in{R}^{n\times q} Y^∈Rn×q, n n n个样本,每个样本都有 q q q个概率,这 q q q个概率中最大值对应的标签,就是最终的输出类别: Y ^ = S o f t m a x ( O ) \hat{Y}=Softmax(O) Y^=Softmax(O)对于第 i i i个样本的预测 y ^ ( i ) = ( y ^ 1 ( i ) , y ^ 2 ( i ) , . . . , y ^ q ( i ) ) \hat y^{(i)}=(\hat y_1^{(i)},\hat y_2^{(i)} ,...,\hat y_q^{(i)} ) y^(i)=(y^1(i),y^2(i),...,y^q(i))。其中 y ^ 1 ( i ) = e x p ( o 1 ( i ) ) ∑ k = 1 q e x p ( o k ( i ) ) , y ^ 2 ( i ) = e x p ( o 2 ( i ) ) ∑ k = 1 q e x p ( o k ( i ) ) , . . . , y ^ q ( i ) = e x p ( o q ( i ) ) ∑ k = 1 q e x p ( o k ( i ) ) \hat y_1^{(i)}=\frac{exp(o_1^{(i)})}{\sum_{k=1}^qexp(o_k^{(i)})},\hat y_2^{(i)}=\frac{exp(o_2^{(i)})}{\sum_{k=1}^qexp(o_k^{(i)})},...,\hat y_q^{(i)}=\frac{exp(o_q^{(i)})}{\sum_{k=1}^qexp(o_k^{(i)})} y^1(i)=∑k=1qexp(ok(i))exp(o1(i)),y^2(i)=∑k=1qexp(ok(i))exp(o2(i)),...,y^q(i)=∑k=1qexp(ok(i))exp(oq(i))
# 假设线性回归后,有10个样本,共3个类别(q=3)
# softmax计算后,每个样本的3个类别概率之和为1。
output = torch.randn([10,3],dtype=torch.float32)
def my_softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition
y_hat = my_softmax(output)
print(output)
print(y_hat)
tensor([[ 1.7054, -0.7565, 0.1639],
[-0.9732, -0.9422, 1.0874],
[-0.2228, 0.5962, -0.2224],
[ 0.8227, 0.4886, -0.0543],
[-2.0010, -0.9472, -1.4959],
[-0.1829, 0.3492, -0.0258],
[ 1.2977, -2.2332, -1.0000],
[ 0.0841, 0.0186, 1.2358],
[ 0.2671, 0.4318, -0.0222],
[ 1.1387, 1.4518, -0.7576]])
tensor([[0.7696, 0.0656, 0.1647],
[0.1012, 0.1044, 0.7944],
[0.2343, 0.5314, 0.2344],
[0.4690, 0.3358, 0.1951],
[0.1810, 0.5191, 0.2999],
[0.2582, 0.4396, 0.3022],
[0.8851, 0.0259, 0.0889],
[0.1961, 0.1836, 0.6203],
[0.3415, 0.4027, 0.2558],
[0.3972, 0.5432, 0.0596]])
4、交叉熵损失函数
1)二分类
共 N N N个样本,总 L o s s Loss Loss值为所有样本的 L o s s ( i ) Loss^{(i)} Loss(i)均值: L o s s = 1 N ∑ i = 1 N L o s s ( i ) Loss=\frac{1}{N}\sum_{i=1}^NLoss^{(i)} Loss=N1i=1∑NLoss(i) L o s s ( i ) = − [ y ( i ) ∗ l o g ( y ^ ( i ) ) + ( 1 − y ( i ) ) ∗ l o g ( 1 − y ^ ( i ) ) ] Loss^{(i)}=-[y^{(i)}*log(\hat y^{(i)})+(1-y^{(i)})*log(1-\hat y^{(i)})] Loss(i)=−[y(i)∗log(y^(i))+(1−y(i))∗log(1−y^(i))]单个样本 L o s s ( i ) Loss^{(i)} Loss(i)计算过程如上所示。要注意区分 y ( i ) y^{(i)} y(i)以及 y ^ ( i ) \hat y^{(i)} y^(i): y ( i ) y^{(i)} y(i)是真实的标签,只能取值0或1。 y ^ ( i ) \hat y^{(i)} y^(i)是经过 s o f t m a x softmax softmax函数预测出的概率。
# y是真实标签,只有0、1两类
# y_hat是经过softmax函数输出的0、1两类各自的概率
def my_softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition
def loss_crossentropy(predict, y):
find = torch.zeros(predict.shape[0])
for id, item in enumerate(predict):
ture_y = int(y[id])
temp = item[ture_y]
find[id] = -torch.log(temp)
return find
output = torch.randn([5,2],dtype=torch.float32)
y = torch.tensor([0., 1., 1., 1., 0.])
y_hat = my_softmax(output)
loss = loss_crossentropy(y_hat, y)
print('output:\n', output)
print('y_hat:\n', y_hat)
print('y:', y)
print('loss:',loss, '\nloss_sum:',loss.sum())
output:
tensor([[ 0.8984, 0.7033],
[-1.0901, 1.1588],
[ 0.1273, -0.6588],
[-0.1923, -0.0615],
[-2.2441, -0.0696]])
y_hat:
tensor([[0.5486, 0.4514],
[0.0955, 0.9045],
[0.6870, 0.3130],
[0.4673, 0.5327],
[0.1021, 0.8979]])
y: tensor([0., 1., 1., 1., 0.])
loss: tensor([0.6003, 0.1003, 1.1615, 0.6299, 2.2822])
loss_sum: tensor(4.7742)
2)多分类
共 N N N个样本,总 L o s s Loss Loss值为所有样本的 L o s s ( i ) Loss^{(i)} Loss(i)均值: L o s s = 1 N ∑ i = 1 N L o s s ( i ) Loss=\frac{1}{N}\sum_{i=1}^NLoss^{(i)} Loss=N1i=1∑NLoss(i) L o s s ( i ) = − ∑ k = 1 q y k ( i ) ∗ l o g ( y ^ k ( i ) ) Loss^{(i)}=-\sum_{k=1}^{q}y_k^{(i)}*log(\hat y_k^{(i)}) Loss(i)=−k=1∑qyk(i)∗log(y^k(i))单个样本 L o s s ( i ) Loss^{(i)} Loss(i)计算过程如上所示。要注意区分 y k ( i ) y_k^{(i)} yk(i)以及 y ^ k ( i ) \hat y_k^{(i)} y^k(i): y k ( i ) y_k^{(i)} yk(i)是真实的标签对应类别,是第 k k k类就取值为1,否则为0,会有很多项为0被屏蔽掉不参与计算。 y ^ k ( i ) \hat y_k^{(i)} y^k(i)是经过 s o f t m a x softmax softmax函数预测出的概率。也就是说,交叉熵损失函数只关心正确标签对应的概率取值为多少,这个概率值越大,就越能保证能够正确分类结果。
# 延续使用上面定义的 my_softmax(X)、loss_crossentropy(predict, y)
# 5个样本,有3个类别的多分类交叉熵损失函数计算
output = torch.randn([5,3],dtype=torch.float32)
y = torch.tensor([2., 1., 2., 0., 0.])
y_hat = my_softmax(output)
loss = loss_crossentropy(y_hat, y)
print('output:\n', output)
print('y_hat:\n', y_hat)
print('y:', y)
print('loss:',loss, '\nloss_sum:',loss.sum())
output:
tensor([[ 1.3562, -0.6458, -1.0921],
[ 0.2846, -0.8920, -0.6023],
[-0.1979, 1.8874, -0.4902],
[-2.1545, -1.3481, -0.2012],
[-0.7509, 1.2623, 0.2108]])
y_hat:
tensor([[0.8187, 0.1106, 0.0708],
[0.5813, 0.1792, 0.2395],
[0.1021, 0.8217, 0.0762],
[0.0972, 0.2176, 0.6852],
[0.0901, 0.6743, 0.2356]])
y: tensor([2., 1., 2., 0., 0.])
loss: tensor([2.6483, 1.7190, 2.5741, 2.3313, 2.4073])
loss_sum: tensor(11.6800)
二、Softmax回归手工实现——FashionMNIST数据集分类
import torch
import torchvision
import random
from torch.utils import data
from torchvision import transforms
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="./data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="./data", train=False, transform=trans, download=True)
num_inputs = 784
num_outputs = 10
batch_size = 256
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=0)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=10000, shuffle=False, num_workers=0)
def my_softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition
def loss_crossentropy(predict, y):
find = torch.zeros(predict.shape[0])
for id, item in enumerate(predict):
ture_y = int(y[id])
temp = item[ture_y]
find[id] = -torch.log(temp)
return find
def model(params, X, y):
#return torch.softmax(torch.matmul(X.reshape((-1, w.shape[0])), w) + b, dim=1) 使用pytorch softmax
return my_softmax(torch.matmul(X.reshape((-1, w.shape[0])), w) + b)
def loss_crossentropy(predict, y):
find = torch.zeros(predict.shape[0])
for id, item in enumerate(predict):
ture_y = int(y[id])
temp = item[ture_y]
find[id] = -torch.log(temp)
return find
def sgd(params, lr, batch_size):
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
epochs = 10
w = torch.normal(0, 0.01, size=(num_inputs,num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
lr = 0.1
for epoch in range(epochs):
for X, y in train_iter:
predict = model([w,b], X, y)
loss = loss_crossentropy(predict, y)
loss.sum().backward() # 计算梯度
sgd([w, b], lr, batch_size) # 更新参数值
with torch.no_grad():
for X, y in test_iter:
predict = model([w, b], X, y)
test_loss = loss_crossentropy(predict, y)
predict_class = torch.argmax(predict, dim=1)
cmp = predict_class == y
print(f'epoch {epoch + 1}, train_loss {float(loss.mean()):f}, test_loss {float(test_loss.mean()):f}, test_acc {float(cmp.sum()) / 10000.}')
epoch 1, train_loss 0.740523, test_loss 0.626370, test_acc 0.7914
epoch 2, train_loss 0.636658, test_loss 0.564578, test_acc 0.809
epoch 3, train_loss 0.376184, test_loss 0.535320, test_acc 0.8177
epoch 4, train_loss 0.334157, test_loss 0.516010, test_acc 0.8243
epoch 5, train_loss 0.343276, test_loss 0.507193, test_acc 0.8273
epoch 6, train_loss 0.400475, test_loss 0.507105, test_acc 0.8246
epoch 7, train_loss 0.502912, test_loss 0.490121, test_acc 0.8315
epoch 8, train_loss 0.537717, test_loss 0.484207, test_acc 0.8329
epoch 9, train_loss 0.617670, test_loss 0.478643, test_acc 0.8332
epoch 10, train_loss 0.316625, test_loss 0.475598, test_acc 0.8357