K-means原理与算法改进及其python实现
K-means入门学习
- 一、算法概述
- 二、算法思想
- 三、算法实现步骤
- 四、算法图解
- 五、算法优缺点
- 六、k-means算法python实现
-
- 6.1 sklearn聚类
- 6.2 各省份消费数据聚类
- 6.3 常规方法python实现
- 七、相关参数调整
- 八、优化算法K-means++
-
- 8.1 kmeans不足之处
- 8.2 kmeans++
- 8.3 层次聚类
一、算法概述
K-means聚类算法也称k均值聚类算法,是集简单和经典于一身的基于距离的聚类算法。它采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
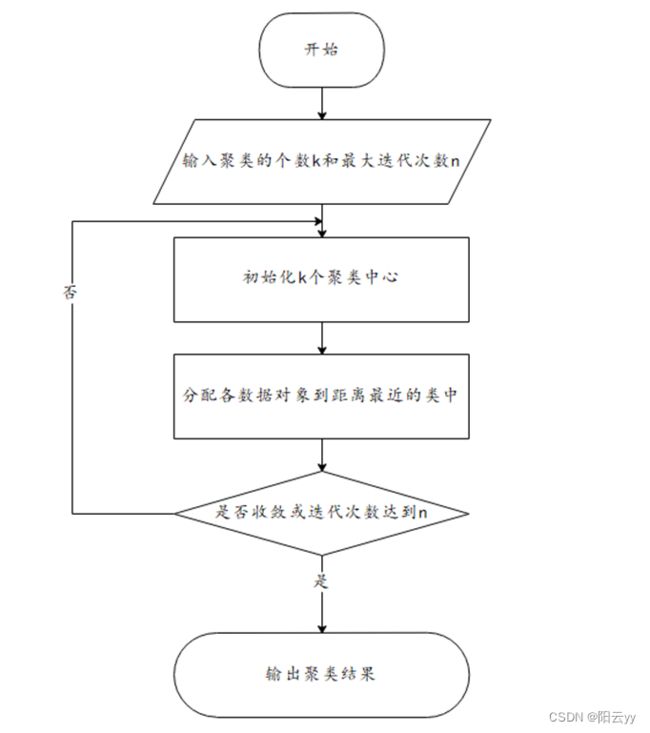
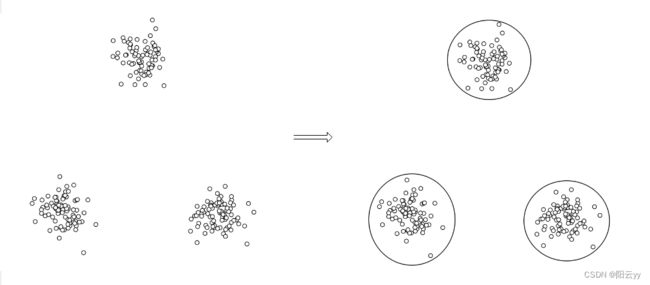
K-Means算法主要解决的问题如下图所示。我们可以看到,在图的左边有一些点,我们可以看出来有三个点群,但是我们怎么才能将三个点群分为图右边的三个集群,这就是k-means算法能够解决的问题。
二、算法思想
K-means聚类算法是一种迭代求解的聚类分析算法,其步骤是随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。
三、算法实现步骤
- 指定需要划分的簇的个数K值(类的个数);
- 随机地选择K个数据对象作为初始的聚类中心(不一定要是我们的样本点,可以随机生成)
- 计算其余的各个数据对象到这K个初始聚类中心的距离,把数据对象划归到距离它最近的那个中心所处在的簇类中
- 调整新类并且重新计算出新类的中心(每个新集合质心)
- 循环步骤三和四,看中心是否收敛(不变),如果收敛或达到迭代次数则停止循环
四、算法图解
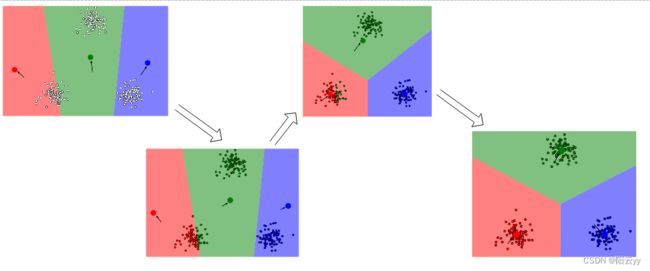
首先随机选择三个聚类中心;然后重复调整聚类中心位置;最终收敛,形成三个簇。
五、算法优缺点
优点:
- 对处理大数据集,该算法是相对高效率的。
- 原理比较简单,实现也是很容易,收敛速度快。
- 当结果簇是密集的,而簇与簇之间区别明显时, 它的效果较好。
- 主要需要调参的参数仅仅是簇数k。
缺点:
- 要求用户必须事先给出要生成的簇的数目K。
- K值需要预先给定,很多情况下K值的估计是非常困难的。
- K-Means算法对初始选取的质心点是敏感的,不同的随机种子点得到的聚类结果完全不同 ,对结果影响很大。
- 对噪音和异常点比较的敏感。用来检测异常值。
- 采用迭代方法,可能只能得到局部的最优解,而无法得到全局的最优解。
六、k-means算法python实现
6.1 sklearn聚类
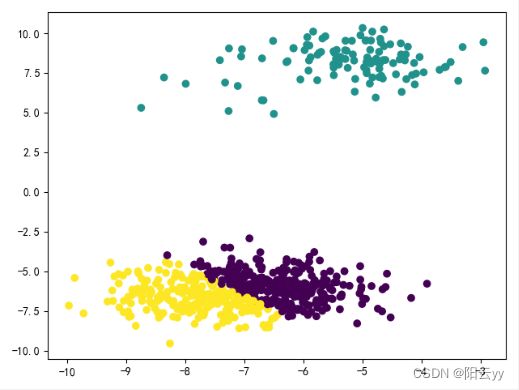
make_blobs函数是为聚类产生数据集,产生一个数据集和相应的标签
make_blobs方法:
sklearn.datasets.make_blobs(n_samples=100,n_features=2,centers=3, cluster_std=1.0,center_box=(-10.0,10.0),shuffle=True,random_state=None)
n_samples:表示数据样本点个数,默认值100
n_features:是每个样本的特征(或属性)数,也表示数据的维度,默认值是2
centers:表示类别数(标签的种类数),默认值3
cluster_std:表示每个类别的方差,例如我们希望生成2类数据,其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0,3.0],浮点数或者浮点数序列,默认值1.0
center_box:中心确定之后的数据边界,默认值(-10.0, 10.0)
shuffle:将数据进行洗乱,默认值是True
random_state:官网解释是随机生成器的种子,可以固定生成的数据,给定数之后,每次生成的数据集就是固定的。若不给定值,则由于随机性将导致每次运行程序所获得的的结果可能有所不同。在使用数据生成器练习机器学习算法练习或python练习时建议给定数值。- 生成数据
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
#参数:
# n_samples=100 样本数量
# n_features=2 特征数量
# centers=3 中心点
#返回值:
# X_train: 测试集
# y_train: 特征值
X_train,y_train = make_blobs(n_samples=100, n_features=2, centers=3)
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)
plt.show()
#参数
# n_clusters 将预测结果分为几簇
kmeans = KMeans(n_clusters=3) # 获取模型
kmeans.fit(X_train) #这里不需要给他答案 只把要分类的数据给他 即可
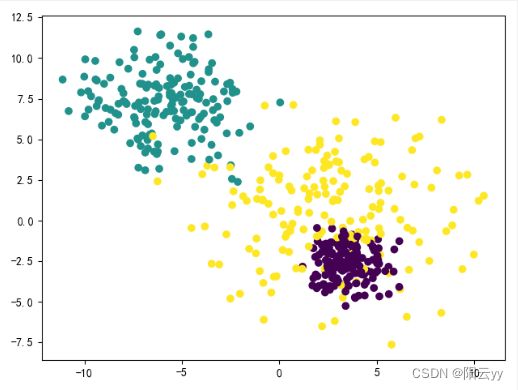
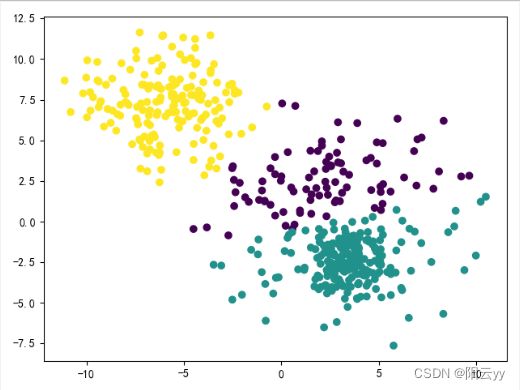
- 预测
predict_y = kmeans.predict(X_train)
plt.scatter(X_train[:,0],X_train[:,1],c=predict_y) #预测结果
plt.show()
6.2 各省份消费数据聚类
- 导入数据
from sklearn.cluster import KMeans
import pandas as pd
df = pd.read_excel('data.xlsx',sheet_name="人均消费(元)")
data = df.iloc[:,1:]
print(data)
数据显示:
食品 衣着 家庭设备 医疗 交通 娱乐 居住 杂项
0 2959.19 730.79 749.41 513.34 467.87 1141.82 478.42 457.64
1 2459.77 495.47 697.33 302.87 284.19 735.97 570.84 305.08
2 1495.63 515.90 362.37 285.32 272.95 540.58 364.91 188.63
3 1406.33 477.77 290.15 208.57 201.50 414.72 281.84 212.10
4 1303.97 524.29 254.83 192.17 249.81 463.09 287.87 192.96
5 1730.84 553.90 246.91 279.81 239.18 445.20 330.24 163.86
6 1561.86 492.42 200.49 218.36 220.69 459.62 360.48 147.76
7 1410.11 510.71 211.88 277.11 224.65 376.82 317.61 152.85
8 3712.31 550.74 893.37 346.93 527.00 1034.98 720.33 462.03
9 2207.58 449.37 572.40 211.92 302.09 585.23 429.77 252.54
10 2629.16 557.32 689.73 435.69 514.66 795.87 575.76 323.36
11 1844.78 430.29 271.28 126.33 250.56 513.18 314.00 151.39
12 2709.46 428.11 334.12 160.77 405.14 461.67 535.13 232.29
13 1563.78 303.65 233.81 107.90 209.70 393.99 509.39 160.12
14 1675.75 613.32 550.71 219.79 272.59 599.43 371.62 211.84
15 1427.65 431.79 288.55 208.14 217.00 337.76 421.31 165.32
16 1942.23 512.27 401.39 206.06 321.29 697.22 492.60 226.45
17 1783.43 511.88 282.84 201.01 237.60 617.74 523.52 182.52
18 3055.17 353.23 564.56 356.27 811.88 873.06 1082.82 420.81
19 2033.87 300.82 338.65 157.78 329.06 621.74 587.02 218.27
20 2057.86 186.44 202.72 171.79 329.65 477.17 312.93 279.19
21 2303.29 589.99 516.21 236.55 403.92 730.05 438.41 225.80
22 1974.28 507.76 344.79 203.21 240.24 575.10 430.36 223.46
23 1673.82 437.75 461.61 153.32 254.66 445.59 346.11 191.48
24 2194.25 537.01 369.07 249.54 290.84 561.91 407.70 330.95
25 2646.61 839.70 204.44 209.11 379.30 371.04 269.59 389.33
26 1472.95 390.89 447.95 259.51 230.61 490.90 469.10 191.34
27 1525.57 472.98 328.90 219.86 206.65 449.69 249.66 228.19
28 1654.69 437.77 258.78 303.00 244.93 479.53 288.56 236.51
29 1375.46 480.89 273.84 317.32 251.08 424.75 228.73 195.93
30 1608.82 536.05 432.46 235.82 250.28 541.30 344.85 214.40
- 建立模型并训练数据
k=3
model = KMeans(n_clusters= k,init='k-means++')
clf = model.fit(data)
predict_y = clf.predict(data)
- 聚类结果
print(df[predict_y==0]['省份'])
print(df[predict_y==1]['省份'])
print(df[predict_y==2]['省份'])
结果显示:
2 河北
3 山西
4 内蒙古
5 辽宁
6 吉林
7 黑龙江
11 安徽
13 江西
14 山东
15 河南
17 湖北
23 贵州
26 陕西
27 甘肃
28 青海
29 宁夏
30 新疆
Name: 省份, dtype: object
1 天津
9 江苏
10 浙江
12 福建
16 湖南
19 广西
20 海南
21 重庆
22 四川
24 云南
25 西藏
Name: 省份, dtype: object
0 北京
8 上海
18 广东
Name: 省份, dtype: object
6.3 常规方法python实现
各城市消费水平聚类
import random
import pandas as pd
import numpy as np
#%%
# 计算欧拉距离
def calcDis(dataSet, centroids, k):
clalist = []
for data in dataSet:
diff = np.tile(data, (k, 1)) - centroids
squaredDiff = diff ** 2 # 平方
squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)
distance = squaredDist ** 0.5 # 开根号
clalist.append(distance)
clalist = np.array(clalist) # 返回一个每个点到质点的距离len(dateSet)*k的数组
return clalist
# 计算质心
def classify(dataSet, centroids, k):
# 计算样本到质心的距离
clalist = calcDis(dataSet, centroids, k)
# 分组并计算新的质心
minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标
newCentroids = pd.DataFrame(dataSet).groupby(
minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值
newCentroids = newCentroids.values
# 计算变化量
changed = newCentroids - centroids
return changed, newCentroids
# 使用k-means分类
def kmeans(dataSet, k):
# 随机取质心
# random.sample(list类型数据)
centroids = random.sample(list(dataSet), k)
# 更新质心 直到变化量全为0
changed, newCentroids = classify(dataSet, centroids, k)
while np.any(changed != 0):
changed, newCentroids = classify(dataSet, newCentroids, k)
centroids = sorted(newCentroids.tolist()) # tolist()将矩阵转换成列表 sorted()排序
# 根据质心计算每个集群
cluster = []
clalist = calcDis(dataSet, centroids, k) # 调用欧拉距离
minDistIndices = np.argmin(clalist, axis=1)
for i in range(k):
cluster.append([])
for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素
cluster[j].append(dataSet[i])
return centroids, cluster, minDistIndices
# 创建数据集
def createDataSet():
df = pd.read_excel(r"data.xlsx", sheet_name="人均消费(元)")
data = df.iloc[:, 1:]
return df,np.array(data)
if __name__ == '__main__':
df,dataSet = createDataSet()
centroids, cluster, minDist = kmeans(dataSet, 3)
print('质心为:%s' % centroids)
print('集群为:%s' % cluster)
print(df[minDist == 0]['省份'])
print(df[minDist == 1]['省份'])
print(df[minDist == 2]['省份'])
聚类结果:
2 河北
3 山西
4 内蒙古
5 辽宁
6 吉林
7 黑龙江
11 安徽
13 江西
14 山东
15 河南
17 湖北
23 贵州
26 陕西
27 甘肃
28 青海
29 宁夏
30 新疆
Name: 省份, dtype: object
1 天津
9 江苏
12 福建
16 湖南
19 广西
20 海南
21 重庆
22 四川
24 云南
25 西藏
Name: 省份, dtype: object
0 北京
8 上海
10 浙江
18 广东
Name: 省份, dtype: object
七、相关参数调整
以下程序来源链接: K均值算法
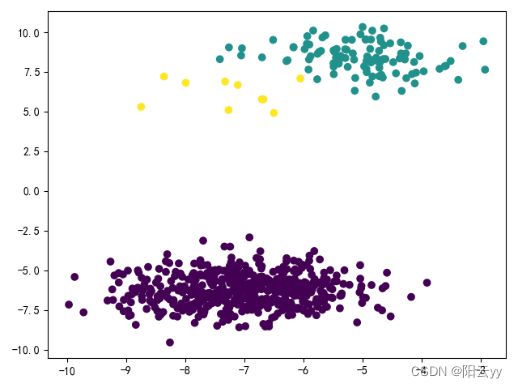
- 标准差
cluster_std不相同
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# cluster_std 各个中心的标准差
X_train,y_train = make_blobs(n_samples=500, n_features=2, centers=3, cluster_std=[1.0,2.0,3.0])
#参数
# n_clusters 将预测结果分为几簇
kmeans = KMeans(n_clusters=3) # 获取模型
kmeans.fit(X_train)
predict_y = kmeans.predict(X_train)
plt.scatter(X_train[:,0],X_train[:,1],c=y_train) # 原结果
plt.show()
plt.scatter(X_train[:,0],X_train[:,1],c=predict_y) #预测结果
plt.show()
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
# cluster_std 各个中心的标准差
X_train,y_train = make_blobs(n_samples=1500, n_features=2, centers=3)
# 创建训练集
X1 = X_train[y_train==0] # X1中的这些点 目标值都是0
X2 = X_train[y_train==1][:100] # X2中的这些点 目标值都是1
X3 = X_train[y_train==2][:10] # X3中的这些点 目标值都是2
# 将三个合为一个训练集
X_train = np.concatenate((X1,X2,X3))
# 创建结果集
# 前500个为0 再来100个1 再来10个2
y_train = [0]*500+[1]*100+[2]*10
plt.scatter(X_train[:,0],X_train[:,1],c=y_train) # 原结果
plt.show()
#参数
# n_clusters 将预测结果分为几簇
kmeans = KMeans(n_clusters=3) # 获取模型
kmeans.fit(X_train)
predict_y = kmeans.predict(X_train)
plt.scatter(X_train[:,0],X_train[:,1],c=predict_y) #预测结果
plt.show()
八、优化算法K-means++
8.1 kmeans不足之处
从 K m e a n s Kmeans Kmeans聚类算法的原理可知,在正式聚类之前首先需要完成的就是初始化 k k k个簇中心。使得收敛情况严重依赖于簇中心的初始化状况。如果在初始化过程中很不巧的将 k k k个(或大多数)簇中心都初始化了到同一个簇中,那么在这种情况下聚类算法很大程度上都不会收敛到全局最小值。也就是说,当簇中心初始化的位置不得当时,聚类结果将会出现严重的错误。
8.2 kmeans++
k-means++算法选择初始聚类中心的基本原则是:初始的聚类中心之间的相互距离要尽可能的远。
算法描述如下:
(只对K-means算法“初始化K个聚类中心” 这一步进行了优化)
- 随机选取一个样本作为第一个聚类中心;
- 计算每个样本与当前已有聚类中心的最短距离(即与最近一个聚类中心的距离),这个值越大,表示被选取作为聚类中心的概率较大;最后,用轮盘法(依据概率大小来进行抽选)选出下一个聚类中心;
- 重复步骤二,直到选出K个聚类中心。选出初始点后,就继续使用标准的K-means算法了。
程序实现:
def get_cent(points, k):
'''
kmeans++的初始化聚类中心的方法
:param points: 样本
:param k: 聚类中心的个数
:return: 初始化后的聚类中心
'''
m, n = np.shape(points)
cluster_centers = np.mat(np.zeros((k, n)))
# 1、随机选择一个样本点作为第一个聚类中心
index = np.random.randint(0, m)
cluster_centers[0, ] = np.copy(points[index, ]) # 复制函数,修改cluster_centers,不会影响points
# 2、初始化一个距离序列
d = [0.0 for i in range(m)]
for i in range(1, k):
sum_all = 0
for j in range(m):
# 3、对每一个样本找到最近的聚类中心点
d[j] = nearest(points[j, ], cluster_centers[0:i, ])
# 4、将所有的最短距离相加
sum_all += d[j]
# 5、取得sum_all之间的随机值
sum_all *= random()
# 6、获得距离最远的样本点作为聚类中心点
for j, di in enumerate(d): # enumerate()函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同事列出数据和数据下标一般用在for循环中
sum_all -= di
if sum_all > 0:
continue
cluster_centers[i] = np.copy(points[j, ])
break
return cluster_centers
8.3 层次聚类
参考来源:数学建模清风老师课件
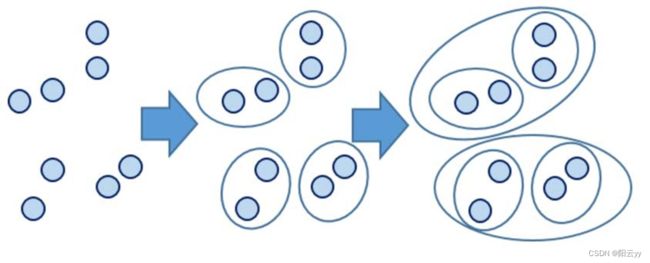
层次聚类的算法流程:
- 将每个对象看作一类,计算两两之间的最小距离;
- 将距离最小的两个类合并成一个新类;
- 重新计算新类与所有类之间的距离;
- 重复二三两步,直到所有类最后合并成一类;
# 调包
import matplotlib.pyplot as plt
import pandas as pd
import scipy.cluster.hierarchy as shc # 层次聚类
# 防止中文乱码
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
# 加载数据
df = pd.read_excel('data.xlsx',sheet_name="人均消费(元)")
print(df.head())
# 绘图
plt.figure(figsize=(16,10),dpi=100)
plt.title('省份消费数据聚类树状图',fontsize=22)
dend = shc.dendrogram(shc.linkage(df[['食品','衣着','家庭设备','医疗','交通','娱乐','居住','杂项']],
method='ward'),labels=df['省份'].values,color_threshold=100)
plt.xticks(fontsize=12)
plt.savefig('树状图.png') # 保存图片
plt.show()
本文为学习过程记录,根据学习情况继续更新。