贝叶斯分类器详解 从零开始 从理论到实践
贝叶斯分类器详解 从零开始 从理论到实践
- 大纲总览
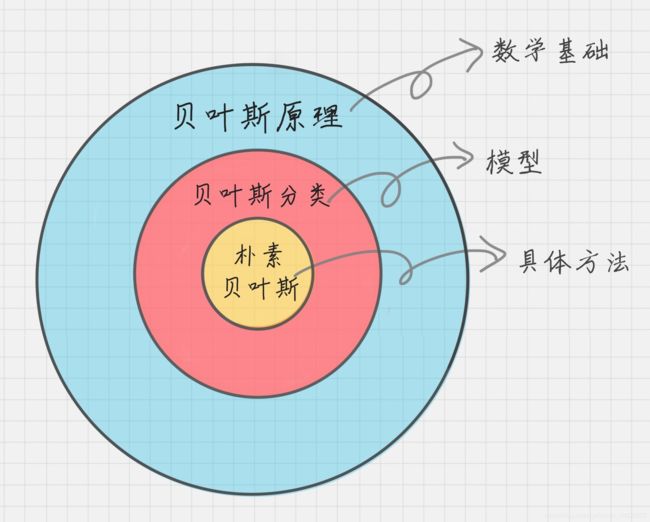
- 一、贝叶斯相关概念
-
- 1.1、频率学派和贝叶斯学派
-
- 1.1.1、频率学派
- 1.1.2、贝叶斯学派
- 1.2、概率论基础知识
- 1.3、贝叶斯定理
- 二、概率的分布
-
- 2.1、离散概率分布
-
- 2.1.1、伯努利分布(Bernoulli Distribution)
- 2.1.2、分类分布(Categorical Distribution)
- 2.1.3、二项分布(Binomial Distribution)
- 2.1.4 多项分布(Multinomial Distribution)
- 2.2、连续概率分布
-
- 2.2.1、正态分布(Normal Distribution)
- 2.2.2、贝塔分布(Beta Distribution)
- 三、贝叶斯分类
-
- 3.1、贝叶斯决策理论
- 3.2、参数估计
-
- 3.2.1、极大似然估计(Maximum Likelihood Estimation)
- 3.2.2、极大后验估计(Maximum A Posteriori Estimation)
- 3.3、朴素贝叶斯
-
- 3.3.1、模型的计算
- 3.3.2、模型的应用流程
- 3.3.3、模型的特点
- 3.3.4、模型的使用案例
-
- Laplace拉普拉斯修正
- 3.3.5、在Python中使用朴素贝叶斯分类算法
-
- 3.3.5.1 伯努利朴素贝叶斯
- 3.3.5.2 多项式朴素贝叶斯
- 3.3.5.3 高斯朴素贝叶斯
- 3.3.5.4 校准预测概率
- 3.4、半朴素贝叶斯
- 3.5、贝叶斯网
-
- 3.5.1、概念与组成
- 3.5.2、结构
- 3.5.3、学习
- 3.5.4、推断
- 3.6、贝叶斯网络的应用
-
- 3.6.1、中文分词
- 3.6.2、机器翻译
- 3.6.3、故障诊断
- 3.6.4、疾病诊断
- 修订
- 参考
大纲总览
一、贝叶斯相关概念
可以说,机器学习的模型是来源于统计学知识,而最具统计学代表性的算法便是朴素贝叶斯分类算法。这套算法的基石便是贝叶斯定理,这套定理不仅仅名扬于机器学习,更渗透进A.I.的方方面面,比如:语音技术的处理(针对人类语言的多义性),本质上是找到概率最大的文字序列。
1.1、频率学派和贝叶斯学派
在概率学中有两大学派,频率学派(Frequentist)和贝叶斯学派(Bayesian)。它们对“概率”有不同的理解,“概率”本身表示事情发生的可能性,前者认为这种“可能性”是客观存在与这个世界的,而后者认为是存在于我们的主观想法里的。
两种学派都有自己的道理,都很难说服对方,但机器学习更偏向于贝叶斯学派。
1.1.1、频率学派
(1)特点
频率学派偏向于客观性,从自然的角度出发,试图为事件本身建模。
频率学派只相信客观能测量的东西,认为概率是频率在无限次重复实验时的极限值。
例如:
抛硬币,抛 N N N 次( N N N 是一个大数),记录下来正面向上的次数为 n n n,因此,硬币正面向上的概率为 n / N n/N n/N。
(2)定义
古典概型对概率的定义:实验 A A A 在独立重复实验中,发生的频率趋于极限 p p p,该常数 p p p 为事件 A A A 发生的概率,记为 P ( A ) = p P(A)=p P(A)=p
包含两个核心点:
- 事件 A A A 发生的概率是重复多次进行同一实验得到的
- 事件 A A A 发生的概率是常数
(3)局限性
对评估不可重复实验事件发生的概率有很大的局限性。如:陨石撞击地球、地震等等。
1.1.2、贝叶斯学派
(1)特点
贝叶斯学派偏向于主观性,认为概率只不过是我们我们思想中对事情发生的可能性的一种猜测,从观察者的角度出发,根据自己的经验,使用自己的一套方法做出推断,因为观察者自身知识能力有限,推断的结果不一定正确,但随着自身对事物认知的提高,不断修正自己的认知,那套方法也有所改变和提升。
例如:
通过观察者自己的认知,认为硬币是均匀的,正面朝上和反面朝上的概率应该各占一半,所以研究的样本特征为硬币均匀,正面朝上的概率为50%,这就是先验概率。然而经过一些实验发现,正面朝上只有20%,观察者开始怀疑硬币并不是均匀的,或者有空气流动干扰等等,因为没有完整的信息作为论证,只能采用似真推断(plausible reasoning),对各种可能的结果赋予一个合理性(plausibility),于是原来的样本特征“硬币均匀”更新为“硬币不均匀”、“空气流动”等等新特征,于是,通过观察者知识状态在新的观测后不断发生更新,最后得出正面朝上的概率结果也不断地变化。
在先验概率的基础上,结合各种不同的实验结果(似然度或条件概率)去修正先验概率,这样得出来的结果便是后验概率。
(2)定义
贝叶斯学派对概率的定义:事件 A A A 发生的概率是当前数据集 D D D 下的概率,即条件概率 P ( A ∣ D ) P(A|D) P(A∣D);当观测数据集更新为 D 1 D_1 D1时,则事件 A A A 发生的概率为P(A|D1),不同的数据集预测事件A发生的概率不同。
贝叶斯学派评估事件A发生的概率会引用先验概率和后验概率两个概念来得出结果。
包含三个核心点:
- 事件 A A A 发生的概率是变化的,并非常数
- 事件 A A A 发生的概率是特定数据集下的条件概率
- 事件 A A A 发生的概率是后验概率,且事件 A A A 发生的先验概率已给定
后验比例 = 先验比例 x 可能性比例
(3)局限性
设定合理反映事件 A A A 发生的先验概率比较难,不同先验概率所获得的结果不同。
1.2、概率论基础知识
(1)先验概率
先验概率(prior probability),根据以往的经验和分析得到的概率。
比如:抛一枚硬币正面朝上的概率为50%
(2)条件概率
设 A 、 B A、B A、B是两个事件,且 p ( A ) > 0 p(A)>0 p(A)>0,称
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
为在事件 A A A 发生的条件下事件 B B B 发生的概率。 P ( B ∣ A ) P(B|A) P(B∣A)为条件概率, P ( A ) P(A) P(A) 和 P ( B ) P(B) P(B) 是先验概率。
P ( A B ) P(AB) P(AB) 为 A A A 和 B B B 同时发生的概率,即联合概率,还可以表示为 P ( A , B ) P(A, B) P(A,B)
(3)乘法定理
设 A 、 B A、B A、B是两个事件,且 p ( A ) > 0 p(A)>0 p(A)>0,若 A A A 和 B B B 相关,求同时发生的概率
P ( A B ) = P ( A ) P ( B ∣ A ) P(AB) = P(A)P(B|A) P(AB)=P(A)P(B∣A)
A B AB AB 同时发生的概率 = A A A发生的概率 x 在 A A A发生的条件下 B B B发生的概率
或者
P ( A B ) = P ( B ) P ( A ∣ B ) P(AB) = P(B)P(A|B) P(AB)=P(B)P(A∣B)
A B AB AB 同时发生的概率 = B B B发生的概率 x 在 B B B发生的条件下 A A A发生的概率
若 A A A 和 B B B 不相关,则:
P ( A B ) = P ( A ) P ( B ) P(AB) = P(A)P(B) P(AB)=P(A)P(B)
(4)全概率公式:
事件 A A A 和 B B B 相关,事件 B B B 发生的所有可能结果 B 1 , B 2... , B n B1,B2 ...,Bn B1,B2...,Bn 相互独立,求事件 A A A 发生的概率为:
P ( A ) = P ( A ∣ B 1 ) P ( B 1 ) + P ( A ∣ B 2 ) P ( B 2 ) + . . . + P ( A ∣ B n ) P ( B n ) = ∑ i = 1 n P ( A ∣ B i ) P ( B i ) \begin{aligned}P(A)&=P(A|B_1)P(B_1) +P(A|B_2)P(B_2) + ... + P(A|B_n)P(B_n) \\&=\displaystyle\sum_{i=1}^n{P(A|B_i)P(B_i)}\end{aligned} P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...+P(A∣Bn)P(Bn)=i=1∑nP(A∣Bi)P(Bi)
(5)后验概率
后验概率为一种条件概率,但是限定了目标事件为隐变量取值,而其中的条件为观测结果。一般的条件概率,条件和事件都可以是任意的。
公式与条件概率类似,比如:某天开车出门时,已经堵车了,求前方发生了交通事故的概率:
P ( 交 通 事 故 ∣ 堵 车 ) = P ( 交 通 事 故 ) P ( 堵 车 ∣ 交 通 事 故 ) P ( 堵 车 ) P(交通事故|堵车) = \frac{P(交通事故)P(堵车|交通事故)}{P(堵车)} P(交通事故∣堵车)=P(堵车)P(交通事故)P(堵车∣交通事故)
1.3、贝叶斯定理
贝叶斯定理(原理):
P ( A , B ) = P ( B , A ) P(A, B) = P(B, A) P(A,B)=P(B,A)
⇒ P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) \Rightarrow P(A|B)P(B)=P(B|A)P(A) ⇒P(A∣B)P(B)=P(B∣A)P(A)
⇒ P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) \Rightarrow P(A | B) = \frac{P(A)P(B | A)}{P(B)} ⇒P(A∣B)=P(B)P(A)P(B∣A)
- P ( A ∣ B ) P(A|B) P(A∣B) 在事件B发生的条件下,A发生的概率。表示后验概率。
- P ( B ∣ A ) P(B|A) P(B∣A) 在事件A发生的条件下,B发生的概率。表示条件概率。
- P ( A ) P(A) P(A) 为事件A发生的概率。表示先验概率。
推广到机器学习的分类问题中:
假设某样本中的特征向量 x \pmb x xxx 与样本所属类型 y y y 具有因果关系。则利用贝叶斯公式,分类器要做的是:在已知样本的特征向量为 x \pmb x xxx的条件下反推样本所属的类别:
P ( y ∣ x ) = P ( x ∣ y ) P ( y ) P ( x ) \begin{aligned} P(y|\pmb x)=\frac{P(\pmb x|y)P(y)}{P(\pmb x)} \end{aligned} P(y∣xxx)=P(xxx)P(xxx∣y)P(y)
需要知道:
- 特征向量 x x x的概率分布 P ( x ) P(\pmb x) P(xxx)
- 每一类出现的概率 P ( y ) P(y) P(y),即先验概率
- 每一类样本的条件概率 P ( x ∣ y ) P(\pmb x|y) P(xxx∣y),也称似然(likelihood)
就可以计算出样本属于每一类的概率 P ( y ∣ x ) P(y|\pmb x) P(y∣xxx),即后验概率。
分类问题只需要预测类别,比较样本属于每一类的概率大小,找出该值最大的那一类即可,因此可以忽略 P ( x ) P(\pmb x) P(xxx),因为它对所有类都是相同的,简化后分类器的判别函数为:
a r g max y P ( x ∣ y ) P ( y ) \begin{aligned} arg \max_{y} P(\pmb x|y) P(y) \end{aligned} argymaxP(xxx∣y)P(y)
意思是 P ( x ∣ y ) P ( y ) P(\pmb x|y) P(y) P(xxx∣y)P(y)达到最大值时, y y y的值为多少,属于哪一个分类。
二、概率的分布
概率分布可被分为离散概率分布和连续概率分布,分别有很多种不同情况。
2.1、离散概率分布
离散概率分布分为4种类型:
- 伯努利分布
- 分类分布
- 二项分布
- 多项分布
这四种分布之间的区别可以简单记为:
| 类型 | 区别 |
|---|---|
| 伯努利分布 | 抛一次硬币 |
| 分类分布 | 抛一次色子 |
| 二项分布 | 抛多次硬币 |
| 多项分布 | 抛多次色子 |
其中最基本的是伯努利分布,由此引出伯努利实验(Bernoulli Trial)。它是只有两种可能实验结果的单次随机实验,其重点是“结果只有两种”,而且“只能实验一次”。
2.1.1、伯努利分布(Bernoulli Distribution)
又名两点分布或0-1分布。
若伯努利实验成功,则伯努利随机变量为1,否则为0。其中,成功概率为 p p p,则失败概率为 q = 1 − p q=1-p q=1−p, 0 < p < 1 0
典型例子:
抛一次硬币的概率分布,硬币正面向上的概率为 p p p,硬币反面向上的概率为 q q q。伯努利随机变量 X X X 取值只能为0或1,它的概率质量函数(描述离散型数据的概率分布)为:
X X X~ B e r n o u l l i ( p ) Bernoulli(p) Bernoulli(p)
f ( x ; p ) = p x q 1 − x = p I { x = 1 } q I { x = 0 } f(x;p)=p^xq^{1-x}=p^{I\{x=1\}}q^{I\{x=0\}} f(x;p)=pxq1−x=pI{x=1}qI{x=0}
2.1.2、分类分布(Categorical Distribution)
分类分布是实验结果种类大于2的伯努利分布。
典型例子:
抛色子,不同与抛硬币,色子的6个面对应6个不同的点数,每一面向上的概率分别为 p 1 , p 2 , p 3 , p 4 , p 5 , p 6 p_1,p_2,p_3,p_4,p_5,p_6 p1,p2,p3,p4,p5,p6(不一定每一面向上的概率为 1 / 6 1/6 1/6)。
分类随机变量 X X X 可以取值为:1,2,…,K,其中取k值得概率为 p k p_k pk,它的概率质量函数是:
X X X~ C a t e g o r i c a l ( p ) Categorical(p) Categorical(p)
f ( x ; p ) = p 1 I { x = 1 } p 2 I { x = 2 } . . . p k I { x = k } = ∏ k = 1 K p k I { x = k } \begin{aligned} f(x;p)=p_1^{I\{x=1\}}p_2^{I\{x=2\}}...p_{k}^{I\{x=k\}}= \prod_{k=1}^{K}p_k^{I\{x=k\}} \end{aligned} f(x;p)=p1I{x=1}p2I{x=2}...pkI{x=k}=k=1∏KpkI{x=k}
2.1.3、二项分布(Binomial Distribution)
二项分布是 n n n 个独立的伯努利实验。当 n = 1 n=1 n=1 时,二项分布就是伯努利分布。
二项随机变量 X X X描述 n n n 次伯努利实验成功了 x x x 次,因此 x x x 可以取值为0,1,…,n。它的概率质量函数是:
X X X~ B e r n o u l l i ( p , n ) Bernoulli(p,n) Bernoulli(p,n)
f ( x ; p , n ) = x ! n ! ( n − x ) ! p x ( 1 − p ) n − x f(x;p,n)=\frac{x!}{n!(n-x)!}p^x(1-p)^{n-x} f(x;p,n)=n!(n−x)!x!px(1−p)n−x
2.1.4 多项分布(Multinomial Distribution)
多项分布时 n n n 次分类实验。当 n = 1 n=1 n=1 时,多项分布为分类分布。
多项随机变量 X X X, 描述n次分类实验有 K K K 个结局,而第 k k k 个结局(概率为 p k p_k pk)出现了 n k n_k nk次。它的概率质量函数是:
X X X~ M u l t i n o m i a l ( p , n ) Multinomial(p,n) Multinomial(p,n)
f ( n 1 , n 2 , . . . , n k ∣ p , n ) = n ! n 1 ! n 2 ! . . . n k ! p 1 n 1 p 2 n 2 . . . p k n k = n ! ∏ k = 1 K p k n k n k ! \begin{aligned} f(n_1,n_2,...,n_k|p,n)=\frac{n!}{n_1!n_2!...n_k!}{p_1^{n_1}p_2^{n_2}...p_k^{n_k}}= n!\prod_{k=1}^{K}\frac{p_k^{n_k}}{n_k!} \end{aligned} f(n1,n2,...,nk∣p,n)=n1!n2!...nk!n!p1n1p2n2...pknk=n!k=1∏Knk!pknk
其中, ∑ k = 1 K n k = n \begin{aligned} \sum^K_{k=1}{n_k}=n \end{aligned} k=1∑Knk=n
2.2、连续概率分布
连续概率分布分为2种类型:
- 正态分布
- 贝塔分布
2.2.1、正态分布(Normal Distribution)
正态分布也称“常态分布”或“高斯分布”。
一维正态分布有两个参数 μ \mu μ和 σ 2 \sigma^2 σ2,一维正态随机变量 X X X 可取任何实数 x x x,它的概率密度函数为:
X X X~ N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)
f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) f(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2}) f(x∣μ,σ2)=2πσ21exp(−2σ2(x−μ)2)
n n n 维正态分布有向量参数 μ \mu μ 和矩阵参数 ϵ \epsilon ϵ, n n n 维正态随机变量 X X X 可取任何实数向量 x x x,它的概率密度函数为
X X X~ N n ( μ , ϵ ) N_n(\mu,\epsilon) Nn(μ,ϵ)
f ( x ∣ μ , ϵ ) = 1 ( 2 π ) n ∣ ϵ ∣ exp ( − 1 2 ( x − μ ) T ϵ − 1 ( x − μ ) ) f(x|\mu,\epsilon)=\frac{1}{\sqrt{(2\pi)^n|\epsilon|}}\exp(-\frac{1}{2}{(x-\mu)^T}{\epsilon^{-1}(x-\mu)}) f(x∣μ,ϵ)=(2π)n∣ϵ∣1exp(−21(x−μ)Tϵ−1(x−μ))
2.2.2、贝塔分布(Beta Distribution)
贝塔分布是描述概率的连续概率分布,它有两个形状参数 α \alpha α 和 β \beta β。贝塔随机变量 X X X 取值为 x x x,其中 0 ≤ x ≤ 1 0\leq x\leq1 0≤x≤1,它的概率密度函数为:
X X X~ B e t a ( α , β ) Beta(\alpha,\beta) Beta(α,β)
f ( x ; α , β ) = x α − 1 ( 1 − x ) β − 1 B ( α , β ) f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} f(x;α,β)=B(α,β)xα−1(1−x)β−1,
B ( α , β ) = τ ( α ) τ ( β ) τ ( α + β ) B(\alpha,\beta)=\frac{\tau(\alpha)\tau(\beta)}{\tau(\alpha+\beta)} B(α,β)=τ(α+β)τ(α)τ(β)
三、贝叶斯分类
朴素贝叶斯(Native Bayes)是贝叶斯中非常重要一个分类,其成功的一个重要条件是属性条件独立性假设,由于这种假设在绝大多数情况下显得太强,现实任务中这个假设往往难以成立,人们尝试在不过与增加模型复杂度的前提下,将独立性假设进行各种弱化,由此衍生出来很多新模型,比较经典有半朴素贝叶斯(Semi-Native Bayes)模型和贝叶斯网络(Bayesian Network)模型这两种。
3.1、贝叶斯决策理论
贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。对分类任务来说,在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
假设有 N N N种可能的类别标记,记为 y = { c 1 , c 2 , . . . , c N } y=\{c_1,c_2,...,c_N\} y={c1,c2,...,cN},则基于后验概率 P ( c i ∣ x ) P(c_i|x) P(ci∣x) 可获得样本 x x x 分类为 c i c_i ci 所产生的期望损失函数(也称条件风险)为:
R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x) R(ci∣x)=j=1∑NλijP(cj∣x)
其中, λ i j \lambda_{ij} λij 是将一个真实标记为 c j c_j cj,但被标记为 c i c_i ci 的样本所产生的的损失。
构建贝叶斯分类器的任务是寻找一个判定准则 h : x → y h:x\rightarrow y h:x→y,将总体风险最小化
R ( h ) = E x [ R ( h ( x ) ∣ x ) ] R(h)=E_x[R(h(x)|x)] R(h)=Ex[R(h(x)∣x)]
显然,对每一个样本 x x x,若 h h h 能最小化条件风险 R ( h ( x ) ∣ x ) R(h(x)|x) R(h(x)∣x),则总体风险 R ( h ) R(h) R(h)也将被最小化。这就产生了贝叶斯判定准则:为最小化总体风险,只需在每个样本上选择哪个能使条件风险 R ( c ∣ x ) R(c|x) R(c∣x) 最小的类别标记,即:
h ∗ ( x ) = arg min c ∈ y R ( c ∣ x ) h^*(x)=\argmin_{c\in y}R(c|x) h∗(x)=c∈yargminR(c∣x)
此时, h ∗ h^* h∗被称为贝叶斯最优分类器,与之对应的总体风险 R ( h ∗ ) R(h^*) R(h∗) 也被称为贝叶斯风险。 1 − R ( h ∗ ) 1-R(h^*) 1−R(h∗)反映了分类器所能达到的最好性能。
具体来说,若目标是最小化目标分类错误率,则误判损失 λ y \lambda_y λy 可写为:
λ y = { 0 , i = j 1 , 其 他 \lambda_y=\left\{ \begin{aligned} 0&, &i=j\\ 1&, &其他 \end{aligned} \right. λy={01,,i=j其他
此时的条件风险 R ( c ∣ x ) = 1 − P ( c ∣ x ) R(c|x)=1-P(c|x) R(c∣x)=1−P(c∣x),于是,最小化分类错误率的贝叶斯最优分类器为:
h ∗ ( x ) = arg max c ∈ y P ( c ∣ x ) h^*(x)=\argmax_{c\in y}P(c|x) h∗(x)=c∈yargmaxP(c∣x)
即对每一个样本 x x x,选择能使后验概率 P ( c ∣ x ) P(c|x) P(c∣x) 达到最大的类别标记。
通常情况下 P ( c ∣ x ) P(c|x) P(c∣x) 很难直接获得,根据贝叶斯定理:
P ( c ∣ x ) = P ( x , c ) P ( x ) = P ( c ) P ( x ∣ c ) P ( x ) P(c|x)=\frac{P(x,c)}{P(x)}=\frac{P(c)P(x|c)}{P(x)} P(c∣x)=P(x)P(x,c)=P(x)P(c)P(x∣c)
对上一个公式进行简化得:
h ∗ ( x ) = arg max c ∈ y P ( c ∣ x ) = arg max c ∈ y P ( c ) P ( x ∣ c ) P ( x ) = arg max c ∈ y P ( c ) P ( x ∣ c ) h^*(x)=\argmax_{c\in y}P(c|x)=\argmax_{c\in y}\frac{P(c)P(x|c)}{P(x)}=\argmax_{c\in y}P(c)P(x|c) h∗(x)=c∈yargmaxP(c∣x)=c∈yargmaxP(x)P(c)P(x∣c)=c∈yargmaxP(c)P(x∣c)
其中 P ( c ) P(c) P(c)是先验概率; P ( x ∣ c ) P(x|c) P(x∣c) 是样本 x x x 相对于类标记 c c c 的类条件概率,或称似然(likelihood);对于给定的样本 x x x, P ( x ) P(x) P(x)与类标记无关,即最大值取决于分子则可以去掉分母,所以估计 P ( c ∣ x ) P(c|x) P(c∣x) 的问题转化为如何基于训练数据来估计先验概率 P ( x ) P(x) P(x)和 P ( x ∣ c ) P(x|c) P(x∣c)。
3.2、参数估计
通过贝叶斯定理可知,后验概率=先验概率x条件概率(即,似然likelihood),那么,需要通过一定的手段方法去得到这三种不同类型的概率。
先验概率 P ( c ) P(c) P(c) 表示的是各类样本在样本空间内所占比例,根据大数定律,当样本集合包含充足的独立同分布样本时,可以通过各类样本出现的频率来对 P ( c ) P(c) P(c) 进行估计,即频率=概率。
而对于条件概率 P ( x ∣ c ) P(x|c) P(x∣c) 估计来说,涉及关于 x x x 所有属性的联合概率,如果直接根据样本出现的频率来估计则会遇到很多困难。
下面介绍两种估计法,他们的作用是:
| 方法 | 作用 |
|---|---|
| 极大似然估计 | 求条件概率(似然) |
| 极大后验估计 | 求后验概率 |
3.2.1、极大似然估计(Maximum Likelihood Estimation)
对于条件概率的估计,通常使用以下两种方法进行估计:
- 类似于先验概率,通过统计频率的方式来计算似然 P ( x ∣ c ) P(x|c) P(x∣c)。但这种方法涉及到计算各个不同属性的联合概率,当属性值很多且样本量很大时,估计会很麻烦。
- 使用极大似然法来进行估计,极大似然估计(ML估计),也称最大似然估计。极大似然法首先要假定条件概率 P ( x ∣ c ) P(x|c) P(x∣c) 服从某个分布,然后基于样本数据对概率分布的参数进行估计。但是这种方法的准确性严重依赖于假设的分布,如果假设的分布符合潜在的真实数据分布,则效果不错;否则效果会很糟糕。在现实应用中,这种假设通常需要一定的经验。
对于极大似然估计,记类别 c c c的条件概率为 P ( x ∣ c ) P(x|c) P(x∣c),假设对于训练集中的 N N N 个样本 X ~ = ( x 1 + x 2 + . . . + x N ) T \widetilde X=(x_1+x_2+...+x_N)^T X =(x1+x2+...+xN)T 可以被参数向量 θ \theta θ 唯一确定,那么利用训练集来估计参数,并将 P ( x i ∣ c ) P(x_i|c) P(xi∣c) 记为 P ( x i ∣ c ; θ ) P(x_i|c; \theta) P(xi∣c;θ)。因此对于参数 θ \theta θ 进行极大似然估计,就是在 θ \theta θ 的取值范围内寻找一组合适的参数使得 P ( x ∣ c ) P(x|c) P(x∣c) 最大,也就是寻找一组能够使得数据 ( x , c ) (x,c) (x,c) 出现的可能性最大的值,即:
θ ^ = arg max θ P ( X ~ ∣ θ ) = arg max θ ∑ i = 1 N P ( x i ∣ θ ; c ) \widehat{\theta}=\argmax_{\theta}P(\widetilde{X}|\theta)=\argmax_{\theta}\sum^N_{i=1}P(x_i|\theta;c) θ =θargmaxP(X ∣θ)=θargmaxi=1∑NP(xi∣θ;c)
由于直接求极大值虽然可行,但是不太方便,所以通常的做法是将似然函数取对数之后再进行极大值的求解,即:
θ ^ = arg max θ ∑ i = 1 N log P ( x i ∣ θ ; c ) \widehat{\theta}=\argmax_{\theta}\sum^N_{i=1}\log P(x_i|\theta;c) θ =θargmaxi=1∑NlogP(xi∣θ;c)
应用实例:
有一个箱子有黑球和白球,数量和比例不知。已知抽一百次,有70次是黑球,30次是白球,估计箱子中球的颜色比例?
根据题目知道是二项分布,则:假设抽中黑球的概率为 θ \theta θ,每次抽的颜色结果为 X ~ = { x 1 , x 2 , . . . x N } \widetilde{X}=\{x_1,x_2,...x_N\} X ={x1,x2,...xN}, c c c表示70次黑球和30次白球的类别事件,于是,在该模型下的抽取结果,可得似然函数:
P ( X ~ ∣ c ) = P ( x 1 ∣ c ) P ( x 2 ∣ c ) . . . P ( x N ∣ c ) = θ 70 ( 1 − θ ) 30 \begin{aligned} P(\widetilde{X}|c)&=P(x_1|c)P(x_2|c)...P(x_N|c) \\ &=\theta^{70}(1-\theta)^{30} \end{aligned} P(X ∣c)=P(x1∣c)P(x2∣c)...P(xN∣c)=θ70(1−θ)30
根据上面的公式,取对数,求极大值得:
log P ( X ~ ∣ c ) = 70 log θ × 30 log ( 1 − θ ) ∂ log P ( X ~ ∣ c ) ∂ θ = 70 θ − 30 1 − θ \begin{aligned} \log P(\widetilde{X}|c)&=70\log{\theta} \times{30\log{(1-\theta)}}\\ \frac{\partial\log{P(\widetilde{X}|c)}}{\partial{\theta}}&=\frac{70}{\theta}-\frac{30}{1-\theta} \end{aligned} logP(X ∣c)∂θ∂logP(X ∣c)=70logθ×30log(1−θ)=θ70−1−θ30
因为:
∂ log P ( X ~ ∣ c ) ∂ θ = 0 \begin{aligned} \frac{\partial\log{P(\widetilde{X}|c)}}{\partial{\theta}}&=0 \end{aligned} ∂θ∂logP(X ∣c)=0
则:
70 θ − 30 1 − θ = 0 \begin{aligned} \frac{70}{\theta}-\frac{30}{1-\theta}=0 \end{aligned} θ70−1−θ30=0
所以:
θ = 70 % \begin{aligned} \theta=70\% \end{aligned} θ=70%
即取出黑球的概率为70%,取出白球的概率为30%
极大似然估计视待估计参数为一个未知但固定的量,不考虑观察者的影响,即不考虑先验知识的影响,是传统的频率学派做法。
3.2.2、极大后验估计(Maximum A Posteriori Estimation)
极大后验估计更贴合贝叶斯学派思想的做法,也有不少人称其为“贝叶斯估计”。
后验概率 P ( c ∣ X ~ ) P(c|\widetilde X) P(c∣X ),可以理解为参数 θ \theta θ 在训练集 X ~ \widetilde X X 下所谓“真实出现的概率”,能够利用参数的先验概率 P ( θ ) P(\theta) P(θ)、样本的先验概率 P ( X ~ ) P(\widetilde{X}) P(X ) 和条件概率 P ( X ~ ∣ c ) = ∏ i = 1 N P ( x i ∣ θ ) P(\widetilde{X}|c)=\prod_{i=1}^NP(x_i|\theta) P(X ∣c)=i=1∏NP(xi∣θ)通过贝叶斯导出。
MAP估计的核心思想,就是将待估参数 θ \theta θ 看成随机变量,从而引入了极大似然估计里没有引入的、参数 θ \theta θ 的先验分布。MAP估计 θ ^ M A P \widehat{\theta}_{MAP} θ MAP 的定义为:
θ ^ M A P = arg max θ P ( θ ∣ X ~ ) = arg max θ P ( θ ) ∏ i = 0 N P ( x i ∣ θ ) \widehat{\theta}_{MAP}=\argmax_\theta P(\theta|\widetilde X)=\argmax_\theta P(\theta) \prod_{i=0}^{N}P(x_i|\theta) θ MAP=θargmaxP(θ∣X )=θargmaxP(θ)i=0∏NP(xi∣θ)
同样为了计算简捷,通常对上式取对数:
θ ^ M A P = arg max θ log P ( θ ∣ X ~ ) = arg max θ P ( θ ) [ log P ( θ ) + ∑ i = 1 N log P ( x i ∣ θ ) ] \widehat{\theta}_{MAP}=\argmax_\theta \log P(\theta|\widetilde X)=\argmax_\theta P(\theta) [\log{P(\theta)}+\sum_{i=1}^{N}\log P(x_i|\theta)] θ MAP=θargmaxlogP(θ∣X )=θargmaxP(θ)[logP(θ)+i=1∑NlogP(xi∣θ)]
从形式上看,极大后验概率估计只比极大似然估计多了 log P ( θ ) \log P(\theta) logP(θ) 这一项,不过他们背后的思想却相当不同。
然而,有意思的是,朴素贝叶斯算法在估计参数时,选了极大似然估计法,但是在做决策时则选择了MAP。
和极大似然估计相比,MAP的一个显著优势在于它可以引入所谓的“先验知识”,这正是贝叶斯学派的精髓。然而这个优势也伴随着劣势,它要求我们对模型参数有相对较好的认知,否则会相当大的影响到结果的合理性。
既然先验分布如此重要,那么是否有比较合理的、先验分布的选取方法呢?事实上,如何确定先验分布这个问题,正是贝叶斯统计中最困难、最具有争议却又必须解决的问题。虽然这个问题有很多现代的研究成果,但是遗憾的是,尚未能有一个圆满的理论和普适的方法。这里拟介绍“协调性假说”这个比较直观、容易理解的理论。
- 我们选择的参数 θ \theta θ 的先验分布,应该与由它和训练集确定的后验分布属于同一类型。
此时先验分布又叫共轭先验分布。这里面所谓的“同一类型”其实又是难有恰当定义的概念,但是可以直观的理解为:概率性质相似的所有分布归为“同一类型”。比如所有的正态分布都是“同一类型”的。
3.3、朴素贝叶斯
3.3.1、模型的计算
朴素贝叶斯分类器(native Bayes classifier)采用了“属性条件独立性假设”(attribute conditional independence assumption):对已知类别,假设所有属性相互独立,即每个属性(特征变量)独立地对分类结果(决策变量)发生影响。
基于属性条件独立假设,贝叶斯公式可以重写为:
P ( c ∣ x ) = P ( x ) P ( x ∣ c ) P ( x ) = P ( c ) P ( x ) ∏ i = 1 n P ( x i ∣ c ) \begin{aligned} P(c|x)=\frac{P(x)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod_{i=1}^nP(x_i|c) \end{aligned} P(c∣x)=P(x)P(x)P(x∣c)=P(x)P(c)i=1∏nP(xi∣c)
其中 n n n 为属性数目, x i x_i xi 为 x x x 在第 i i i 个属性上的取值,如:天气=晴。
由于对所有类别来说, P ( x ) P(x) P(x) 相同,因此贝叶斯判定准则有:
h n b ( x ) = arg max c ∈ y P ( c ) ∏ i = 1 n P ( x i ∣ c ) \begin{aligned} h_{nb}(x)=\argmax_{c\in y}P(c)\prod_{i=1}^nP(x_i|c) \end{aligned} hnb(x)=c∈yargmaxP(c)i=1∏nP(xi∣c)
这就是朴素贝叶斯分类器表达式,其训练过程是基于训练集 D D D 来估计类先验概率 : P ( c ) P(c) P(c),并为每个属性估计条件概率: P ( x i ∣ c ) P(x_i|c) P(xi∣c)。
(1)先验概率的计算
在训练集 D D D 中,第 c c c 类样本组成的集合为 D c D_c Dc,若有充足的独立同分布样本,则可以容易地估计先验概率: P ( c ) = ∣ D c ∣ ∣ D ∣ P(c)=\frac{|D_c|}{|D|} P(c)=∣D∣∣Dc∣
(2)条件概率的计算
-
对离散属性而言,令 D c , x i D_{c,x_i} Dc,xi 表示 D c D_c Dc 在第 i i i 个属性上取值为 x i x_i xi 的样本组成的集合,则条件概率 P ( x i ) ∣ c P(x_i)|c P(xi)∣c 可估计为: P ( x i ∣ c ) = ∣ D c , x i ∣ ∣ D c ∣ P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|} P(xi∣c)=∣Dc∣∣Dc,xi∣
-
对连续属性,通常先将属性特征 x i x_i xi 离散化,然后计算属于类 c c c 的训练样本落在 x i x_i xi 对应离散区间比例估计 P ( x i ∣ c ) P(x_i|c) P(xi∣c)。也可假设 P ( x i ∣ c ) P(x_i|c) P(xi∣c) 的概率分布,即似然函数(Likelihood Function),如正态分布,可考虑概率密度函数,假定 P ( c i ∣ c ) P(c_i|c) P(ci∣c)~ N ( μ c , i , σ c , i 2 ) N(\mu_{c,i}, \sigma^2_{c,i}) N(μc,i,σc,i2),其中 μ c , i \mu_{c,i} μc,i 和 σ c , i 2 \sigma_{c,i}^2 σc,i2分别是第 c c c 类样本在第 i i i 个属性上取值的均值和方差,则有: P ( c i ∣ c ) = 1 2 π σ c , i exp ( − ( x i − μ c , i ) 2 2 σ c , i 2 ) P(c_i|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,i}}\exp(-\frac{(x_i-\mu_{c,i})^2}{2\sigma^2_{c,i}}) P(ci∣c)=2πσc,i1exp(−2σc,i2(xi−μc,i)2)
-
而在 P ( x i ∣ c ) = 0 P(x_i|c)=0 P(xi∣c)=0 的时候,该概率与其他概率相乘的时候会把其他概率覆盖,因此需要引入 L a p l a c e Laplace Laplace 修正。做法是对所有类别下的划分计数都加一,从而避免了等于零的情况出现,并且在训练集较大时,修正对先验的影响也会降低到可以忽略不计。
3.3.2、模型的应用流程
朴素贝叶斯是一种有监督的分类算法,输入同样为样本特征值向量,以及对应的类标签,输出则为具有高分类功能的模型,能够根据输入的特征值预测分类结果。
| 输入 | 输出 |
|---|---|
| 向量X-样本的多种特征信息值,向量Y-对应的结果数值 | 预测模型,为线性函数。用法:输入待预测的向量X,输出预测结果向量Y |
主要分为三个阶段:
- 分类器准备阶段。这一阶段主要是对问题进行特征提取,建立问题的特征向量,并对其进行一定的划分,形成训练样本,这些工作主要由人工完成,完成质量对整个分类器的质量有着决定性的影响。
- 分类器训练阶段。根据上述分析中的公式,计算每个类别在训练样本中的出现频率,以及每个特征对每个类别的条件概率,最终获得分类器。
- 分类器应用阶段。该阶段会将待分配项输入分类器中,利用上述的公式自动进行分类。比较不同类别的后验概率,哪个概率值最大就作为预测值输出。
3.3.3、模型的特点
| 特点 | 说明 |
|---|---|
| 模型结构简单,算法易于实现 | 由于特征变量间的相互独立 |
| 算法有稳定的分类效率 | 不同特点的数据集其分类性能差别不大 |
| 数据集上的优势 | 小规模数据集上表现优秀,分类过程时空开销小 |
| 算法适合增量式训练 | 在数据量较大时,可以人为划分后,分批增量训练 |
| 运用领域 | 常用于垃圾邮件分类,以及其他文本分类,比如该新闻是属于时事、体育还是娱乐等 |
| 缺点1 | 对样本的特征维度作了“彼此独立”的假设,只有在独立性假定成立或在特征变量相关性较小的情况下才能获得近似最优的分类效果,这限制了朴素贝叶斯分类的使用 |
| 缺点2 | 需要先知道先验概率,而它很多时候不能准确知道,往往使用假设值代替,这也会导致分类误差的增大 |
3.3.4、模型的使用案例
如下西瓜数据集3.0(西瓜书P84)
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 0.774 | 0.376 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.634 | 0.264 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 0.608 | 0.318 | 是 |
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.556 | 0.215 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 0.403 | 0.237 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 0.481 | 0.149 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 0.437 | 0.211 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 0.666 | 0.091 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 0.243 | 0.267 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 0.245 | 0.057 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 0.343 | 0.099 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 0.639 | 0.161 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 0.657 | 0.198 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 0.360 | 0.370 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 0.593 | 0.042 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 0.719 | 0.103 | 否 |
使用该数据集训练一个朴素贝叶斯分类器,对下列“测1”进行分类:(西瓜书P151)
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 测1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | ? |
(1)计算类先验概率
根据最后一列属性标签来估计先验概率 P ( c ) P(c) P(c),显然有:
P ( 好 瓜 = 是 ) = 8 17 ≈ 0.471 P ( 好 瓜 = 否 ) = 9 17 ≈ 0.529 \begin{aligned} P(好瓜=是)=\frac{8}{17}\approx0.471\\ P(好瓜=否)=\frac{9}{17}\approx0.529 \end{aligned} P(好瓜=是)=178≈0.471P(好瓜=否)=179≈0.529
(2)计算条件概率
对于离散型属性:
| 属性 | 数量 |
|---|---|
| 色泽 | 3{青绿、乌黑、浅白} |
| 根蒂 | 3{蜷缩、稍蜷、硬挺} |
| 敲声 | 3{浊响、沉闷、清脆} |
| 纹理 | 3{清晰、稍糊、模糊} |
| 脐部 | 3{凹陷、稍凹、平坦} |
| 触感 | 2{硬滑、软粘} |
根据其他列属性来估计条件概率 P ( x i ∣ c ) P(x_i|c) P(xi∣c):
离散型属性(直接计算该特征值在该特征中所占比例):
P 青 绿 ∣ 是 = P ( 色 泽 = 青 绿 ∣ 好 瓜 = 是 ) = 3 8 = 0.375 P 青 绿 ∣ 否 = P ( 色 泽 = 青 绿 ∣ 好 瓜 = 否 ) = 3 9 ≈ 0.333 P 蜷 缩 ∣ 是 = P ( 根 蒂 = 蜷 缩 ∣ 好 瓜 = 是 ) = 5 8 = 0.625 P 蜷 缩 ∣ 否 = P ( 根 蒂 = 蜷 缩 ∣ 好 瓜 = 否 ) = 3 9 ≈ 0.333 P 浊 响 ∣ 是 = P ( 敲 声 = 浊 响 ∣ 好 瓜 = 是 ) = 6 8 = 0.750 P 浊 响 ∣ 否 = P ( 敲 声 = 浊 响 ∣ 好 瓜 = 否 ) = 4 9 ≈ 0.444 P 清 晰 ∣ 是 = P ( 纹 理 = 清 晰 ∣ 好 瓜 = 是 ) = 7 8 = 0.875 P 清 晰 ∣ 否 = P ( 纹 理 = 清 晰 ∣ 好 瓜 = 否 ) = 2 9 ≈ 0.222 P 凹 陷 ∣ 是 = P ( 脐 部 = 凹 陷 ∣ 好 瓜 = 是 ) = 6 8 = 0.750 P 凹 陷 ∣ 否 = P ( 脐 部 = 凹 陷 ∣ 好 瓜 = 否 ) = 2 9 ≈ 0.222 P 硬 滑 ∣ 是 = P ( 触 感 = 硬 滑 ∣ 好 瓜 = 是 ) = 6 8 = 0.750 P 硬 滑 ∣ 否 = P ( 触 感 = 硬 滑 ∣ 好 瓜 = 否 ) = 6 9 ≈ 0.667 \begin{aligned} P_{青绿|是}=P(色泽=青绿|好瓜=是)=\frac{3}{8}=0.375\\ P_{青绿|否}=P(色泽=青绿|好瓜=否)=\frac{3}{9}\approx0.333\\ P_{蜷缩|是}=P(根蒂=蜷缩|好瓜=是)=\frac{5}{8}=0.625\\ P_{蜷缩|否}=P(根蒂=蜷缩|好瓜=否)=\frac{3}{9}\approx0.333\\ P_{浊响|是}=P(敲声=浊响|好瓜=是)=\frac{6}{8}=0.750\\ P_{浊响|否}=P(敲声=浊响|好瓜=否)=\frac{4}{9}\approx0.444\\ P_{清晰|是}=P(纹理=清晰|好瓜=是)=\frac{7}{8}=0.875\\ P_{清晰|否}=P(纹理=清晰|好瓜=否)=\frac{2}{9}\approx0.222\\ P_{凹陷|是}=P(脐部=凹陷|好瓜=是)=\frac{6}{8}=0.750\\ P_{凹陷|否}=P(脐部=凹陷|好瓜=否)=\frac{2}{9}\approx0.222\\ P_{硬滑|是}=P(触感=硬滑|好瓜=是)=\frac{6}{8}=0.750\\ P_{硬滑|否}=P(触感=硬滑|好瓜=否)=\frac{6}{9}\approx0.667\\ \end{aligned} P青绿∣是=P(色泽=青绿∣好瓜=是)=83=0.375P青绿∣否=P(色泽=青绿∣好瓜=否)=93≈0.333P蜷缩∣是=P(根蒂=蜷缩∣好瓜=是)=85=0.625P蜷缩∣否=P(根蒂=蜷缩∣好瓜=否)=93≈0.333P浊响∣是=P(敲声=浊响∣好瓜=是)=86=0.750P浊响∣否=P(敲声=浊响∣好瓜=否)=94≈0.444P清晰∣是=P(纹理=清晰∣好瓜=是)=87=0.875P清晰∣否=P(纹理=清晰∣好瓜=否)=92≈0.222P凹陷∣是=P(脐部=凹陷∣好瓜=是)=86=0.750P凹陷∣否=P(脐部=凹陷∣好瓜=否)=92≈0.222P硬滑∣是=P(触感=硬滑∣好瓜=是)=86=0.750P硬滑∣否=P(触感=硬滑∣好瓜=否)=96≈0.667
连续型属性:
(1)密度|是:
均值:
μ c , i = 0.697 + 0.774 + 0.634 + 0.608 + 0.556 + 0.403 + 0.481 + 0.437 8 = 0.57375 ≈ 0.574 \mu_{c,i}=\frac{0.697+0.774+0.634+0.608+0.556+0.403+0.481+0.437}{8}=0.57375\approx0.574 μc,i=80.697+0.774+0.634+0.608+0.556+0.403+0.481+0.437=0.57375≈0.574
方差:
σ c , i 2 = ( 0.697 − 0.574 ) 2 + ( 0.774 − 0.574 ) 2 + ( 0.634 − 0.574 ) 2 + ( 0.608 − 0.574 ) 2 + ( 0.556 − 0.574 ) 2 + ( 0.403 − 0.574 ) 2 + ( 0.481 − 0.574 ) 2 + ( 0.437 − 0.574 ) 2 8 = 0.015129 + 0.04 + 0.0036 + 0.001156 + 0.000324 + 0.029241 + 0.008649 + 0.018769 8 = 0.116868 8 = 0.0146085 ≈ 0.12 1 2 \sigma^2_{c,i}=\frac{(0.697-0.574)^2+(0.774-0.574)^2+(0.634-0.574)^2+(0.608-0.574)^2+(0.556-0.574)^2+(0.403-0.574)^2+(0.481-0.574)^2+(0.437-0.574)^2}{8}=\frac{0.015129+0.04+0.0036+0.001156+0.000324+0.029241+0.008649+0.018769}{8}=\frac{0.116868}{8}=0.0146085\approx0.121^2 σc,i2=8(0.697−0.574)2+(0.774−0.574)2+(0.634−0.574)2+(0.608−0.574)2+(0.556−0.574)2+(0.403−0.574)2+(0.481−0.574)2+(0.437−0.574)2=80.015129+0.04+0.0036+0.001156+0.000324+0.029241+0.008649+0.018769=80.116868=0.0146085≈0.1212
则 σ = 0.121 \sigma=0.121 σ=0.121
P 密 度 : 0.697 ∣ 是 = P ( 密 度 = 0.697 ∣ 好 瓜 = 是 ) = 1 2 π × 0.121 exp ( − ( 0.697 − 0.574 ) 2 2 × 0.12 1 2 ) ≈ 1.967 \begin{aligned} P_{密度:0.697|是}=P(密度=0.697|好瓜=是)=\frac{1}{\sqrt{2\pi}\times{0.121}}\exp(-\frac{(0.697-0.574)^2}{2\times{0.121^2}})\approx1.967 \end{aligned} P密度:0.697∣是=P(密度=0.697∣好瓜=是)=2π×0.1211exp(−2×0.1212(0.697−0.574)2)≈1.967
(2)密度|否
均值:
μ c , i = 0.666 + 0.243 + 0.245 + 0.343 + 0.639 + 0.657 + 0.360 + 0.593 + 0.719 9 = 0.4961111111 ≈ 0.496 \mu_{c,i}=\frac{0.666+0.243+0.245+0.343+0.639+0.657+0.360+0.593+0.719}{9}=0.4961111111\approx0.496 μc,i=90.666+0.243+0.245+0.343+0.639+0.657+0.360+0.593+0.719=0.4961111111≈0.496
方差:
σ c , i 2 = ( 0.666 − 0.496 ) 2 + ( 0.243 − 0.496 ) 2 + ( 0.245 − 0.496 ) 2 + ( 0.343 − 0.496 ) 2 + ( 0.639 − 0.496 ) 2 + ( 0.657 − 0.496 ) 2 + ( 0.360 − 0.496 ) 2 + ( 0.593 − 0.496 ) 2 + ( 0.719 − 0.496 ) 2 9 = 0.0289 + 0.064009 + 0.063001 + 0.023409 + 0.020449 + 0.025921 + 0.018496 + 0.009409 + 0.049729 9 = 0.303323 9 ≈ 0.034 = 0.18 4 2 \sigma^2_{c,i}=\frac{(0.666-0.496)^2+(0.243-0.496)^2+(0.245-0.496)^2+(0.343-0.496)^2+(0.639-0.496)^2+(0.657-0.496)^2+(0.360-0.496)^2+(0.593-0.496)^2+(0.719-0.496)^2}{9}=\frac{0.0289+0.064009+0.063001+0.023409+0.020449+0.025921+0.018496+0.009409+0.049729}{9}=\frac{0.303323}{9}\approx0.034=0.184^2 σc,i2=9(0.666−0.496)2+(0.243−0.496)2+(0.245−0.496)2+(0.343−0.496)2+(0.639−0.496)2+(0.657−0.496)2+(0.360−0.496)2+(0.593−0.496)2+(0.719−0.496)2=90.0289+0.064009+0.063001+0.023409+0.020449+0.025921+0.018496+0.009409+0.049729=90.303323≈0.034=0.1842
则 σ = 0.184 \sigma=0.184 σ=0.184
P 密 度 : 0.697 ∣ 否 = P ( 密 度 = 0.697 ∣ 好 瓜 = 否 ) = 1 2 π × 0.184 exp ( − ( 0.697 − 0.496 ) 2 2 × 0.18 4 2 ) ≈ 1.193 \begin{aligned} P_{密度:0.697|否}=P(密度=0.697|好瓜=否)=\frac{1}{\sqrt{2\pi}\times{0.184}}\exp(-\frac{(0.697-0.496)^2}{2\times{0.184^2}})\approx1.193 \end{aligned} P密度:0.697∣否=P(密度=0.697∣好瓜=否)=2π×0.1841exp(−2×0.1842(0.697−0.496)2)≈1.193
(3)含糖率|是
均值:
μ c , i = 0.460 + 0.376 + 0.264 + 0.318 + 0.215 + 0.237 + 0.149 + 0.211 8 = 2.23 8 = 0.27875 ≈ 0.279 \mu_{c,i}=\frac{0.460+0.376+0.264+0.318+0.215+0.237+0.149+0.211}{8}=\frac{2.23}{8}=0.27875\approx0.279 μc,i=80.460+0.376+0.264+0.318+0.215+0.237+0.149+0.211=82.23=0.27875≈0.279
方差:
σ c , i 2 = ( 0.460 − 0.279 ) 2 + ( 0.376 − 0.279 ) 2 + ( 0.264 − 0.279 ) 2 + ( 0.318 − 0.279 ) 2 + ( 0.215 − 0.279 ) 2 + ( 0.237 − 0.279 ) 2 + ( 0.149 − 0.279 ) 2 + ( 0.211 − 0.279 ) 2 8 = 0.032761 + 0.009409 + 0.000225 + 0.001521 + 0.004096 + 0.001764 + 0.0169 + 0.004624 8 = 0.0713 8 = 0.0089125 ≈ 0.09 4 2 \sigma^2_{c,i}=\frac{(0.460-0.279)^2+(0.376-0.279)^2+(0.264-0.279)^2+(0.318-0.279)^2+(0.215-0.279)^2+(0.237-0.279)^2+(0.149-0.279)^2+(0.211-0.279)^2}{8}=\frac{0.032761+0.009409+0.000225+0.001521+0.004096+0.001764+0.0169+0.004624}{8}=\frac{0.0713}{8}=0.0089125\approx0.094^2 σc,i2=8(0.460−0.279)2+(0.376−0.279)2+(0.264−0.279)2+(0.318−0.279)2+(0.215−0.279)2+(0.237−0.279)2+(0.149−0.279)2+(0.211−0.279)2=80.032761+0.009409+0.000225+0.001521+0.004096+0.001764+0.0169+0.004624=80.0713=0.0089125≈0.0942
则 σ = 0.094 \sigma=0.094 σ=0.094
P 含 糖 : 0.460 ∣ 是 = P ( 密 度 = 0.460 ∣ 好 瓜 = 是 ) = 1 2 π × 0.094 exp ( − ( 0.460 − 0.279 ) 2 2 × 0.09 4 2 ) ≈ 0.665 \begin{aligned} P_{含糖:0.460|是}=P(密度=0.460|好瓜=是)=\frac{1}{\sqrt{2\pi}\times{0.094}}\exp(-\frac{(0.460-0.279)^2}{2\times{0.094^2}})\approx0.665 \end{aligned} P含糖:0.460∣是=P(密度=0.460∣好瓜=是)=2π×0.0941exp(−2×0.0942(0.460−0.279)2)≈0.665
(4)含糖率|否
均值:
μ c , i = 0.091 + 0.267 + 0.057 + 0.099 + 0.161 + 0.198 + 0.370 + 0.042 + 0.103 9 = 1.388 9 = 0.1542222 ≈ 0.154 \mu_{c,i}=\frac{0.091+0.267+0.057+0.099+0.161+0.198+0.370+0.042+0.103}{9}=\frac{1.388}{9}=0.1542222\approx0.154 μc,i=90.091+0.267+0.057+0.099+0.161+0.198+0.370+0.042+0.103=91.388=0.1542222≈0.154
方差:
σ c , i 2 = ( 0.091 − 0.154 ) 2 + ( 0.267 − 0.154 ) 2 + ( 0.057 − 0.154 ) 2 + ( 0.099 − 0.154 ) 2 + ( 0.161 − 0.154 ) 2 + ( 0.198 − 0.154 ) 2 + ( 0.370 − 0.154 ) 2 + ( 0.042 − 0.154 ) 2 + ( 0.103 − 0.154 ) 2 9 = 0.003969 + 0.012769 + 0.009409 + 0.003025 + 0.000049 + 0.001936 + 0.046656 + 0.012544 + 0.002601 9 = 0.092958 9 ≈ 0.10 2 2 \sigma^2_{c,i}=\frac{(0.091-0.154)^2+(0.267-0.154)^2+(0.057-0.154)^2+(0.099-0.154)^2+(0.161-0.154)^2+(0.198-0.154)^2+(0.370-0.154)^2+(0.042-0.154)^2+(0.103-0.154)^2}{9}=\frac{0.003969+0.012769+0.009409+0.003025+0.000049+0.001936+0.046656+0.012544+0.002601}{9}=\frac{0.092958}{9}\approx0.102^2 σc,i2=9(0.091−0.154)2+(0.267−0.154)2+(0.057−0.154)2+(0.099−0.154)2+(0.161−0.154)2+(0.198−0.154)2+(0.370−0.154)2+(0.042−0.154)2+(0.103−0.154)2=90.003969+0.012769+0.009409+0.003025+0.000049+0.001936+0.046656+0.012544+0.002601=90.092958≈0.1022
则 σ = 0.102 \sigma=0.102 σ=0.102
P 含 糖 : 0.460 ∣ 否 = P ( 含 糖 = 0.460 ∣ 好 瓜 = 否 ) = 1 2 π × 0.102 exp ( − ( 0.460 − 0.154 ) 2 2 × 0.10 2 2 ) ≈ 0.043 \begin{aligned} P_{含糖:0.460|否}=P(含糖=0.460|好瓜=否)=\frac{1}{\sqrt{2\pi}\times{0.102}}\exp(-\frac{(0.460-0.154)^2}{2\times{0.102^2}})\approx0.043 \end{aligned} P含糖:0.460∣否=P(含糖=0.460∣好瓜=否)=2π×0.1021exp(−2×0.1022(0.460−0.154)2)≈0.043
于是有:
P ( 好 瓜 = 是 ) × P ( 青 绿 ∣ 是 ) × P ( 蜷 缩 ∣ 是 ) × P ( 浊 响 ∣ 是 ) × P ( 清 晰 ∣ 是 ) × P ( 凹 陷 ∣ 是 ) × P ( 硬 滑 ∣ 是 ) × P ( 密 度 : 0.697 ∣ 是 ) × P ( 含 糖 : 0.460 ∣ 是 ) = 0.471 × 0.375 × 0.625 × 0.750 × 0.875 × 0.750 × 0.750 × 1.967 × 0.665 ≈ 0.053 P(好瓜=是)\times P(青绿|是)\times P(蜷缩|是)\times P(浊响|是) \times P(清晰|是)\times P(凹陷|是)\times P(硬滑|是)\times P(密度:0.697|是)\times P(含糖:0.460|是)=0.471\times0.375\times0.625\times 0.750\times 0.875\times 0.750\times 0.750\times 1.967\times 0.665 \approx0.053 P(好瓜=是)×P(青绿∣是)×P(蜷缩∣是)×P(浊响∣是)×P(清晰∣是)×P(凹陷∣是)×P(硬滑∣是)×P(密度:0.697∣是)×P(含糖:0.460∣是)=0.471×0.375×0.625×0.750×0.875×0.750×0.750×1.967×0.665≈0.053
P ( 好 瓜 = 否 ) × P ( 青 绿 ∣ 否 ) × P ( 蜷 缩 ∣ 否 ) × P ( 浊 响 ∣ 否 ) × P ( 清 晰 ∣ 否 ) × P ( 凹 陷 ∣ 否 ) × P ( 硬 滑 ∣ 否 ) × P ( 密 度 : 0.697 ∣ 否 ) × P ( 含 糖 : 0.460 ∣ 否 ) = 0.529 × 0.333 × 0.333 × 0.444 × 0.222 × 0.222 × 0.667 × 1.193 × 0.043 ≈ 4.39 × 1 0 − 5 P(好瓜=否)\times P(青绿|否)\times P(蜷缩|否)\times P(浊响|否) \times P(清晰|否)\times P(凹陷|否)\times P(硬滑|否)\times P(密度:0.697|否)\times P(含糖:0.460|否)=0.529\times 0.333\times0.333\times0.444\times 0.222\times 0.222\times 0.667\times 1.193\times 0.043\approx4.39\times 10^{-5} P(好瓜=否)×P(青绿∣否)×P(蜷缩∣否)×P(浊响∣否)×P(清晰∣否)×P(凹陷∣否)×P(硬滑∣否)×P(密度:0.697∣否)×P(含糖:0.460∣否)=0.529×0.333×0.333×0.444×0.222×0.222×0.667×1.193×0.043≈4.39×10−5
由于 0.053 > 4.39 × 1 0 − 5 0.053\gt 4.39\times 10^{-5} 0.053>4.39×10−5,因此朴素贝叶斯分类器将测试样本“测1”判别为“好瓜”。
Laplace拉普拉斯修正
若测试集某一个属性值在训练集中没有与之对应的类,如“敲声=清脆”属性,没有“好瓜=是”的分类,则会出现该属性下条件概率为0的情况:
P ( 清 脆 ∣ 是 ) = P ( 敲 声 = 清 脆 ∣ 好 瓜 = 是 ) = 0 8 = 0 P(清脆|是)=P(敲声=清脆|好瓜=是)=\frac{0}{8}=0 P(清脆∣是)=P(敲声=清脆∣好瓜=是)=80=0
随后无论是其他属性的条件概率值为多少,由于连乘其结果都会为0,即最小(概率无负数),会被分为“好瓜=否”,这样显然不太合理。
为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”,在估计概率值时,通常要进行“平滑”(smoothing),常用“拉普拉斯修正”(Laplacian correction)。具体来说,令 N N N 表示训练集 D D D 中可能的类别数, N i N_i Ni 表示第 i i i 个属性可能的取值,则前面先验概率和条件概率可以被修正为:
P ^ ( c ) = ∣ D c ∣ + 1 ∣ D ∣ + N \widehat P(c)=\frac{|D_c|+1}{|D|+N} P (c)=∣D∣+N∣Dc∣+1
P ^ ( x i ∣ c ) = ∣ D c i x i ∣ + 1 ∣ D c ∣ + N i \widehat P(x_i|c)=\frac{|D_{c_ix_i}|+1}{|D_{c}|+N_i} P (xi∣c)=∣Dc∣+Ni∣Dcixi∣+1
于是本例子中,先验概率可估计为:
P ^ ( 好 瓜 = 是 ) = 8 + 1 17 + 2 ≈ 0.474 \widehat P(好瓜=是)=\frac{8+1}{17+2}\approx0.474 P (好瓜=是)=17+28+1≈0.474
P ^ ( 好 瓜 = 否 ) = 9 + 1 17 + 2 ≈ 0.526 \widehat P(好瓜=否)=\frac{9+1}{17+2}\approx0.526 P (好瓜=否)=17+29+1≈0.526
类似的,条件概率可估计为:
P ^ 青 绿 ∣ 是 = P ^ ( 色 泽 = 青 绿 ∣ 好 瓜 = 是 ) = 3 + 1 8 + 3 ≈ 0.364 \widehat P_{青绿|是}=\widehat P(色泽=青绿|好瓜=是)=\frac{3+1}{8+3}\approx 0.364 P 青绿∣是=P (色泽=青绿∣好瓜=是)=8+33+1≈0.364
P ^ 青 绿 ∣ 否 = P ^ ( 色 泽 = 青 绿 ∣ 好 瓜 = 否 ) = 3 + 1 9 + 3 ≈ 0.333 \widehat P_{青绿|否}=\widehat P(色泽=青绿|好瓜=否)=\frac{3+1}{9+3}\approx 0.333 P 青绿∣否=P (色泽=青绿∣好瓜=否)=9+33+1≈0.333
其余的类似,并且上面提到的概率 P 清 脆 ∣ 是 P_{清脆|是} P清脆∣是 可估计为:
P ^ 清 脆 ∣ 是 = P ^ ( 敲 声 = 清 脆 ∣ 好 瓜 = 是 ) = 0 + 1 8 + 3 ≈ 0.091 \widehat P_{清脆|是}=\widehat P(敲声=清脆|好瓜=是)=\frac{0+1}{8+3}\approx 0.091 P 清脆∣是=P (敲声=清脆∣好瓜=是)=8+30+1≈0.091
拉普拉斯修正实质上假设了属性值与类别均匀分布,这是在朴素贝叶斯学过程中额外引入的的关于数据的先验。显然拉普拉斯修正避免了因训练样本不充分而导致概率估计值为0的问题,并且在训练值变大时,修正过程所引入的先验(prior)的影响也会逐渐变得可忽略,使得估值趋向于实际概率值。
在现实任务中,朴素贝叶斯分类器有多种使用方法。例如:
- 若任务对预测速度要求较高,则对给定训练集,可将朴素贝叶斯分类器设计的所有概率估值事先计算好存储起来,这样在进行预测时只需“查表”即可进行判别。
- 若任务数据更替频繁,则可采用“懒惰学习”(lazy learning)(如KNN为代表)方式,先不进行任何训练,待收到预测请求时,再根据当前数据集进行概率估值。
- 若数据不断增加,则可在现有估值基础上,仅对新增样本的属性值所涉及的概率估值进行计数修正即可实现增量学习。
3.3.5、在Python中使用朴素贝叶斯分类算法
原理回顾:
贝叶斯分类器是基于下面的公式工作的:
P ( y ∣ x 1 , x 2 , . . . , x j ) = P ( x 1 , . . . x j ∣ y ) P ( y ) P ( x 1 , x 2 , . . . x j ) P(y|x_1,x_2,...,x_j)=\frac{P(x_1,...x_j|y)P(y)}{P(x_1,x_2,...x_j)} P(y∣x1,x2,...,xj)=P(x1,x2,...xj)P(x1,...xj∣y)P(y)
其中:
P ( y ∣ x 1 , x 2 , . . . , x j ) P(y|x_1,x_2,...,x_j) P(y∣x1,x2,...,xj) - 后验概率 。一个观察值在其 j j j 个特征是 x 1 , x 2 , . . . , x j x_1,x_2,...,x_j x1,x2,...,xj 的情况下,它的分类是类别 y y y 的概率。
P ( x 1 , x 2 , . . . , x j ∣ y ) P(x_1,x_2,...,x_j|y) P(x1,x2,...,xj∣y) - 似然概率 。给定观测值的分类 y y y,其特征是 x 1 , x 2 , . . . , x j x_1,x_2,...,x_j x1,x2,...,xj 的概率。
P ( y ) P(y) P(y) - 先验概率 。查看数居前对于分类 y y y 出现概率的猜测。
P ( x 1 , x 2 , . . . , x j ) P(x_1,x_2,...,x_j) P(x1,x2,...,xj) - 边缘概率 。 j j j 个特征同时出现的概率。
模型的介绍:
安装 scikit-learn:
python -m pip install scikit-learn
注意numpy需要1.19.3版本,否则为1.19.4新版会报错(2020年测),此时:
python -m pip install numpy==1.19.3
在Scikit-Learn中,基于贝叶斯这一大类的算法模型的相关库都在sklearn.native_bayes包之中。根据似然度计算方法不同,朴素贝叶斯分成几个具体的算法分支:
| 算法 | 运用 | 使用场景 |
|---|---|---|
| 伯努利朴素贝叶斯(BernoulliNB) | 特征变量是布尔变量,符合0/1分布,在文档分类中特征是单词否出现 |
文本分类 |
| 多项式朴素贝叶斯(MultinomialNB) | 特征变量是离散变量,符合多项分布,在文档分类中,特征变量体现在一个单词出现的次数,或者是单词的TF-IDF值等 |
文本分类,使用词袋或者TF-IDF方法 |
| 高斯贝叶斯(GaussianNB) | 特征变量是连续变量,符合高斯分布,比如人的身高,物体的长度 |
文本分类 |
多项式模型朴素贝叶斯和伯努利模型朴素贝叶斯常用在文本分类问题中,高斯分布的朴素贝叶斯主要用于连续变量中,且假设连续变量是服从正太分布的。
3.3.5.1 伯努利朴素贝叶斯
说明:
目标数据特征概率分布:多重伯努利分布,即有多个特征,但每个特征都假设是一个二元(Bernoulli, boolean)变量。
这类算法要求样本以二元值特征向量表示;如果样本含有其他类型的数据,一个BernoulliNB实例会将其二值化(取决于binarize参数)。
与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i ,而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
在文本分类的例子中,词频向量(word occurrence vectors)(而非词数向量(word count vectors))可能用于训练和用于这个分类器。 BernoulliNB 可能在一些数据集上可能表现得更好,特别是那些更短的文档。 如果时间允许,建议对伯努利和多项式两个模型都进行评估。
例子:
# 加载库
import numpy as np
from sklearn.naive_bayes import BernoulliNB
# 创建三个二元特征,100个样本
features = np.random.randint(2, size=(100, 3))
# 创建一个二元目标向量
target = np.random.randint(2, size=(100, 1)).ravel()
# 给定每个分类的先验概率,创建一个伯努利朴素贝叶斯对象
classifer = BernoulliNB(class_prior=[0.25, 0.5])
# 训练模型
model = classifer.fit(features, target)
模型与方法:
模型:
BernoulliNB(*, alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)
| 参数 | 说明 |
|---|---|
| alpha | 平滑因子,默认为1。alpha=0,不做平滑;alpha=1,Laplace平滑,避免0概率出现;0 |
| binarize | 样本特征二值化的阈值,默认是0。如果不输入,则模型会认为所有特征都已经是二值化形式了;如果输入具体的值,则模型会把大于该值的部分归为一类,小于的归为另一类。 |
| fit_prior | 是否去学习类的先验概率,默认是True |
| class_prior_prior | 列表类型。各个类别的先验概率,如果没有指定,则模型会根据数据自动学习, 每个类别的先验概率相同,等于类标记总个数N分之一。 |
方法:
| 方法 | 说明 |
|---|---|
| fit(X,Y) | 在数据集(X,Y)上拟合模型 |
| get_params() | 获取模型参数 |
| predict(X) | 对数据集X进行预测 |
| predict_log_proba(X) | 对数据集X预测,得到每个类别的概率对数值 |
| predict_proba(X) | 对数据集X预测,得到每个类别的概率 |
| score(X,Y) | 得到模型在数据集(X,Y)的得分情况 |
3.3.5.2 多项式朴素贝叶斯
说明:
MultinomialNB 实现了服从多项分布数据的朴素贝叶斯算法,也是用于文本分类(这个领域中数据往往以词向量表示,尽管在实践中 tf-idf 向量在预测时表现良好)的两大经典朴素贝叶斯算法之一。 分布参数由每类 y y y 的 θ y = ( θ y 1 , . . . , θ y n ) \theta_y=(\theta{y_1},...,\theta{y_n}) θy=(θy1,...,θyn) 向量决定,式中 n n n 是特征的数量(对于文本分类,是词汇量的大小), θ y i \theta_{y_i} θyi 是样本中属于类 y y y 中特征 i i i 概率 P ( x i ∣ y ) P(x_i|y) P(xi∣y),参数 θ \theta θ 使用平滑过的最大似然估计法来估计,即相对频率计数:
θ ^ = N y i + α N y + α n \widehat{\theta}=\frac{N_{y_i}+\alpha}{N_y+\alpha n} θ =Ny+αnNyi+α
式中 N y i = ∑ x ∈ T x i N_{y_i}=\sum_{x\in T}x_i Nyi=∑x∈Txi 表示特征 i i i 出现在 y y y 类的训练集 T T T 中, N y = ∑ i = 1 n N y i N_{y}=\sum^n_{i=1}N_{y_i} Ny=∑i=1nNyi 表示类 y y y 所有特征总量。
先验平滑因子 α ≥ 0 \alpha\geq0 α≥0 应用于在学习样本中没有出现的特征,以防在将来的计算中出现0概率输出,把 α = 1 \alpha=1 α=1 称为拉普拉斯平滑(Lapalce smoothing),而 α < 0 \alpha\lt0 α<0 被称为利德斯通平滑(Lidstone smoothing)。
例子:
创建一个玩具文本数据集,含有3个观察值(3句话),然后把文本子字符串转换为词袋特征矩阵和一个目标向量,再使用MultinomialNB来训练一个模型,并给定两个分类(支持巴西队和支持德国队)的先验概率。
# 加载库
import numpy as np
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer
# 创建文本
text_data = np.array(['I love Brazil. Brazil!', 'Brazil is best', 'Germany beats both'])
# 创建词袋
count = CountVectorizer()
bag_of_words = count.fit_transform(text_data)
# 创建特征矩阵
features = bag_of_words.toarray()
# 创建目标向量
target = np.array([0, 0, 1])
# 给定每个分类的先验概率,创建一个多项式朴素贝叶斯对象
classifer = MultinomialNB(class_prior=[0.25, 0.5])
# 训练模型
model = classifer.fit(features, target)
# 创建一个观察值
new_observation = [[0, 0, 0, 1, 0, 1, 0]]
# 预测观察值的分类
model.predict(new_observation)
# array([0])
模型与方法(同上):
模型:
MultinomialNB(*, alpha=1.0, fit_prior=True, class_prior=None)
| 参数 | 说明 |
|---|---|
| alpha | 平滑因子,默认为1。alpha=0,不做平滑;alpha=1,Laplace平滑,避免0概率出现;0 |
| binarize | 样本特征二值化的阈值,默认是0。如果不输入,则模型会认为所有特征都已经是二值化形式了;如果输入具体的值,则模型会把大于该值的部分归为一类,小于的归为另一类。 |
| fit_prior | 是否去学习类的先验概率,默认是True |
| class_prior_prior | 列表类型。各个类别的先验概率,如果没有指定,则模型会根据数据自动学习, 每个类别的先验概率相同,等于类标记总个数N分之一。 |
方法:
| 方法 | 说明 |
|---|---|
| fit(X,Y) | 在数据集(X,Y)上拟合模型 |
| get_params() | 获取模型参数 |
| predict(X) | 对数据集X进行预测 |
| predict_log_proba(X) | 对数据集X预测,得到每个类别的概率对数值 |
| predict_proba(X) | 对数据集X预测,得到每个类别的概率 |
| score(X,Y) | 得到模型在数据集(X,Y)的得分情况 |
3.3.5.3 高斯朴素贝叶斯
说明:
GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:

参数 σ y \sigma_y σy 和 μ y \mu_y μy 使用最大似然估计法。
举例:
# 加载库
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
# 加载数据
iris = datasets.load_iris()
features = iris.data
target = iris.target
# 创建高斯朴素贝叶斯对象
classifer = GaussianNB()
# 训练模型
model = classifer.fit(features, target)
# 预测模型
y_pred = model.predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d" % (features.shape[0], (target != y_pred).sum()))
# Number of mislabeled points out of a total 150 points : 6
模型和方法:
模型:
GaussianNB(*, priors=None, var_smoothing=1e-09)
| 参数 | 说明 |
|---|---|
| priors | 先验概率大小,如果没有给定,模型则根据样本数据自己计算(利用极大似然法) |
方法:
| 方法 | 说明 |
|---|---|
| fit(X,Y) | 在数据集(X,Y)上拟合模型 |
| get_params() | 获取模型参数 |
| predict(X) | 对数据集X进行预测 |
| predict_log_proba(X) | 对数据集X预测,得到每个类别的预测概率对数值 |
| predict_proba(X) | 对数据集X预测,得到每个类别的预测概率 |
| score(X,Y) | 得到模型在数据集(X,Y)的得分情况 |
注意:
GaussianNB产生的预测概率(使用predict_proba输出)是没有经过校正的,即不可信的,需要使用保序回归(isotonic regression)或者其他相关方法。
3.3.5.4 校准预测概率
使用 CalibratedClassifierCV
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.calibration import CalibratedClassifierCV
# 加载数据
iris = datasets.load_iris()
features = iris.data
target = iris.target
# 创建高朴素贝叶斯对象
classifer = GaussianNB()
# 创建使用 sigmoid 校准调校过的交叉验证模型
classifer_sigmoid = CalibratedClassifierCV(classifer, cv=2, method='sigmoid')
# 校准概率
classifer_sigmoid.fit(features, target)
# 创建新的观测值
new_observation = [[2.6, 2.6, 2.6, 0.4]]
# 查看校准过的概率
classifer_sigmoid.predict_proba(new_observation)
# array([[0.31859969, 0.63663466, 0.04476565]])
# 原始预测概率,不使用校准,得到很极端的概率预测值
classifer.fit(features, target).predict_proba(new_observation)
# array([[2.31548432e-04, 9.99768128e-01, 3.23532277e-07]])
CalibratedclassifierCV提供了两种校准方法: Platt sigmoid模型和保序回归,可以通过method参数进行设置。保序回归是无参的,在样本量很小的情况下,它往往会过拟合,比如本案例中的鸢尾花数据集,只有150个观察值。
3.4、半朴素贝叶斯
为了降低贝叶斯公式中估计后验概率 P ( c ∣ x ) P(c|x) P(c∣x) 的困难,朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立,于是人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了一类称为“半朴素贝叶斯分类器”(semi-native Bayes classifiers)的学习方法。
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
“独依赖估计”(One-Dependent Estimator,ODE)是半朴素贝叶斯分类器最常用的一种策略。顾名思义,所谓“独依赖”就是假设每个属性在类别之外最多仅依赖于一个其他属性,即:
P ( c ∣ x ) ∝ P ( c ) ∏ i = 1 d P ( x i ∣ c , p a i ) P(c|x) \propto{P(c)}\prod^d_{i=1}P(x_i|c,pa_i) P(c∣x)∝P(c)i=1∏dP(xi∣c,pai)
其中 p a i pa_i pai 为属性 x i x_i xi 所依赖的属性,称为 x i x_i xi 的父属性。对于每个属性,若父属性已知,则可以采用朴素贝叶斯计算条件概率的方法来估值计算 P ( x i ∣ c , p a i ) P(x_i|c,pa_i) P(xi∣c,pai)。于是问题的关键就是:如何确定每个属性的父属性,不同的做法产生不同的独依赖分类器,具体如下两种:
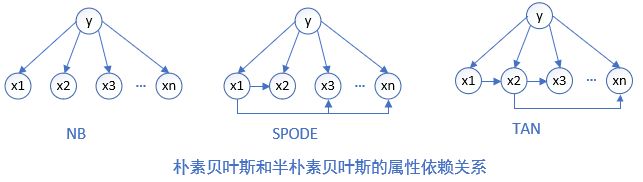
- SPODE(Super-Parent ODE)方法。最直接的方法,假设所有属性都依赖于同一个属性,称为“超父”(super parent),然后通过交叉验证等模型选择方法来确定超父属性。如上图 x 1 x_1 x1 是超父。
- TAN(Tree Augmented native Bayes)方法。在最大带权生成树(maximum weighted spanning tree)算法的基础上,通过以下步骤将属性间依赖关系约简为以上的树形结构:
- 计算任意两个属性之间的条件互信息(conditional mutual information) I ( x i , x j ∣ y ) = ∑ x i , x j ; c ∈ y P ( x i , x j ∣ c ) l o g P ( x i , x j ∣ c ) P ( x i ∣ c ) P ( x j ∣ c ) I(x_i,x_j|y)=\sum_{x_i,x_j;c\in y}P(x_i,x_j|c)log\frac{P(x_i,x_j|c)}{P(x_i|c)P(x_j|c)} I(xi,xj∣y)=∑xi,xj;c∈yP(xi,xj∣c)logP(xi∣c)P(xj∣c)P(xi,xj∣c)
- 以属性为节点构建完全图,任意两个节点之间边的权重设为 I ( x i , x j ∣ y ) I(x_i,x_j|y) I(xi,xj∣y)
- 构建此完全图的最大带权生成树,挑选根变量,将边置为有向
- 加入类别节点 y y y,增加从 y y y 到每个属性的有向边。
互信息 I ( x i , x j ∣ y ) I(x_i,x_j|y) I(xi,xj∣y) 刻画了属性 x i x_i xi 和 x j x_j xj 在已知类别情况下的相关性,因此通过最大生成树算法,TAN实际上仅保留了强相关属性之间的依赖性。
- AODE(Averaged One-Dependent Estimator) 是一种基于集成学习机制、更为强大的独依赖分类器。与SPODE通过模型选择确定超父属性不同,AODE尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果,即: P ( c ∣ x ) ∝ ∑ i = 1 ∣ D x i ∣ ≥ m ′ d P ( c , x i ) ∏ j = 1 d P ( x j ∣ c , x i ) P(c|x)\propto \sum^d_{\underset {|D_{x_i}|\geq m^{'}}{i=1}}P(c,x_i)\prod^d_{j=1}P(x_j|c,x_i) P(c∣x)∝∣Dxi∣≥m′i=1∑dP(c,xi)j=1∏dP(xj∣c,xi)其中 D x i D_{x_i} Dxi 是在第 i i i 个属性上取值为 x i x_i xi 的样本的集合, m ′ m^{'} m′为阈值常数,默认设置为30。显然AODE需估计 P ( c , x i ) P(c,x_i) P(c,xi) 和 P ( x j ∣ c , x i ) P(x_j|c,x_i) P(xj∣c,xi)。类似式,先验概率和条件概率为: P ( c , x i ) ^ = ∣ D c , x i + 1 ∣ ∣ D ∣ + N × N i \hat{P(c,x_i)}=\frac{|D_{c,x_i}+1|}{|D|+N\times N_i} P(c,xi)^=∣D∣+N×Ni∣Dc,xi+1∣ P ( x j ∣ c , x i ) ^ = ∣ D c , x i , x j ∣ + 1 ∣ D c , x i ∣ + N j \hat{P(x_j|c,x_i)}=\frac{|D_{c,x_i,x_j}|+1}{|D_{c,x_i}|+N_j} P(xj∣c,xi)^=∣Dc,xi∣+Nj∣Dc,xi,xj∣+1 其中 N N N 是 i i i 在 D D D 中可能的类别数(好瓜), N i N_i Ni 是第 i i i 个属性可能的取值数(其他属性,同 N j N_j Nj), D c , x i D_{c,x_i} Dc,xi 是类别为 c c c 且在第 i i i 个属性上取值为 x i x_i xi 的样本集合, D c , x i , x j D_{c,x_i,x_j} Dc,xi,xj 是类别为 c c c 且在第 i i i 和 第 j j j 个属性上取值分别为 x i x_i xi 和 x j x_j xj 的样本集合。例如,对西瓜数据集3.0有:
P ^ 是 , 浊 响 = P ( 好 瓜 = 是 , 敲 声 = 浊 响 ) ^ = 6 + 1 17 + 2 × 3 = 0.304 \hat{P}_{是,浊响}=\hat{P(好瓜=是,敲声=浊响)}=\frac{6+1}{17+2\times 3}=0.304 P^是,浊响=P(好瓜=是,敲声=浊响)^=17+2×36+1=0.304
P ^ 凹 陷 ∣ 是 , 浊 响 = P ^ ( 脐 部 = 凹 陷 ∣ 好 瓜 = 是 , 敲 声 = 浊 响 ) = 3 + 1 6 + 3 = 0.444 \hat{P}_{凹陷|是,浊响}=\hat{P}(脐部=凹陷|好瓜=是,敲声=浊响)=\frac{3+1}{6+3}=0.444 P^凹陷∣是,浊响=P^(脐部=凹陷∣好瓜=是,敲声=浊响)=6+33+1=0.444
综上可知,AODE的训练过程也是“计数”,在训练数据集上对符合条件的样本进行计数的过程。与朴素贝叶斯分类器相似,AODE无需模型选择,既能通过预计算节省预测时间,也能采取懒惰学习方式在预计算时再进行计数,并且易于实现增量学习。
既然将属性条件独立性假设放松为独依赖假设可能获得泛化性能的提升,那么,能否通过考虑属性间的高阶依赖来进一步提升泛化性能呢?也就是说将前面开头的的独依赖假设 P ( c ∣ x ) ∝ P ( c ) ∏ i = 1 d P ( x i ∣ c , p a i ) P(c|x) \propto{P(c)}\prod^d_{i=1}P(x_i|c,pa_i) P(c∣x)∝P(c)∏i=1dP(xi∣c,pai) 中 p a i pa_i pai 替换为包含 k k k 个属性的集合,从而将 ODE拓展为 k k kDE。需注意的是,随着 k k k 的增加,准确估计概率 P ( x i ∣ y , p a i ) P(x_i|y,pa_i) P(xi∣y,pai) 所需的训练样本数量将以指数级增加。因此,若训练数据非常充分,泛化性能有可能提升;但在有限样本条件下,则又陷入估计高阶联合概率的泥沼。
3.5、贝叶斯网
属性值相互独立的条件成立时,朴素贝叶斯分类是比其他所有分类算法要精确的。然而在现实中,属性之间的依赖存在可能,于是各种属性之间就产生了错综复杂的关系网络,随后贝叶斯网就诞生了,它的背后还蕴含着图论的数学思想。
3.5.1、概念与组成
贝叶斯网(Bayesian network)也称“信念网”(belief network),它是一种图形模型(概率理论和图论相结合的产物),可用于描述随机变量之间的依赖关系,是一种将因果知识和概率知识相结合的信息表示框架。
网络中每一个节点表示一个随机变量,每一条边表示随机变量间的依赖关系,同时每个节点都对应一个条件概率表,用于描述该变量与父变量之间的依赖强度,也就是联合概率分布。
贝叶斯网络由网络结构和条件概率表两部分组成:
- 网络结构是一个有向无环图(Directed Acylic Grap, DAG),如下图所示,用来刻画属性之间的依赖关系。重要的是,有向图蕴含了条件独立性假设。贝叶斯网络规定图中每个节点 x i x_i xi,如果已知它的父节点,则 x i x_i xi 条件独立于它的所有非后代节点。

- 条件概率表(Conditional Probability Table,CPT),把各个节点与它的父节点关联起来,用来描述属性的联合概率分布。条件概率表可以用 P ( x i ∣ p a i ) P(x_i|pa_i) P(xi∣pai) 来描述,它表达了节点同其父节点的关系——条件概率。没有任何父节点的节点,它的条件概率为其先验概率。
含有 K K K 个节点的贝叶斯网络,联合概率分布等于每个节点给定父节点的条件概率的乘积:
P ( X ) = ∑ i = 1 K P ( x i ∣ p a i ) P(X)=\sum_{i=1}^KP(x_i|pa_i) P(X)=i=1∑KP(xi∣pai)
因此,上图的贝叶斯网络联合概率分布为:
P ( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ) P ( x 4 ∣ x 1 , x 2 , x 3 ) P ( x 5 ∣ x 1 , x 3 ) P ( x 6 ∣ x 4 ) P ( x 7 ∣ x 4 , x 5 ) P(x_1,x_2,x_3,x_4,x_5,x_6,x_7)=P(x_1)P(x_2)P(x_3)P(x_4|x_1,x_2,x_3)P(x_5|x_1,x_3)P(x_6|x_4)P(x_7|x_4,x_5) P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)
由此可见,贝叶斯网络可以表达属性的联合概率分布,并且使属性的联合概率求解过程大大简化。
3.5.2、结构
通过贝叶斯网络中三个节点之间的典型依赖关系,可以划分3种基本结构形式:
(1)Tail-to-Tail——同父结构
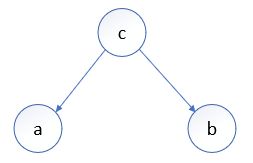
特点: 给定父节点 c c c 的取值,则 a a a与 b b b 条件独立,反之不独立。
证明:
根据贝叶斯网联合概率分布公式: P ( a , b , c ) = P ( c ) P ( a ∣ c ) P ( b ∣ c ) P(a,b,c)=P(c)P(a|c)P(b|c) P(a,b,c)=P(c)P(a∣c)P(b∣c),则:
- 当 c c c 作为条件已知时,因为: P ( a , b ∣ c ) = P ( a , b , c ) P ( c ) P(a,b|c)=\frac{P(a,b,c)}{P(c)} P(a,b∣c)=P(c)P(a,b,c),可得: P ( a , b ∣ c ) = P ( a , b , c ) P ( c ) = P ( c ) P ( a ∣ c ) P ( b ∣ c ) P ( c ) = P ( a ∣ c ) P ( b ∣ c ) P(a,b|c)=\frac{P(a,b,c)}{P(c)}=\frac{P(c)P(a|c)P(b|c)}{P(c)}=P(a|c)P(b|c) P(a,b∣c)=P(c)P(a,b,c)=P(c)P(c)P(a∣c)P(b∣c)=P(a∣c)P(b∣c),即当 c c c 已知时, a 、 b a、b a、b条件独立。
- 当 c c c 未知时, P ( a , b ) = ∑ c P ( a ∣ c ) P ( b ∣ c ) P ( c ) ≠ P ( a ) P ( b ) P(a,b)=\sum_cP(a|c)P(b|c)P(c)\neq P(a)P(b) P(a,b)=∑cP(a∣c)P(b∣c)P(c)=P(a)P(b),此时 a 、 b a、b a、b 不独立。
特点: 给定节点 c c c 的值,则 a a a 与 b b b 条件独立, 反之不独立。
证明:
根据贝叶斯网联合概率分布公式: P ( a , b , c ) = P ( a ) P ( c ∣ a ) P ( b ∣ c ) = P ( c ) P ( a ∣ c ) P ( b ∣ c ) P(a,b,c)=P(a)P(c|a)P(b|c)=P(c)P(a|c)P(b|c) P(a,b,c)=P(a)P(c∣a)P(b∣c)=P(c)P(a∣c)P(b∣c),则:
- 当 c c c 作为条件已知时,因为: P ( a , b ∣ c ) = P ( a , b , c ) P ( c ) P(a,b|c)=\frac{P(a,b,c)}{P(c)} P(a,b∣c)=P(c)P(a,b,c),可得: P ( a , b ∣ c ) = P ( a , b , c ) P ( c ) = P ( c ) P ( a ∣ c ) P ( b ∣ c ) P ( c ) = P ( a ∣ c ) P ( b ∣ c ) P(a,b|c)=\frac{P(a,b,c)}{P(c)}=\frac{P(c)P(a|c)P(b|c)}{P(c)}=P(a|c)P(b|c) P(a,b∣c)=P(c)P(a,b,c)=P(c)P(c)P(a∣c)P(b∣c)=P(a∣c)P(b∣c),即当 c c c 已知时,