C语言版，传教士与野人渡河问题，变态版，随便输入人数和船的最大载人数，人工智能经典题目，简单易懂，注释到位，没有bug

目录

一、问题描述

二、迟来的代码

运行截图

三、简单分析

一、问题描述

        有n个传教士和n个野人准备渡河，但只有一条能容纳c个人的小船，为了防止野人侵犯传教士，要求无论在何处，传教士的人数不得少于野人的人数(除非传教士人数为0)，且假定野人与传教士都会划船，试设计一个算法，确定他们能否渡过河去，若能，则给出小船来回次数最少的最佳方案。

二、迟来的代码

#include 
#include 

// 定义状态节点
typedef struct node
{
    int src_x;          // 起始岸传教士人数
    int src_y;          // 起始岸野人人数
    int dest_x;         // 目的岸传教士人数
    int dest_y;         // 目的岸野人人数
    int location;       // 船的状态，-1表示在目的岸，1表示在起始岸
    struct node *prev;  // 前指针
    struct node *next;  // 后指针
}node;

node *head;             // 状态链表的头节点
static int N = 0;       // 船的最大载人数
static int X = 0;       // 起始岸的传教士人数
static int Y = 0;       // 起始岸的野人人数
static int count = 0;   // 渡河方案

// 一些函数的声明
node *initList();
void del(node *new);
int checkSame(node *p);
void display(node *head);
int checkNo(int X, int Y);
void tail_insert(node *head, node *new);
void addnew(int x, int y, int location);
void Select(int X, int Y, int location);
void goRiver(int x, int y, int location);
int checkAll(int X, int Y, int location);

int main(void)
{
    head = initList();  // 初始化状态链表

    if(!head)
    {
        printf("初始化状态链表失败\n");
        return -1;
    }

    printf("请输入起始岸传教士人数:");
    scanf("%d", &X);

    printf("请输入起始岸野人人数:");
    scanf("\n%d", &Y);

    printf("请输入船的最大载人数:");
    scanf("\n%d", &N);

    // 把起始状态插入到链表中
    node *new = initList(); 
    new->src_x = X;
    new->src_y = Y;
    new->location = 1;
    tail_insert(head, new);

    printf("说明：渡河方案表示格式(起始岸传教士人数，起始岸野人人数，目的岸传教士人数，目的岸野人人数，船的状态）\n");
    printf("其中船的状态表示格式（-1表示船在目的岸，1表示船在起始岸）\n");
    printf("开始计算渡河方案\n");
    printf("计算中，请稍等...\n");

    Select(X, Y, 1);
    
    printf("渡河方案总共有%d种\n", count);

    return 0;
}

// 从起始岸或者目的岸选择人渡河，采用深度优先搜索法和剪枝回溯法
void Select(int X, int Y, int location)
{
    int x, y;
    // x, y满足以下三条不等式
    // x <= X 表示选择出的传教士人数不能超过岸上传教士的人数
    // y <= Y 表示选择出的野人人数不能超过岸上野人的人数
    // x + y <= N, 即y <= N - x, 表示选择出的总人数不能超过上船的最大载人数
    for(x = 0; x <= X; x++)
    {
        for(y = 0; y <= Y && y <= N-x; y++)
        {
            if((x == 0 && y > 0) || (x > 0 && x >= y)) 
            {
                // 如果是从起始岸选择，则必须至少选出2个人
                // 否则一个人划船没意思，会出现死循环
                if(location == 1 && x + y >= 2)
                {
                    goRiver(x, y, location);
                }
                // 如果是从目的岸选择，则必须保证选完人上船后，必须有人留在目的岸上
                // 否则从起始岸的划船到达目的岸没意思，会出现四循环
                if(location == -1 && head->prev->dest_x + head->prev->dest_y - x - y > 0)
                {
                    goRiver(x, y, location);
                } 
            }
        }
    }

    // 本次状态搜索完后，要回溯上一个分支(剪枝回溯法)
    if(head->next->next != head)
    {
        del(head->prev);
    }
}

// 判断从岸上选出的人能否渡河
void goRiver(int x, int y, int location)
{
    switch(checkAll(x, y, location))
    {
        // 不能渡河
        case 0:
            return;

        // 可以渡河
        case 1:
            addnew(x, y, location);

            // 需要进行转态查重
            // 具体例子是(2, 1, 0, 1, 1)->(0, 1, 2, 1, -1)->(2, 1, 0, 1, 1)->(0, 1, 2, 1, -1)...
            // 不去重会出现死循环，不信可以试试2个传教士，2个野人，船最大载人数为2的情况
            if(checkSame(head->prev))
            {
                del(head->prev);    // 删除重复的状态
                return;
            }

            // 全部已经渡河
            if(!head->prev->src_x && !head->prev->src_y)
            {
                printf("第%d种渡河方案\n", ++count);
                display(head);      // 打印渡河方案
                del(head->prev);    // 剪枝回溯
                return;
            }

            // 人还没全部渡河，且下一次从起始岸选择人渡河
            if(head->prev->location == 1)
            {
                Select(head->prev->src_x, head->prev->src_y, 1);
            }
            // 人还没全部渡河，且下一次从目的岸选择人渡河
            else
            {
                Select(head->prev->dest_x, head->prev->dest_y, -1);
            }

            return;

        // 已经全部渡河
        // 不过该条件基本不会出现, 因为case1中有判断下一个状态是否为目的态
        case 2:
            printf("第%d种渡河方案\n", ++count);
            display(head);      // 打印渡河方案
            del(head->prev);    // 剪枝回溯
            return;
    }
}

// 检查链表中是否有重复的状态
int checkSame(node *p)
{
    for(node *q = head->next; q != p; q = q->next)
    {
        // 只需要该状态的起始岸或者目的岸的人数进行比较，不需要两个岸都要进行比较
        if(q->src_x == p->src_x && q->src_y == p->src_y && q->location == p->location)
        {
            return 1;
        }
    }

    return 0;
} 

// 检查在起始岸或者目的岸的人数是否合法
int checkNo(int x, int y)
{
    return x > 0 && x < y;
}

// 检查在起始岸和目的岸的人是否合法
int checkAll(int x, int y, int location)
{
    int src_x, src_y, dest_x, dest_y;
    src_x = head->prev->src_x;
    src_y = head->prev->src_y;
    dest_x = head->prev->dest_x;
    dest_y = head->prev->dest_y;

    // 只要起始岸或者目的岸的人数不合法，就不能渡河
    if(checkNo(src_x - x * location, src_y - y * location) 
        || checkNo(dest_x + x * location, dest_y + y * location))
        {
            return 0;
        }

    // 已经全部渡河，不需要再渡河
    else if(location == -1 && src_x == 0 && src_y == 0 && dest_x == X && dest_y == Y)
    {
        return 2;
    }

    // 本次选择的人可以渡河，但未全部渡河
    else
    {
        return 1;
    }
}

// 把新的状态插入到链表中
void addnew(int x, int y, int location)
{
    node *p = initList();

    if(!p)
    {
        printf("malloc fail\n");
        return;
    }

    // 修改状态的信息
    // 有个小技巧，关于location的，不需要分起始岸或者目的岸写
    p->src_x = head->prev->src_x - x * location;
    p->src_y = head->prev->src_y - y * location;
    p->dest_x = head->prev->dest_x + x * location;
    p->dest_y = head->prev->dest_y + y * location;
    p->location = -head->prev->location;
    
    tail_insert(head, p);
}

// 生成一个状态节点
node *initList()
{
    node *new = malloc(sizeof(node));

    if(!new)
    {
        printf("malloc fail!\n");
        return NULL;
    }

    new->src_x = 0;
    new->src_y = 0;
    new->dest_x = 0;
    new->dest_y = 0;
    new->location = 0;
    new->prev = new;
    new->next = new;

    return new;
}

// 打印渡河方案
void display(node *head)
{
    // 链表不存在或者为空
    if(!head || head->next == head)
    {
        return;
    }

    for(node *p = head->next; p != head; p = p->next)
    {
        printf("%d, %d, %d, %d, %d\n", p->src_x, p->src_y, p->dest_x, p->dest_y, p->location);
    }

    printf("\n");
}

// 尾插法，把节点插到链表最末
void tail_insert(node *head, node *new)
{
    new->prev = head->prev;
    new->next = head;
    head->prev->next = new;
    head->prev =new;
}

// 删除一个节点，本程序通常是链表最末的一个
void del(node *new)
{
    new->prev->next = new->next;
    new->next->prev = new->prev;
    new->prev = new;
    new->next = new;
    free(new);
}

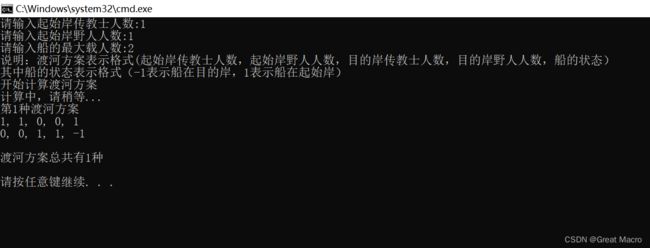
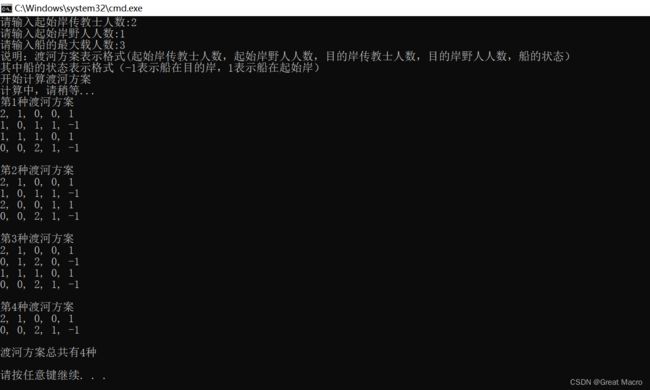
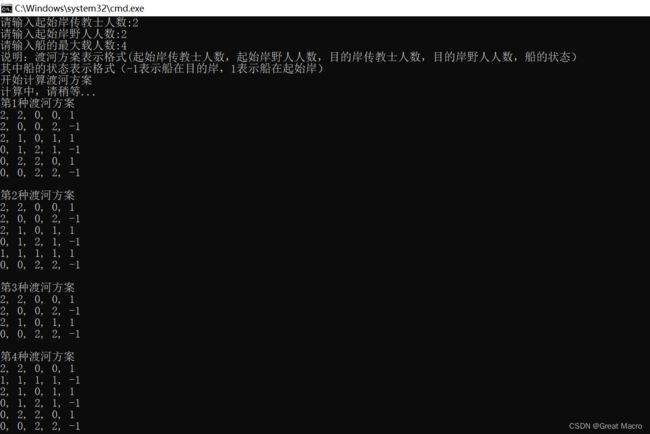
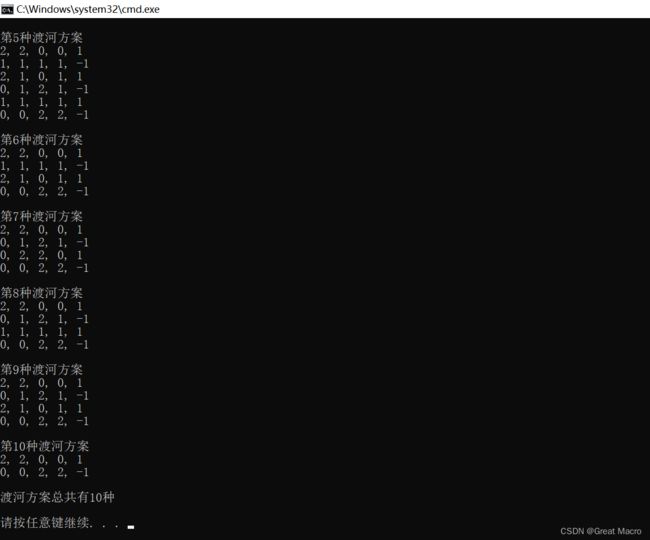
运行截图

 

三、简单分析

        如果你认真看完代码和对应的注释，相信心中觉得其实这个也不算很难，但是可以找到别的博主写的传教士与野人渡河问题的博客，我不太容易看懂，特别是对于初学者来说，而且写的也有局限性。比如说，他们规定了船的最大载人数为2，甚至直接写死了传教士和野人的人数。虽然这么写很好写，很方便，但是不利于我们锻炼编程思维和能力，而且这样写多多少少不太算人工智能，毕竟都写死了嘛^_^

        主要关键易错点：

1、分三步判断人数是否合法。先从岸上选择合适的人数上船，然后判断选择后起始岸（目的岸）的人数是否合法，渡河后目的岸（起始岸）的人数是否合法。

2、注意有合法但是无意义的渡河操作。比如说，从起始岸只选择出一个人渡河，这样的选择无意义，因为船要从目的岸划回来，而划回来就至少需要一个人，所有本次选择无意义，一个人划来划去，没意思，而且会出现死循环。在比如，从目的岸选择人划船回来后，目的岸没有人留下。因为这样操作，相当于没有人渡河了，还不如不做，而且会出现死循环。

3、注意可能会有状态重复的情况。比如说，从两个传教士和野人要渡河且船的最大载人数为2时，就会出现重复情况。如果不是调试和画图，这个易错点真的无法发现。如图

 4、对链表的操作不熟悉。如果你看不懂双向循环链表的操作，可以在我的博客里找，绝对包你看得满意，看得明白。

5、不要介意用什么语言。C语言好，还是C++，或者Java，Python等。选择一种自己熟悉的就行。

温馨提示：

        如果在运行程序时，觉得是死循环，不用慌，其实不是，可能是电脑配置低了嗲=点，也可能是本次渡河方案有好几万种，稍微喝个水，休息一下，就好了^_^。而且不是所有的情况都有解的，比如说，当船的最大载人数为2时，传教士和野人人数都为4，5，6等时，就无解。

四、小小总结

        如果觉得我写的还不错的话，可以点赞加关注，博主的博客力求精益求精，还有一猴子摘香蕉的题目。至于创作的原因，很简单，就是自己在看别人写的博客，觉得不是很好，就自己动手尝试写活了，感兴趣的可以看看博主写的猴子摘香蕉，你几乎找不到第二个跟我的是一样的思路的。

        本期国庆礼包就到了，下期再见。（博客里有你可能需要的实验报告^_^）

---