【读书笔记】《深入浅出图神经网络——GNN原理解析》

0. 前言

《深入浅出图神经网络——GNN原理解析》这本书是目前关于图神经网络的第一本中文图书。书上更多地是从数学的角度来解释GNN的原理，对程序的编写和理解更有帮助，个人觉得从数学的角度去理解更有意思。可以结合cs224w来看，cs224w是从实际的社交网络出发逐渐讲到图神经网络，两个视角结合来看比较有趣。

书中的1-4章是一些基础概念，第五章开始和图神经网络相关。

《深入浅出图神经网络：GNN原理解析》配套代码：GraphNeuralNetwork

书的链接：深入浅出图神经网络：GNN原理解析

1. 图信号处理与图卷积神经网络

第五章《图信号处理与图卷积神经网络》可以结合cs224w的Spectral Clustering（cs224w 图神经网络 学习笔记（六）Spectral Clustering 谱聚类）这节课来看。

1.1 图信号与图的拉普拉斯矩阵

书中提到的图信号处理实质上就是Node2Vec。

图信号是一种描述$V\to R$的映射，表示成向量的形式：$\mathbf{x}=[x_1,x_2,\cdots ,x_N{]}^T$，其中$x_i$表示的是节点$v_i$上的信号强度。

拉普拉斯矩是图论中的一个重要的矩阵，作为一个图的矩阵表示。其定义为$L=D-A$，其中$D_{ii}={\sum }_j{A}_{ij}$为图的度矩阵，$A$为图的邻接矩阵。即

$$L_{ij}=\{\begin{array}{ll}deg(v_i),& \text{if i=j}\\ -1,& \text{if eij∈E}\\ 0,& \text{otherwise}\end{array}$$

显然，拉普拉斯矩阵是对称的。此外，拉普拉斯矩阵还有一种正则化的形式（symmetric normalized laplacian）$L_{sym}=D^{-1/2}L{D}^{-1/2}$，元素级别的定义如下：

$$L_{sym}[i,j]=\{\begin{array}{ll}1,& \text{if i=j}\\ \frac{-1}{\sqrt{deg(v_i)deg(v_j}},& \text{if eij∈E}\\ 0,& \text{otherwise}\end{array}$$

当涉及到信号处理或者图论的时候，就避不开拉普拉斯矩阵。拉普拉斯矩阵的定义来源于拉普拉斯算子。关于为什么拉普拉斯矩阵的定义式如上所述，以及为什么拉普拉斯矩阵常用于无向图，可以看这篇文章：【其实贼简单】拉普拉斯算子和拉普拉斯矩阵。对于一个函数，拉普拉斯算子实际上衡量了在空间中的每一点处，该函数梯度是倾向于增加还是减少。

对于图中的每个节点来说：

$$L\mathbf{x}=(D-A)\mathbf{x}=[\cdots ,\sum _{v_j\in N(v_i)}(x_i-x_j),\cdots ]$$

也就是说，拉普拉斯矩阵式一个反映图信号局部平滑度的算子。

同时，可以定义一个重要的二次型：

$$TV(\mathbf{x})={\mathbf{x}}^{T}L\mathbf{x}=\sum _{v_i}\sum _{v_j\in N(v_i)}{x}_i(x_i-x_j)=\sum _{e_{ij}\in E}(x_i-x_j{)}^2$$

称$TV(\mathbf{x})$为图信号的总变差（Total Variantion），刻画的是图信号整体的平滑度。

1.2 傅里叶变换

这一部分实质上是对cs224w课程Spectral Clustering的一些从数学角度上的补充，图傅里叶变换是图谱分析的基础。

时域和频域

时域和频域是信号的基本性质。时域（Time domain）是描述数学函数或物理信号对时间的关系。频域（frequency domain）是描述信号在频率方面特性时用到的一种坐标系。相对于更加直观的时域视角，频域分析则更能体现信号的一些特征和本质。

傅里叶变换则是将信号从时域空间转换到频域空间的方法，是数字信号处理的基石。类比傅里叶变换，书中首先给出图信号傅里叶变换的定义，即将图信号由空域（spatial domain）视角转换成频域视角。在我们得到图信号（这个图信号可以看做是空域视角）的时候，我们就需要进行频域分析（我们需要切换到频域视角来观察图信号的特征），得到图的谱，进而进行谱聚类等操作。

拉普拉斯矩阵的一些性质

由于拉普拉斯矩阵是一个实对称矩阵，它可以被正交对角化表示为

$$L=V\Lambda V^T=\left[\begin{array}{cccc}⋮& ⋮& \cdots & ⋮\\ {\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_N\\ ⋮& ⋮& \cdots & ⋮\end{array}\right]\left[\begin{array}{ccccc}{\lambda }_1& & & & \\ & {\lambda }_2& & & \\ & & \ddots & & \\ & & & & {\lambda }_N\end{array}\right]\left[\begin{array}{ccc}\cdots & {\mathbf{v}}_1& \cdots \\ \cdots & {\mathbf{v}}_2& \cdots \\ \cdots & ⋮& \cdots \\ \cdots & {\mathbf{v}}_N& \cdots \end{array}\right]$$

其中$V$是一个正交矩阵，即$V{V}^T=I$。$V=[{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_N]$为$L$的$N$个特征向量，这些特征向量都是彼此之间线性无关的单位向量。${\lambda }_k$表示第$k$个特征向量对应的特征值，并对特征值进行升序排列，即${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_N$。

同时，可以得到以下性质：

1. 由于$TV(\mathbf{x})={\sum }_{e_{ij}\in E}(x_i-x_j{)}^2\ge 0$，因此拉普拉斯矩阵为半正定型矩阵，因此其所有的特征子均大于等于零。
2. 由于$L\mathbf{x}=(D-A)\mathbf{x}=[\cdots ,{\sum }_{v_j\in N(v_i)}(x_i-x_j),\cdots ]$，所以$LI=0$，因此拉普拉斯矩阵拥有最小的特征值0，即${\lambda }_1=0$。
3. 同时可以证明，对于$L_{sym}$，其特征值存在一个上限：${\lambda }_N\le 2$。

图傅里叶变换（Graph Fourier Transform, GFT）

定义：对于任意一个在图G上的信号$x$，其图傅里叶变换为

$${\tilde{x}}_k=\sum _{i=1}^N{V}_{ki}^T{x}_i=⟨v_k,\mathbf{x}⟩$$

其中$v_k$为拉普拉斯的第$k$个特征向量，成为傅里叶基；${\tilde{x}}_k$是$\mathbf{x}$在第$k$个傅里叶基上的傅里叶系数。本质上来说，傅里叶系数是图信号在傅里叶基上的投影，衡量了图信号与傅里叶基之间的相似度。

将上式写成矩阵形式：

$$\tilde{\mathbf{x}}=V^T\mathbf{x},\tilde{\mathbf{x}}\in R^N$$

又$V\tilde{\mathbf{x}}=V{V}^T\mathbf{x}=I\mathbf{x}=\mathbf{x}$，所以

$$\mathbf{x}=V\tilde{\mathbf{x}}，\mathbf{x}\in R^N$$

可以将上式代入到总变差$TV(\mathbf{x})$的式子，得到

$$\begin{array}{rl}TV(\mathbf{x})& ={\mathbf{x}}^{T}L\mathbf{x}={\mathbf{x}}^{T}V\Lambda V^T\mathbf{x}\\ & =(V\tilde{\mathbf{x}}{)}^{T}V\Lambda V^T(V\tilde{\mathbf{x}})\\ & ={\tilde{\mathbf{x}}}^T{V}^{T}V\Lambda V^{T}V\tilde{\mathbf{x}}\\ & ={\tilde{\mathbf{x}}}^T\Lambda \tilde{\mathbf{x}}\\ & =\sum _k^N{\lambda }_k{\tilde{x}}_k^2\end{array}$$

即$TV(\mathbf{x})={\sum }_k^N{\tilde{x}}_k^2{\lambda }_k$，总变差是图的所有特征值的一个线性组合，权重是图信号相对应的傅里叶系数的平方。因此，对于一个给定的图，总变差取最小值的条件是：图信号与最小的特征值${\lambda }_1$所对应的特征向量$v_1$完全重合，此时仅有$x_1\ne 0$，其他项的傅里叶系数为0，总变差$TV(\mathbf{x})={\lambda }_1$。事实上，可以进一步证明，如果图信号$\mathbf{x}={\mathbf{v}}_k$，则总变差$TV(\mathbf{x})={\lambda }_k$。前面提到，总变差刻画的是图信号的整体平滑度，那么将特征值依次排序，相当于对图信号的平滑度做出了一种梯度刻画，因此，可以将特征值等价成频率——特征值越低，频率越低，对应的傅里叶基变化的越缓慢，相近节点上的信号值趋于一致；特征值越高，频率越高，对应的傅里叶基就变化的越剧烈，相近节点上的信号值则非常不一致。

我们进而可以定义图信号的能量，图信号的能量可以同时从空域和频域进行等价定义：

$$E(\mathbf{x})=||\mathbf{x}|{|}_2^2={\mathbf{x}}^T\mathbf{x}=(V\tilde{\mathbf{x}}{)}^T(V\tilde{\mathbf{x}})={\tilde{\mathbf{x}}}^T{V}^{T}V\tilde{\mathbf{x}}={\tilde{\mathbf{x}}}^T\tilde{\mathbf{x}}$$

结合上述书上的内容，可以对维基百科中对于图傅里叶变换的定义理解的更加清楚：In mathematics, graph Fourier transform is a mathematical transform which eigendecomposes the Laplacian matrix of a graph into eigenvalues and eigenvectors. Analogously to classical Fourier Transform, the eigenvalues represent frequencies and eigenvectors form what is known as a graph Fourier basis.（从数学上看，图的傅里叶变换是对图的拉普拉斯矩阵进行频谱分析，得到特征值和特征向量。与传统的傅里叶分析类似，频谱分析得到的特征值代表频率，特征向量代表图的傅里叶基。）

那么，傅里叶系数可以看做是对应特征向量（傅里叶基）上的幅值，反映图信号在该频率分量上的强度。图信号在低频分量上的强度越大，该信号的平滑度越高；图信号在高频分量上的强度越大，该信号平滑度越低。

将图的所有傅里叶系数合在一起，就可以得到图的频谱（spectrum），这个频谱完整地描述了图信号的频域特性，就相当于是图的一种身份ID。

---

到这里，我们就可以更好地去理解Spectral Clustering（cs224w 图神经网络 学习笔记（六）Spectral Clustering 谱聚类）课程中的思想。

谱聚类有三个基本的步骤：

（1）Pre-processing 预处理

• Construct a matrix representation of the graph 构造图的矩阵表示
  
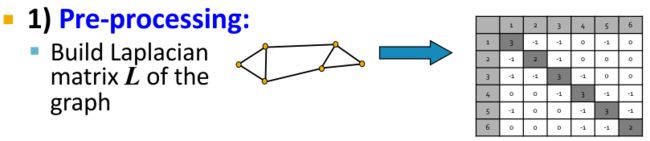
  第一步就是构建拉普拉斯矩阵。

（2）Decomposition 分解

• Compute eigenvalues and eigenvectors of the matrix 计算矩阵的特征值和特征向量
• Map each point to a lower-dimensional representation based on one or more eigenvectors 将每个点映射到一个低维向量
  
  第二步就是进行图傅里叶变换，也就是进行频谱分析，得到拉普拉斯矩阵的特征值和特征向量。

（3）Grouping 聚类

• Assign points to two or more clusters, based on the new representation 根据降维后的向量进行分组

结合总变差的意义，就可以理解为什么可以选用第k个特征值对应的特征向量来作为节点的标签，然后进行聚类了。

如果图信号$\mathbf{x}={\mathbf{v}}_k$，则总变差$TV(\mathbf{x})={\lambda }_k$。

那么，怎么确定选择第几个特征向量呢？

课程中也给出了方法——通过两个连续的特征值之间的差来确定。

前面提到，$\lambda$值可以等价于频率，$\lambda$值越低，信号值越趋于一致——这显然不符合我们聚类的想法，聚类就是为了将信号值不一样的节点进行归类。那么，当信号值发生抖动时，$\lambda$值就会变大，因此，我们找到$\lambda$差值最大的一组特征向量作为聚类选择的依据——这意味着图信号可能从相对一致的状态下（较小的$\lambda$值对应的特征向量）发生了质变。

那么根据特征向量（图信号），就可以自然而然地进行聚类了。

---

1.3 图滤波器（Graph Filter）

定义：对给定图信号的频谱中各个频率分量的强度进行增强或衰减的操作。

设图滤波器为$H\in R^{N\times N}$，$H:R^N\to R^N$，令输出图信号为$\mathbf{y}$，则

$$\mathbf{y}=H\mathbf{x}=\sum _{k=1}^N(h({\lambda }_k){\tilde{x}}_k){\mathbf{v}}_k$$

可以看出，图滤波器实质上是通过控制$h(\lambda )$项来进行增强或者衰减的。将上式写成矩阵形式

$$\begin{array}{rl}\mathbf{y}& =H\mathbf{x}=\sum _{k=1}^N(h({\lambda }_k){\tilde{x}}_k){\mathbf{v}}_k\\ & =\left[\begin{array}{cccc}⋮& ⋮& \cdots & ⋮\\ {\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_N\\ ⋮& ⋮& \cdots & ⋮\end{array}\right]\left[\begin{array}{c}h({\lambda }_1){\tilde{x}}_1\\ h({\lambda }_2){\tilde{x}}_2\\ ⋮\\ h({\lambda }_N){\tilde{x}}_N\end{array}\right]\\ & =V\left[\begin{array}{cccc}h({\lambda }_1)& & & \\ & h({\lambda }_2)& & \\ & & \ddots & \\ & & & h({\lambda }_N)\end{array}\right]\left[\begin{array}{c}{\tilde{x}}_1\\ {\tilde{x}}_2\\ ⋮\\ {\tilde{x}}_N\end{array}\right]\\ & =V\left[\begin{array}{cccc}h({\lambda }_1)& & & \\ & h({\lambda }_2)& & \\ & & \ddots & \\ & & & h({\lambda }_N)\end{array}\right]V^T\mathbf{x}\end{array}$$

于是，得到

$$H=V\left[\begin{array}{cccc}h({\lambda }_1)& & & \\ & h({\lambda }_2)& & \\ & & \ddots & \\ & & & h({\lambda }_N)\end{array}\right]V^T=V{\Lambda }_h{V}^T$$

相较于拉普拉斯矩阵，$H$仅仅改动了对角矩阵上的值。

图滤波器的性质

1. 线性——$H(\mathbf{x}+\mathbf{y})=H\mathbf{x}+H\mathbf{y}$
2. 顺序无关——$H_1(H_2\mathbf{x})=H_2(H_1\mathbf{x})$
3. 如果$h(\lambda )\ne 0$，则该滤波操作是可逆的。

三种滤波器

称${\Lambda }_h$为滤波器$H$的频率响应矩阵，对应的函数$h(\lambda )$为$H$的频率响应函数，不同的频率响应函数有不同的滤波效果。

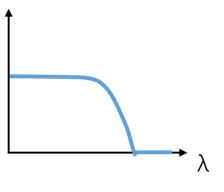
低通滤波器	高通滤波器	带通滤波器
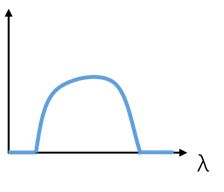只保留图信号中的低频部分，更关注信号中平滑的部分	只保留信号中的高频部分，更关注信号中快速变化的部分	只保留信号中特定频段的部分

如果我们想要实现任意性质的图滤波器，可以用泰勒展开，得到

$$H=h_0{L}^0+h_1{L}^1+h_2{L}^2+\cdots +h_K{L}^K=\sum _{k=0}^K{h}_k{L}^k$$

其中$K$是图滤波器$H$的阶数。

从空域视角理解图滤波器

对于$\mathbf{y}=H\mathbf{x}={\sum }_{k=0}^K{h}_k{L}^k\mathbf{x}$，若假设${\mathbf{x}}^{(k)}=L^k\mathbf{x}=L{\mathbf{x}}^{(k-1)}$，那么$\mathbf{y}={\sum }_{k=0}^K{\mathbf{h}}^k{\mathbf{x}}^{(k)}$，也就是说，经过滤波器操作的输出图信号编程了$(K+1)$组图信号的线性加权。

从空域视角来看，滤波操作具有以下性质：

1. 局部性——每个节点的输出信号值只需要考虑其K阶子图；
2. 可以通过K步迭代式的矩阵向量乘法来完成滤波操作。

从频域视角理解图滤波器

将$L=V\Lambda V^T$代入$H={\sum }_{k=0}^K{h}_k{L}^k$，得到

$$\begin{array}{rl}H& =\sum _{k=0}^K{h}_k(V\Lambda V^T{)}^k=V(\sum _{k=0}^K{h}_k{\Lambda }^k)V^T\\ & =V\left[\begin{array}{ccc}{\sum }_{k=0}^K{h}_k{\lambda }_1^k& & \\ & \ddots & \\ & & {\sum }_{k=0}^K{h}_k{\lambda }_N^k\end{array}\right]V^T\end{array}$$

那么，应用滤波器进行滤波，则$\mathbf{y}=H\mathbf{x}=V({\sum }_{k=0}^K{h}_k{\Lambda }^k)V^T\mathbf{x}$

由此可以得到频域视角下的滤波操作：

1. 通过图傅里叶变换$V^T\mathbf{x}$将图信号变换到频域空间
2. 通过${\Lambda }_h={\sum }_{k=0}^K{h}_k{\Lambda }^k$对频率分量的强度进行调节，得到$\tilde{\mathbf{y}}$；
3. 通过逆图傅里叶变换$V\tilde{\mathbf{y}}$将$\tilde{\mathbf{y}}$反解成图信号$\mathbf{y}$。

假设滤波器$H$经过泰勒展开后的多项式系数$h$构成向量$\mathbf{h}$，则$H$的频率响应矩阵为

$${\Lambda }_h=\sum _{k=0}^K{h}_k{\Lambda }^k=diag(\Psi \mathbf{h})$$

其中$\Psi =\left[\begin{array}{cccc}1& {\lambda }_1& \cdots & {\lambda }_1^K\\ 1& {\lambda }_2& \cdots & {\lambda }_2^K\\ ⋮& ⋮& \ddots & ⋮\\ 1& {\lambda }_N& \cdots & {\lambda }_N^K\end{array}\right]$为范德蒙矩阵。同理可以反解得到多项式系数：$\mathbf{h}={\Psi }^{-1}dia{g}^{-1}({\Lambda }_h)$。这样一来，我们就可以设计具有特定性质的图滤波器。

从频域视角来看，图滤波操作具有以下特点：

1. 从频域视角能够更加清晰地完成对图信号的特定滤波操作；
2. 图滤波器如何设计具有显示的公式指导；
3. 对矩阵进行特征分解的时间复杂度为$O(N^3)$，相比空域视角中的矩阵向量乘法而言，有工程上的局限性。

1.4 图卷积神经网络

图卷积运算的定义如下：

$$x_1\ast x_2=IGFT(GFT(x_1)\odot GFT(x_2))$$

其中$\odot$表示哈达玛积，$GFT$表示傅里叶变换。将$GFT(\mathbf{x})=\tilde{\mathbf{x}}=V^T\mathbf{x}$代入上式，得到

$$\begin{array}{rl}{x}_1\ast x_2& =V((V^T{\mathbf{x}}_1)\odot (V^T{\mathbf{x}}_2))=V({\tilde{\mathbf{x}}}_1\odot (V^T{\mathbf{x}}_2))\\ & =V(diag({\tilde{\mathbf{x}}}_1)(V^T{\mathbf{x}}_2))\\ & =(Vdiag({\tilde{\mathbf{x}}}_1)V^T){\mathbf{x}}_2\end{array}$$

令$H_{{\tilde{\mathbf{x}}}_1}=Vdiag({\tilde{\mathbf{x}}}_1)V^T$，则$x_1\ast x_2=H_{{\tilde{\mathbf{x}}}_1}{x}_2$。显然，$H_{{\tilde{\mathbf{x}}}_1}$是一个图位移算子，其频率响应矩阵为${\mathbf{x}}_1$的频谱；也就是说，图卷积等价于图滤波。

那么，我们可以定义如下神经网络层对频率响应矩阵尽心参数化：

$$\begin{array}{rl}{X}^{\prime }& =\sigma (V\left[\begin{array}{cccc}{\theta }_1& & & \\ & {\theta }_2& & \\ & & \ddots & \\ & & & {\theta }_N\end{array}\right]V^{T}X)\\ & =\sigma (Vdiag(\theta )V^{T}X)\\ & =\sigma (\Theta X)\end{array}$$

其中$\sigma (\cdot )$是激活函数，$\theta =[{\theta }_1,{\theta }_2,\cdots ,{\theta }_N]$是需要学习的参数，$\Theta$是需要学习的图滤波器，$X$是输入的图信号矩阵，$X^{\prime }$是输出的图信号矩阵。

从空域视角来看，定义的这个神经网络层引入了一个自适应的图位移算子；从频域视角来看，该神经网络层在$X$和$X^{\prime }$之间训练了一个可自适应的图滤波器，其频率响应函数可以通过任务与数据之间的对应关系来进行监督学习。

不过，需要注意的是，在真实的图数据中，数据的有效信息通畅都蕴含在低频段中，因此一般会为图滤波器设置N个维度的自由度。

为了拟合任意的频率响应函数，论文Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering将拉普拉斯矩阵$Vdiag(\theta )V^T$的多项式形式转换成一种可以学习的形式：

$$X^{\prime }=\sigma (V(\sum _{k=0}^K{\Lambda }^k)V^{T}X)=\sigma (Vdiag(\Psi \theta )V^{T}X)$$

同样的，$\theta =[{\theta }_1,{\theta }_2,\cdots ,{\theta }_N]$是需要学习的参数；不同的是这个方法的参数量$K$可以自由控制。$K$越大，可拟合的频率响应函数的次数就越高，可以对应输入图信号矩阵与输出图信号矩阵之间复杂的滤波关系；反之就越简单。一般来说，会设$K<<N$以降低模型过拟合的风险。

为了进一步简化矩阵特征分解的计算复杂度，论文Semi-supervised classification with graph convolutional networks中限制$K=1$，则

$$X^{\prime }=\sigma ({\theta }_{0}X+{\theta }_{1}LX)$$

令${\theta }_0={\theta }_1=\theta$，则

$$X^{\prime }=\sigma (\theta (I+L)X)=\sigma (\theta \tilde{L}X)$$

设$\theta =1$，则$X^{\prime }=\sigma (\tilde{L}X)$，也就是说，我们可以通过一个固定的图滤波器$\tilde{L}$，哎进行图卷积操作。

定义${\tilde{L}}_{sym}$为重归一化形式的拉普拉斯矩阵，${\tilde{L}}_{sym}$的特征值范围为$(-1,1]$，${\tilde{L}}_{sym}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}$，其中$\tilde{A}=A+I$，${\tilde{D}}_{ij}={\sum }_j{\tilde{A}}_{ij}$。同时，定义一个参数化的权重矩阵$W$对输入的图信号矩阵进行仿射变换，则可以得到图卷积层的数学表达，以此为主体堆叠多层的神经网络模型称为图卷积模型（GCN）：

$$X^{\prime }=\sigma ({\tilde{L}}_{sym}XW)$$

2. GCN实战

【深度学习实战】《深入浅出图神经网络》GCN实战（pytorch）

3. 图卷积层的数学表达

关于图卷积层的数学表达，结合cs224w课程中的思路，理解起来更加清晰。

$X^{\prime }=\sigma ({\tilde{L}}_{sym}XW)$实质上可以看成两步，第一步$XW$是对属性信息的f仿射变换，学习属性特征之间的交互模式；第二步${\tilde{L}}_{sym}(XW)$是聚合邻居节点的过程，代表了对节点局部结构信息的编码。

4. GraphSAGE

实际上cs224w 图神经网络 学习笔记（九）Graph Neural Networks 图神经网络课程中提到的图神经网络模型的思想是GraphSAGE的“聚合邻居（aggregation）”的思想，从两个方面将图卷积神经网络模型$X^{\prime }=\sigma ({\tilde{L}}_{sym}XW)$进行了简化：

1. 通过采用邻居的策略，将GCN由全图（full batch）的训练方式变成以节点为中心的小批量（mini batch）的方式。
2. 对聚合邻居的操作提出了扩展，提出了替换GCN操作的几种新方式。

相关论文：

论文	简介
Inductive Representation Learning on Large Graphs	理论的提出
1. FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling 2. Adaptive Sampling Towards Fast Graph Representation Learning 3. Stochastic Training of Graph Convolutional Networks with Variance Reduction	GraphSAGE选择的了均匀分布，事实上根据工程效率或者数据的业务背景，我们可以采用其他形式的分布来代替。
Graph Convolutional Neural Networks for Web-Scale Recommender Systems	基于GraphSAGE的工业级大规模推荐系统的应用

GraphSAGE算法的计算过程完全没有拉普拉斯矩阵的参与，每个节点的特征学习过程仅仅只与其k阶邻居相关，而不需要考虑全图的结构信息。这样的方法适合做归纳学习（Inductive Learning），这是指可以对在训练阶段见不到的数据直接进行预测而不需要重新训练的学习方法——这也使得GraphSAGE有着很高的推广和应用价值。与之对应的是转导学习（Transductive Learning），指所有的数据在训练阶段都可以拿到，学习过程是作用在这个固定的数据上的，一旦数据发生改变，需要重新进行学习训练，如随机游走算法。