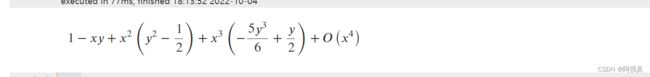python计算微积分

python计算微积分

本文将使用sympy库计算微积分pip install sympy

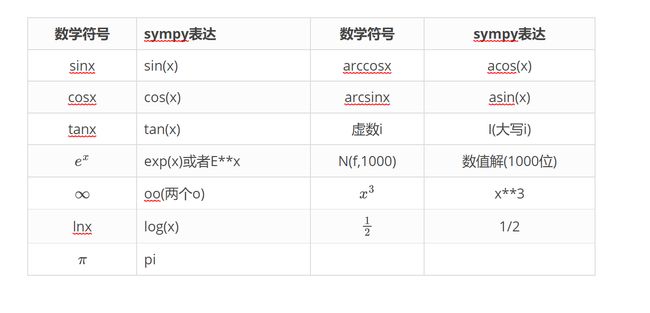
符号说明： 默认导入库的方式为from sympy import *

一.计算极限

limit(f,x,h)f是表达式，x是对谁求极限，h是x趋于多少
$$\underset{x\to 0}{\lim }\frac{\sin x-\tan x+e^{\tan x}-1}{x-\tan x+\sin x}$$

from sympy import *
x=Symbol("x")
f=(sin(x)-tan(x)+exp(tan(x))-1)/(x-tan(x)+sin(x))
limit(f,x,0)#如果没有输出结果请print(limit(f,x,0))

输出结果为1

二.求导数

1.求一阶导数

$$求x^4+x^3+x+1的一阶导数$$

from sympy import *
x=Symbol("x")
expr=x**4+x**3+x+1
expr.diff(x)#注意如果没有输出任何内容，请使用print(expr.diff(x)),以下同理

2.求高阶导数

​
$$求\sin x的100阶导数$$

from sympy import *
x=Symbol("x")
expr=sin(x)
expr.diff(x,100)

3.多元函数求导

$$\begin{gathered} f\left(x,y\right)={\left(x+1\right)}^3{y}^2\left(z-1\right)\left(\text{其中}z\text{是常数}\right) \\ \text{求}:\frac{{\partial }^{2}f\left(x,y\right)}{\partial x\partial y} \end{gathered}$$

#多元函数
from sympy import *
x=Symbol("x")
y=Symbol('y')
z=Symbol("z")
expr=(x+1)**3*y**2*(z-1)
expr.diff(x,y)

4.多元函数求高阶导数

$$\begin{gathered} f\left(x,y\right)={\left(x+1\right)}^3{y}^2\left(z-1\right)\left(\text{其中}z\text{是常数}\right) \\ \text{求}:\frac{{\partial }^{3}f\left(x,y\right)}{\partial x^2\partial y} \end{gathered}$$

from sympy import *
x=Symbol("x")
y=Symbol('y')
z=Symbol("z")
expr=(x+1)**3*y**2*(z-1)
expr.diff(x,2,y,1)#注意这里2和1的位置

三.计算积分

1.不定积分

$$\text{计算}\int x^5\sin xdx$$

from sympy import *
x=Symbol("x")
expr=x**5*sin(x)
integrate(expr,x)#如果输出为空，就换为print(integrate(expr,x))

2.计算定积分

$${\int }_0^{\infty }\ln x\sin xdx$$

无穷大的表示：oo(没错就是两个o)

​

from sympy import *
x=Symbol("x")
expr=log(x)*sin(x)
integrate(expr,(x,0,oo))

抱歉，他不收敛,返回我输入的表达式了，我们换一个

计算：${\int }_0^{\infty }a\sin \left(x\cos x\right)dx$，其中a为常数

呃呃呃，这个有点难算，又返回原函数了，但是这个是发散的吗？

我有点不服啊，掏出我的Wolfram Mathematic试试，好吧，咱也看不懂，总之就是这样计算的

3.计算二重积分

$$\iint \left(x+\sin y\right)e^{x}dxdy$$

from sympy import *
x=Symbol("x")
y=Symbol("y")
expr=(x+sin(y))*exp(x)
integrate(expr,x,y)

$$ \int_0^1{\int_0^1{\left( x+\sin y \right) e^xdxdy}} $$

from sympy import *
x=Symbol("x")
y=Symbol("y")
expr=(x+sin(y))*exp(x)
integrate(expr,(x,0,1),(y,0,1))

四.级数展开

$$\cos x\text{在}x=0\text{处}3\text{阶展开}$$

from sympy import *
x=Symbol("x")
cos(x).series(x,0,n=3)#偶数项展开为0，所以只有两项

我们可以不写后面的0和n，因为默认是在0处展开：

$e^x$的泰勒展开

from sympy import *
x=Symbol("x")
# cos(x).series(x,0,n=3)
exp(x).series(x)

任意表达式的展开

$$f\left(x\right)=\frac{\cos \left(x\right)}{1+\sin \left(xy\right)}\text{在}x=0\text{处展开四阶}$$

from sympy import *
x,y=symbols("x,y")#注意这里是symbols
expr=cos(x)/(1+sin(x*y))
expr.series(x,n=4)