有营养的算法笔记(二)
有营养的算法比较二
-
- 最短距离
- 4键键盘
- 冗余的边II
- 冗余的边
最短距离
1.本题为某公司的笔试题,所以没有这个测试链接。在这里只给出代码和思路。
2.题目描述
int n, int[][] roads, int x, int y,n表示城市数量,城市编号0~n-1
roads[i][j] == distance,表示城市i到城市j距离为distance(无向图)
求城市x到城市y的最短距离。注意本题可能会出现[1,5,2],[1,5,6].即1号城市到5号城市的距离为2,和1号城市到5号城市的距离为6.
3.解题思路
暴力解法:
1.先生成邻接表代表某个节点到某个节点距离为多少(这个需要取最小值因为题目的输入犯贱)
2.定义visit数组用来记录每个点是访问过还是没有访问过。
3.深度优先遍历从x节点开始遍历其所能到达的所有节点,从所有的可能性当中取一个距离最小的即可。
4.对应代码
int minDistance1(vector<vector<int>>& road, int n, int x, int y)
{
//注意城市的下标是从1位置开始的0位置丢弃不用
vector<vector<int>>Map(n + 1, vector<int>(n + 1, INT_MAX));
//一开始设计为整型最大代表不可达
for (int i = 0; i < n; i++)
{
//这是因为输入犯贱
//1 2 10
//1 2 9 有可能有这样的输入
Map[road[i][0]][road[i][1]] = min(Map[road[i][0]][road[i][1]], road[i][2]);
Map[road[i][1]][road[i][0]] = min(Map[road[i][1]][road[i][0]], road[i][2]);
}
//生成邻接表,Map[i][j]的含义代表 i到j的距离为d
vector<bool>visit(n+ 1);
return process(Map, x, y, visit, n);
}
//从cur这个节点到target这个节点的最小距离是多少
int process(vector<vector<int>>& Map, int cur, int target, vector<bool>& visit,int n)
{
//已经访问过了
if (visit[cur]) {
return INT_MAX;
}
if (cur == target) {//找到x这个节点了
return 0;
}
visit[cur] = true;
int ans = INT_MAX;
for (int next = 1; next <= n; next++)
{
//如果不是自己并且这个点可达并且没有访问过
if (next != cur && Map[cur][next] != INT_MAX && !visit[next]) {
int ret = process(Map, next, target, visit, n);//遍历其可达的节点
if (ret != INT_MAX) {//说明可以到达ret
ans = min(ans, ret+Map[cur][next]);
}
}
}
visit[cur] = false;
return ans;
}
但是这样的方式是最暴力的所有节点都搞一遍时间复杂都有点高。下面我们来看看迪结特斯拉算法怎么来解这个题
1.第一步和暴力解一样需要生成邻接表,并且需要求这个最小值这一步还是不变的
2.准备一个优先级对象小根堆和一个visit数组标记某个节点是否从堆中弹出过,如果已经在堆当中弹出过再次弹出的时候直接忽略调因为第一次弹出的距离是最小的。
3.一开始先将x这个节点加入到优先级队列当中加入的形式为Node类型,Node当中有这个路径和城市的编号。x到x的距离为0所有pathSum为0加入到优先级队列当中,进入队列当中后每次在弹出一个看是否来到y了,是直接返回路径和,不是开始遍历当前节点可达的城市并且没有访问过将其加入到队列当中。
下面我们来看看代码如何来实现
int minDistance2(vector<vector<int>>& road, int n, int x, int y)
{
vector<vector<int>>Map(n + 1, vector<int>(n + 1, INT_MAX));
//一开始设计为整型最大代表不可达
for (int i = 0; i < n; i++)
{
//这是因为输入犯贱
//1 2 10
//1 2 9 有可能有这样的输入
Map[road[i][0]][road[i][1]] = min(Map[road[i][0]][road[i][1]], road[i][2]);
Map[road[i][1]][road[i][0]] = min(Map[road[i][1]][road[i][0]], road[i][2]);
}
vector<bool>visit(n + 1);
auto cmp = [&](Node& a, Node& b) {return a.pathSum > b.pathSum; };
priority_queue <Node, vector<Node>, decltype(cmp)>minHeap(cmp);
//小根堆
minHeap.push(Node(x,0));//x到x的距离为0
while (!minHeap.empty())
{
auto node = minHeap.top();
minHeap.pop();
//已经弹出过的节点不在弹出
if (visit[node.city] == true) {
continue;
}
if (node.city == y) {
return node.pathSum;
}
visit[node.city] = true;//当前这个节点已经被访问过了
for (int next = 1; next <= n; next++)
{
if (next != node.city && !visit[next] && Map[node.city][next] != INT_MAX) {
minHeap.push(Node(next,node.pathSum + Map[node.city][next]));
}
}
}
return INT_MAX;//x到y不可达
}
对应总代码包含测试代码
#include下面我们还可以看看牛客网上的一道题来验证这道题的正确性
1.对应牛客网链接
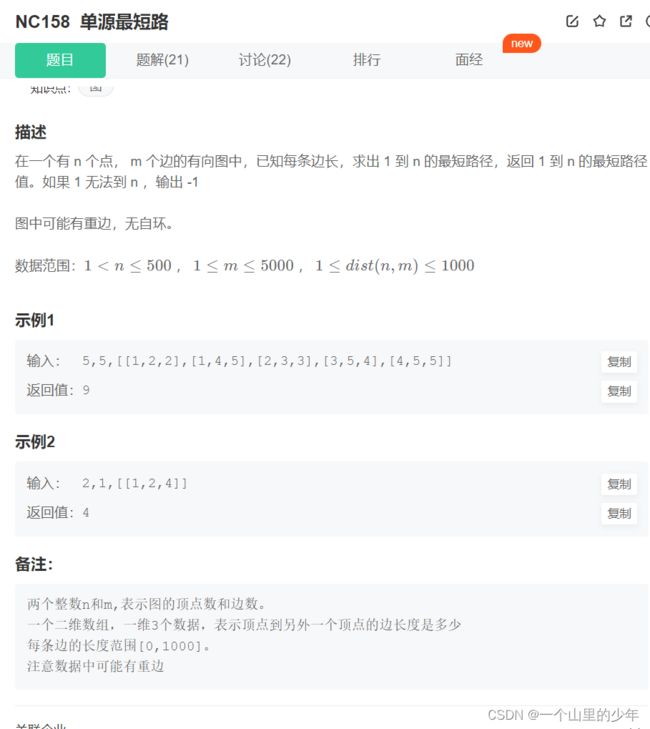
单源最短路径
2.题目描述
3.解题思路
这个题其实就是上面那个题的弱化版本,这里变成了有效图只要拿上面那个代码给一下下就可以了,非常的简单在这里就只给出代码不做过多解释了。
4.对应代码
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param n int 顶点数
* @param m int 边数
* @param graph intvector> 一维3个数据,表示顶点到另外一个顶点的边长度是多少
* @return int
*/
struct Node
{
Node(int c,int p)
:pathSum(p),city(c)
{}
int pathSum;
int city;
};
int findShortestPath(int n, int m, vector<vector<int> >& graph) {
// write code here
vector<vector<int>>Map(n+1,vector<int>(n+1,INT_MAX));
for(auto&road:graph)
{
Map[road[0]][road[1]]=min(Map[road[0]][road[1]],road[2]);
}
vector<bool>visit(n+1);
auto cmp=[&](Node&a,Node&b){return a.pathSum>b.pathSum;};
priority_queue<Node,vector<Node>,decltype(cmp)>minHeap(cmp);
minHeap.push(Node(1,0));
while(!minHeap.empty())
{
auto node=minHeap.top();
minHeap.pop();
if(visit[node.city]){
continue;
}
visit[node.city]=true;
if(node.city==n){
return node.pathSum;
}
for(int i=1;i<=n;i++){
if(i!=node.city&&Map[node.city][i]!=INT_MAX&&!visit[i]){
minHeap.push(Node(i,node.pathSum+Map[node.city][i]));
}
}
}
return -1;
}
};
4键键盘
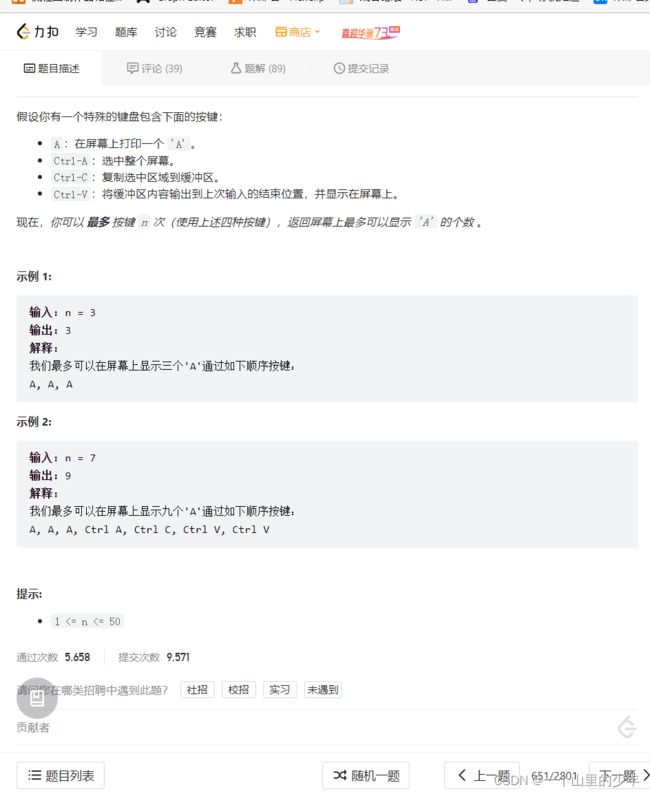
1.对应letecode链接:
https://leetcode.cn/problems/4-keys-keyboard/
2.题目描述
3.解题思路
1.首先我们可以确定 6步以内我们只打A是最优秀的。如果有老铁不认可可以下来看看,6步以内打A就是最经济的选择
2.最优解一定不是连续粘贴5次得到的,一定是粘贴一次,粘贴两次,粘贴三次,粘贴四次得到的。粘贴五次得不到最有解。下面我们举个列子就知道了。
假设我们第12步屏幕上有S个A,此时第13步选择全选,第14步选择复制,第15步选择粘贴,第16步选择粘贴,第17步选择粘贴,第18步选择粘贴,第19步选择粘贴。此时屏幕上有6S个A,而粘贴办版上有S个A。下面我们在来看看这种方式下就比这种可能性要更优
同样的我们假设第12步的时候一共有S个A,我们第13步选择全选,第14步选择复制,第15步选择粘贴,第16步选择全选,第17步选择复制,第18步选择粘贴,第19步也选择粘贴。此时我们得到屏幕上A的数量也是6S个但是粘贴版上A的数量有2S个比上面的那种方法要更优秀。
假设我们定义dp[i]为i+1以内(下标变换而已)最多能有多少个A,那么可能性只有可能是4次粘贴里面最大的那个。如果是一次粘贴那么i-2步一定是全选,i-1步一定是复制,所有dp[i]=2dp[i-3].粘贴两次也是同理在这里即步推导了
4.对应代码
class Solution {
public:
int maxA(int n) {
vector<int>dp(n);
for(int i=0;i<6&&i<n;i++){
dp[i]=i+1;//下标变换而已
}
// 可以证明:
// 来到i的时候,包括i在内最多有连续4次粘贴行为
// 不可能更多,如果有连续5次粘贴,一定就不再是最优解
// 假设开始时,A的数量为S,看如下的变化过程,我们称这是行为一:
// 开始 全选 复制(粘贴板S个A) 粘贴 粘贴 粘贴 粘贴 粘贴
// S S S 2*S 3*S 4*S 5*S 6*S
// 但是,注意看如下的行为二:
// 开始 全选 复制(粘贴板S个A) 粘贴 全选 复制(粘贴板2S个A) 粘贴 粘贴
// S S S 2*S 2*S 2*S 4*S 6*S
// 行为一,经历8步,最后是6*S个A
// 行为二,经历8步,最后是6*S个A
// 但是行为二在粘贴板上有2S个A,而行为一在粘贴板上有S个A
// 所以行为一没有行为二优
// 以此说明:来到i的时候,包括i在内最多有连续4次粘贴行为
// 那么就尝试:连续1次、连续2次、连续3次、连续4次粘贴行为即可
for(int i=6;i<n;i++)
{
dp[i]=max(max(dp[i-3]*2,dp[i-4]*3),max(dp[i-5]*4,dp[i-6]*5));
}
return dp[n-1];
}
};
冗余的边II
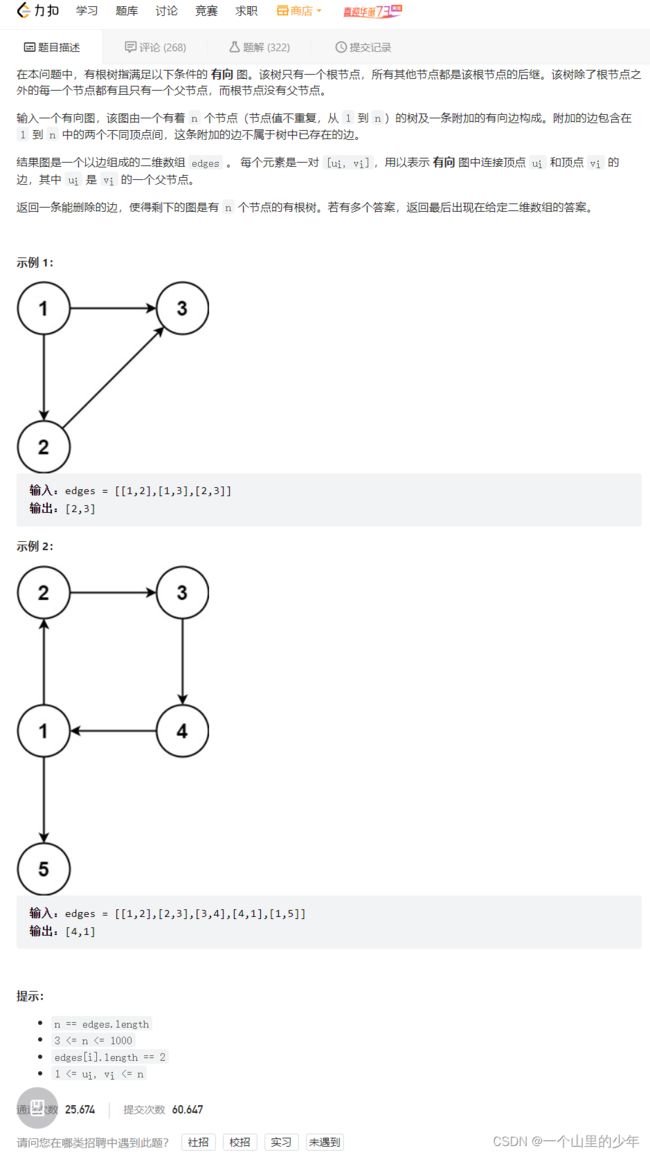
1.对应letecode链接:
冗余的边
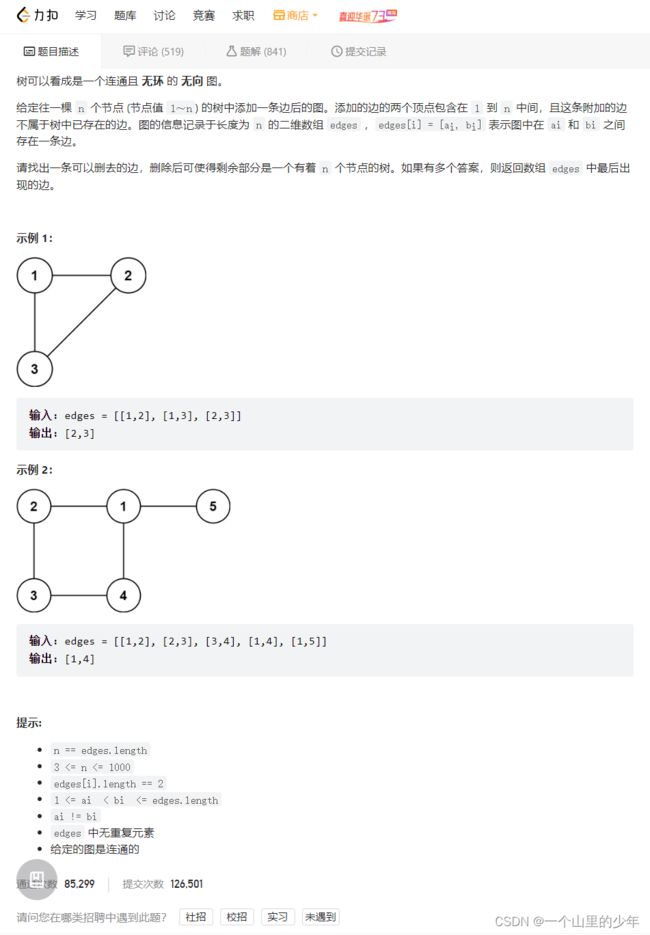
2.题目描述
3.解题思路
1.如果整个树上没有入度为2的点那么让这颗树形成环的那条边就是冗余的边
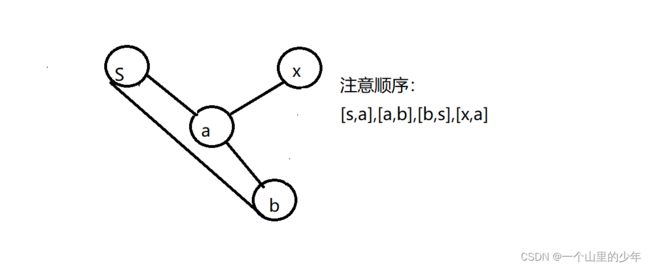
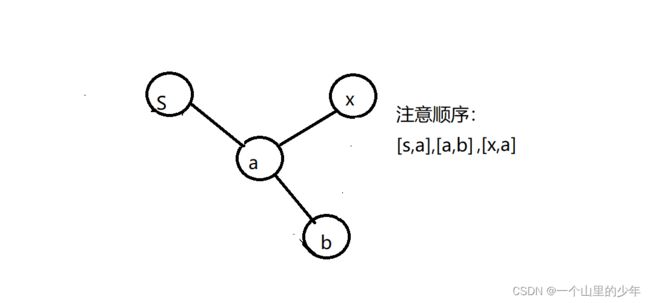
2.如果有入度为2的边那么情况就比较复杂了,下面我们来进行分析一下。给出下面几种情况
此时我们需要删除一条边是x到a,大致思路是我们需要一个并查集来帮助我们来判断是否能够形成环,但是在合并的过程当中一个节点只有第一次来到我们才将其放到并查集当中进行合并,下面我们以上面这个列子为例,从s到出发一直合并到x点,此时x点有一条边到a但是此时我们不合并,那么此时我们没有检测到有环,在记录的过程当中我们需要记录一下是那两个点到的这个点,第一个点记为first,第二个点记为second就如这种情况本来是有环的但是我们实际上没有检测到环,此时冗余的边一定是second
下面我们在来看另外一种情况:
此时在这种情况下我们从s节点出发使用并查集一直合并到b这个节点的时候我们发现环了,出现[x,a]这条边的时候a的入度变为了2此时一定是s到a这条边有问题也就是第一次到a的这条边是冗余的边。
下面我们来看看最后一种情况:
这种情况下我们直接按照题目的意思返回最后一个即可,即第二次到这个节点那条边。也就是second
4.对应代码
class Solution {
public:
class UniFind {
public:
UniFind(int n) {
parent.resize(n + 1);
size.resize(n + 1);
help.resize(n + 1);
for (int i = 1; i <= n; i++) {
parent[i] = i;
size[i] = i;
}
}
int findFather(int i) {
int hi = 0;
while (parent[i] != i) {
i = parent[i];
help[hi++] = i;
}
hi--;
while (hi >= 0) {
parent[help[hi--]] = i;
}
return i;
}
bool IsSame(int i, int j) {
return findFather(i) == findFather(j);
}
void Union(int i, int j) {
int fatheri = findFather(i);
int fatherj = findFather(j);
if (fatheri != fatherj) {
if (size[fatheri] >= size[fatherj]) {
size[fatheri] += size[fatherj];
parent[fatherj] = fatheri;
} else {
size[fatherj] += size[fatheri];
parent[fatheri] = fatherj;
}
}
}
private:
vector<int>parent;
vector<int>size;
vector<int>help;
};
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int N = edges.size();
vector<int>prev(N + 1);
UniFind uf(N);
/*
prev[i]=0代表的是i这个节点第一次来到
prev[i]不为0代表是第二次来到了其值代表是那个节点来到我的
*/
vector<int>first;
vector<int>second;
vector<int>circle;//含义有点复杂
// 如果,没有入度为2的点,
// first second 都维持是null
// 如果,有入度为2的点,那么也只可能有一个
// 比如入度为2的点,是5
// first = [3,5]
// second = [12,5]
for (int i = 0; i < N; i++) {
int from = edges[i][0];
int to = edges[i][1];
if (prev[to] != 0) { //不是第一次到这个点了
//分别记录是第一次到这个点和第二次到这个点
first = {prev[to], to};
second = edges[i];
} else {
//to这个点是第一次来的
prev[to] = from;
if (uf.IsSame(from, to)) {//看是否形成环了
circle = edges[i];
} else {
uf.Union(from, to);//进行合并
}
}
}
//如果first为空那么second也一定为空
return first.empty() ? circle : (circle.empty() ? second : first);
}
};
下面我们在看来看看一到弱化版本的题目
冗余的边
1.对应letecode链接
https://leetcode.cn/problems/redundant-connection/
2.题目描述
3.解题思路
本题相对于上面那个题目而言比较容易,只需要一个并查集来进行边的合并之只要检测到了有环那么那个导致成环的那条边就是冗余的边
4.对应代码
class Solution {
public:
struct UnFind
{
UnFind(int n)
{
parent.resize(n+1);
size.resize(n+1);
help.resize(n+1);
for(int i=1;i<=n;i++){
parent[i]=i;
size[i]=1;
}
}
int findFather(int i)
{
int hi=0;
while(i!=parent[i])
{
i=parent[i];
help[hi++]=i;
}
hi--;
while(hi>=0)
{
parent[help[hi--]]=i;
}
return i;
}
bool IsSame(int i,int j)
{
return findFather(i)==findFather(j);
}
void Union(int i,int j)
{
int findi=findFather(i);
int findj=findFather(j);
if(findi!=findj)
{
if(size[findi]>=size[findj])
{
size[findi]+=size[findj];
parent[findj]=findi;
}
else
{
size[findj]+=size[findi];
parent[findi]=findj;
}
}
}
vector<int>parent;
vector<int>size;
vector<int>help;
};
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n=edges.size();
UnFind uf(n);
//无相图只要找到环肯定就是那条冗余的边
for(auto &edge:edges)
{
int from=edge[0];
int to=edge[1];
if(uf.IsSame(from,to)){
return edge;
}
else
{
uf.Union(from,to);
}
}
return {};
}
};