HDLCoder的系统设计

HDL Coder 的系统设计

在当前算法更新迭代较快的时代，采用传统编写HDL实现算法的方式给设计带来较大的挑战，往往算法上较小的调整在HDL上需要大量的工作与仿真才能完成。Matlab通过HDL Coder生成 HDL 代码并将该代码部署在专用集成电路 (ASIC) 或现场可编程门阵列 (FPGA) 上，在硬件中实现 MATLAB 算法。使用与 HDL 代码生成兼容的语法和函数编写 MATLAB 算法。
在算法中使用浮点数据时，HDL Coder中的Fix Point conversion将其转换为定点。定点化后生成 HDL 代码，进行速度和面积优化后并验证它与原始算法匹配。本文从Fix Point conversion、Code generation、Speed and Area Optimization三个方面对其进行阐述。

Fix Point conversion

在数字硬件中，数字以二进制字存储，而二进制字是固定长度的位序列，由1 和 0 来表达。二进制数表示为定点或浮点数据类型。

定点数据类型

定点数据类型的特征在于以位为单位的字长、二进制小数点的位置以及它是有符号还是无符号。二进制小数点的位置的移动是缩放和改变定点值的有效方法。
例如，广义定点数（有符号或无符号）的二进制表示如下所示：

图1定点数二进制表示
最高位b_(wl-1)是符号位，决定定点数是否正负。b_(wl-2)至b_4为整数部分，二进制小数点显示在b_4和b_3之间，剩下b_3至b_0表示小数位。在此示例中，该数字被称为具有四个小数位，或小数长度为 4。定点数据类型可以是有符号的或无符号的。定点值是有符号还是无符号通常不会在二进制字中显式编码；也就是说，没有符号位。相反，符号信息是在计算机体系结构中隐式定义的。
现举例说明定点数转实数，现有8位定点数，其中整数位有4位，小数位有4位，计算其结果。具体计算定点数转实数步骤下所示。
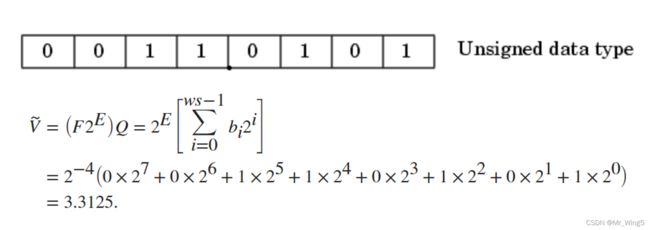图2定点数转实数

浮点数据类型

定点数的局限性在于它们不能使用合理的字长同时表示非常大或非常小的数字。这个限制可以通过使用科学记数法来克服。使用浮点计数数法，可以动态地将二进制小数点放置在方便的位置，并使用二进制数的幂来跟踪该位置。因此，可以仅用几位数字表示一系列非常大和非常小的数字。
任何二进制浮点数以科学记数法形式表示为f2e，其中f是分数（或尾数）， 2是基数或底数（在本例中为二进制），e 是基数的指数。基数总是正数，而 f和e可以是正数或负数。在执行算术运算时，浮点硬件必须考虑到符号、指数和分数都编码在同一个二进制字中。与用于二进制定点运算的电路相比，这会导致复杂的逻辑电路。以下举例说明双精度浮点数。
IEEE 双精度浮点格式是一个 64 位字，分为 1 位符号指示符s、11 位偏置指数e和 52 位小数f。
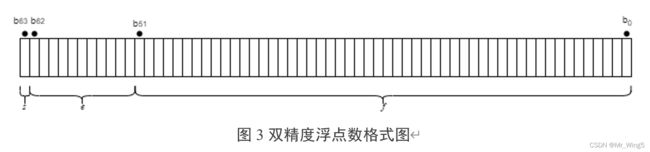图3双精度浮点数格式图
双精度格式与实数表示之间的关系由下式给出
图4双精度格式与实数关系式
其他的浮点数类型在这里不再过多解释，以下列出常用3中浮点数类型的范围、偏差和精度。

Data Type	Low Limit	High Limit	Exponent Bias	Precision
Half	2(-14) = 6.1*10-5	(2-2-10 )215 = 6.5104	15	2-10 = 10-3
Single	2(-126) = 10-38	2128 = 3*1038	127	2-23 = 10-7
Double	2(-1022) = 2*10-308	21024 = 2*10308	1023	2-52 = 10-16

表5常见3中种浮点数范围、偏差、精度

硬件为什么需要定点化

数字硬件正在成为实现控制系统和信号处理滤波器的主要手段。数字硬件可分为现成硬件（如微控制器、微处理器、通用处理器和数字信号处理器）或自定义硬件。在这两种类型的硬件中，有许多架构设计。这些设计涵盖了从单指令单数据流处理单元的系统到多指令多数据流处理单元的系统。
在数字硬件中，数字以定点或浮点数据类型的形式来表示。对于这两种数据类型，字长的位数都是固定的。但是，定点值的动态范围远小于字长相同的浮点值。既然浮点处理器可以大大简化控制规则或数字滤波器的实时实现，并且浮点数可以有效逼近实际数字，那么为什么还要使用具有定点硬件支持的微控制器或处理器？因此，为避免溢出或不合理的量化误差，必须对定点值进行定标。
1.大小和功耗：与浮点硬件相比，定点硬件的逻辑电路的复杂性要低得多。这意味着与浮点硬件相比，定点芯片的大小更小、功耗更低。以一款移动电话为例，它的一个产品设计目标是移动性尽可能高（小巧轻便）。如果使用现今的高端浮点通用处理器，则还需要大型散热器和电池，从而导致移动电话成本高昂、体积庞大而且很重。
2.内存使用和速度：通常，执行定点计算需要更少的内存和更少的处理器时间。
3.成本：在性价比是一项重要考虑因素的情况下，定点硬件更具成本效益。在产品（尤其是批量生产的产品）中使用数字硬件时，定点硬件的成本远低于浮点硬件，从而可以显著节省成本。在决定使用定点硬件后，下一步是选择一种实现动态系统的方法（例如控制系统或数字滤波器）。由于时间或内存大小的限制，通常会排除浮点软件仿真库。因此，在对二元整数值进行定标时只能选用定点数学。

Fixed-Point Conversion

Fixed-Point Conversion提供用于在嵌入式硬件上优化和实现定点和浮点算法的数据类型和工具。其中包括定点和浮点数据类型以及特定于目标的数值设置。使用 Fixed-Point Conversion，可以执行定点位真的目标感知仿真。然后，在硬件上实现设计之前，可以测试和调试量化效应，如溢出和精度损失。并且可以用于分析双精度算法并将它们转换为精度降低的浮点或定点。优化工具使能够选择满足数值精度要求和目标硬件约束的数据类型。为了高效实现，可以用硬件最优模式（如压缩查找表）来代替计算成本高昂的设计构造。
打开Fixed-Point Conversion ，添加浮点滤波器算法文件
图6 Fixed-Point Conversion初始界面图
添加测试文件确定输入输出接口
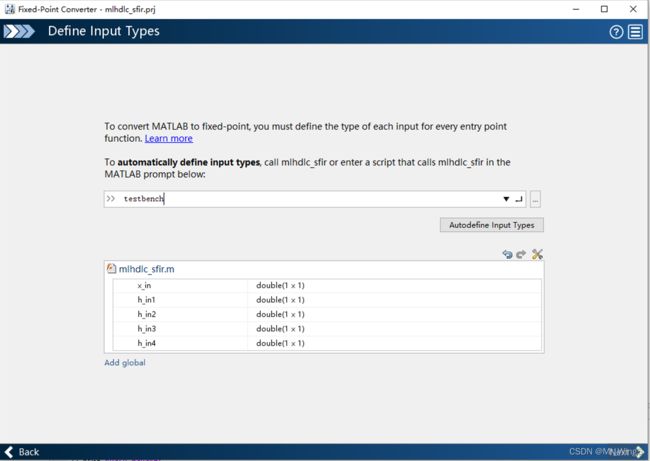图7 输入输出图
进行数值分析，得出类型与范围、定点化规则。
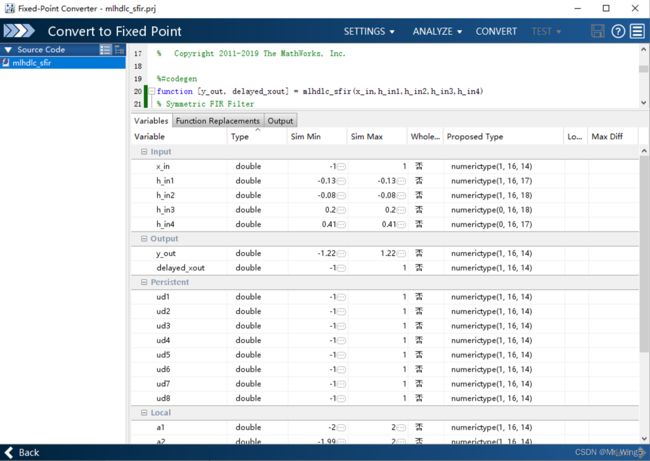图8 数值动态分析
将算法定点化
图9 算法定点化
生成算法和原算法对比
图10 FIR滤波器原算法
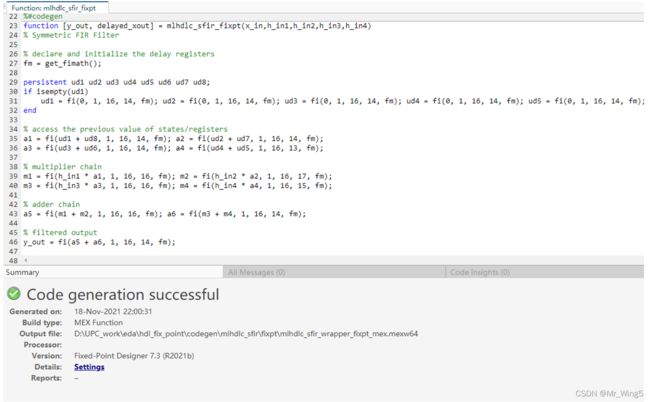图11 FIR滤波器定点化算法
数据测试与误差分析：
图12 原算法输出和定点化算法输出误差分析图
在Simulink中可以分析数据定点化后是否上下溢出，在设计时可以依据此来改变定点数格式。
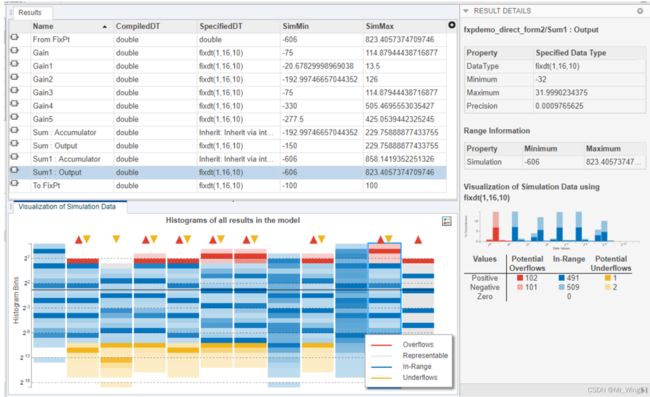图13 数据动态分析溢出情况
可以看出SUM1：Output输出脚在激励情况下不同时间数据溢出情况。

Code generation

在MATLAB中HDL的生成现目前集成为HDL Workflow Advisor。同时也包括定点化，所以我们可以选择在HDL Workflow Advisor或Fixed-Point Conversion定点化算法。该APP提供了各种工作流来检查算法的 HDL 兼容性、生成 HDL 代码、验证代码，然后将代码部署到目标FPGA平台。现在我们继续设计上面的定点化后的FIR滤波器。打开HDL Coder，加载源文件和激励代码
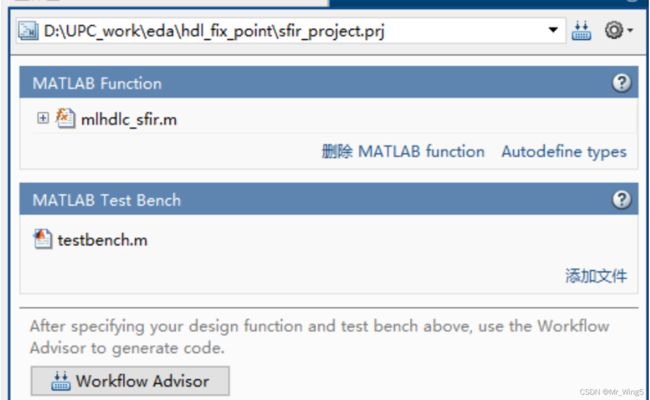图14 HDL Coder生成图
HDL Workflow Advisor初始界面如下所示
图15 HDL Workflow Advisor初始界面图
界面中包括定义输出、定点化、选择代码标签、代码生成。
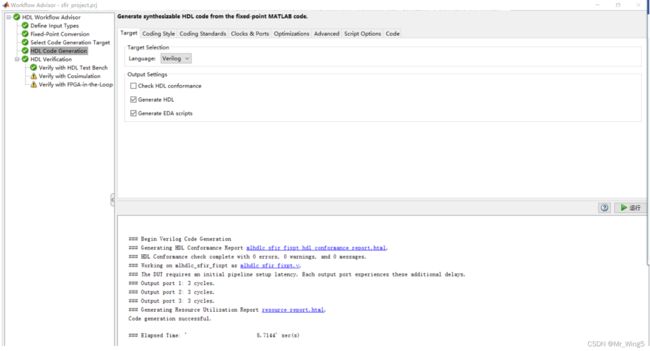图16 HDL Code Generation参数设置
在HDL Code Generation 中我们可以设置大量的参数例如生成代码为Verilog还是VHDL，生成各种文件的后缀标识，RLT代码标准如长度、深度、位宽等，时钟复位同步和有效，以及速度和面积优化，以及输出Modelsim仿真do文件和Xilinx Vivado的TCL脚本文件。如下所示：
图17 输出参数设置
生成文件如下图所示
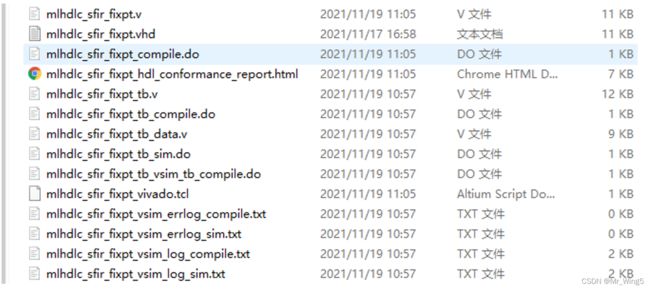图18 HDL Code Generation 生成代码文件列表
打开Modelsim后执行do脚本语言，进行仿真结果如下
图19 Modelsim仿真图
参考MATLAB生成的仿真图如下所示
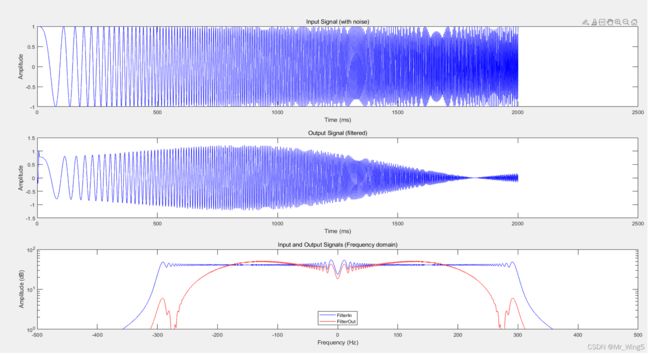图20 MATLAB仿真图
可以对比出，在MATAB中仿真的浮点算法和在Modelsim中仿真的定点算法几乎没有区别。然后打开vivado后运行Tcl脚本语言
图21 Vivado TCL脚本加载图
自动完成综合布线
图22 Vivado 自动完成综合布线
MATLAB生成的资源使用情况
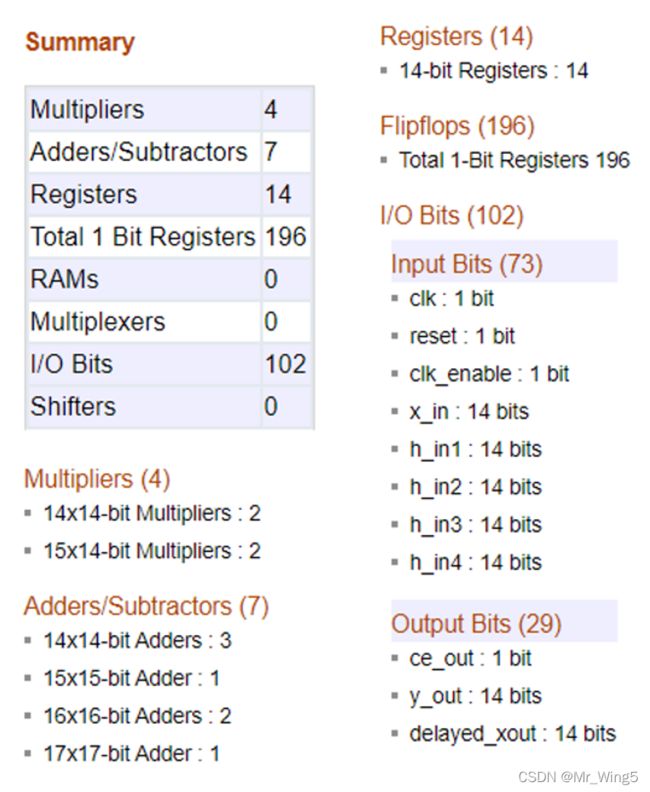图23 MATLAB仿真资源使用情况

Speed and Area Optimization

在 HDL Coder中使用面积和速度优化来节省资源并改进目标 FPGA 设备上的设计时序。优化不会改变算法的功能行为，但可以优化设计中的某些资源、引入延迟或导致采样率差异。可以生成最初 HDL 代码并在 FPGA 平台上综合设计，而无需启用优化。如果设计不满足时序要求，可以启用优化并重新运行工作流程，直到设计满足面积和速度要求。
MATLAB 打开 Workflow Advisor。在 Advisor 的HDL Code Generation 任务中，启用Optimization选项卡中的设置。
图24 Workflow Advisor Optimization选项
各种优化在不同层次的情况

Optimization	Model Level	Subsystem Level
Delay balancing	Yes	Yes
RAM mapping	Yes	No
Adaptive pipelining	Yes	Yes
Clock rate pipelining	Yes	Yes
Distributed pipelining	Yes	Yes
Resource sharing	Yes	Yes
Streaming	No	Yes

图25 不同优化情况

速度优化

分布式流水线是 HDL Coder 支持的子系统范围优化，用于实现高时钟速度硬件。通过开启’Distributed Pipelining’，编码器将子系统的输入流水线寄存器、输出流水线寄存器和子系统中的寄存器重新分配到适当的位置，以最大限度地减少寄存器之间的组合逻辑，并最大限度地提高从生成的芯片合成的时钟速度HDL 代码。
考虑以下对称 FIR 滤波器的示例模型。从输入或寄存器到输出或另一个寄存器的组合逻辑包含一个乘积块和一个加法器树。分布式流水线将移动在子系统级别设置的输出寄存器，以降低组合逻辑的级别。
图26 FIR滤波器模型
分布式流水线是子系统模块选项之一。一旦开启，子系统中的寄存器，包括输出流水线寄存器和输入流水线寄存器，将重新定位以实现最佳时钟速度。它相当于在子系统级别重新定时。代码生成模型明确反映了子系统中的分布式寄存器（以橙色突出显示）。
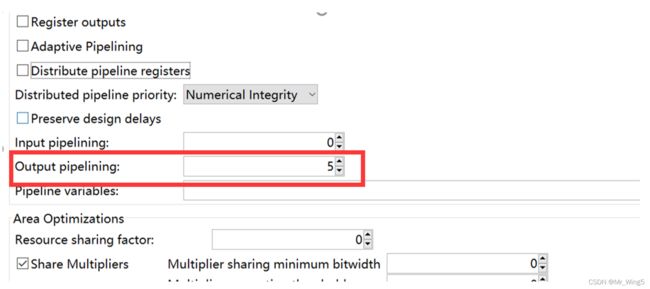图27 输出流水选择
图28 FIR滤波器输出流水优化后结构图
由于“分布式流水线”是子系统级参数，层次结构中不同级别的不同子系统可以指定不同的流水线阶段值和不同的“分布式流水线”设置。默认情况下，编码器仅在该子系统中分配指定子系统的寄存器，而不是通过较低级别的子系统。如果需要跨层级分布，用户可以将较低子系统的“分布式流水线”设置为“开”，然后打开全局选项“层级分布式流水线”。当 local 和 global 选项打开时，整个子系统，包括较低级别的子系统，在分配寄存器时将被视为单个子系统。

面积优化

由于时分复用架构需要更长的延迟才能完成操作，HDL Coder会根据共享的资源自动管理时序差异。假设共享资源以基本采样率运行，那么资源共享被实现为本地多速率架构，如本例所述。如果共享资源以比基本采样率更慢的采样率运行，则 HDL Coder会调用时钟速率流水线来综合利用速率差异中定义的延迟预算的实现。在这种情况下，资源共享架构是单速率实现，需要多个时间步骤来完成所有共享操作。该单率的资源共享体系结构 描述了这个实现的细节。
上诉滤波器例子中抽象出来结构如下所示，输入多级延迟后与4个加法器计算后，再送给4个乘法器，最后再有加法器输出。

图29 FIR滤波器抽象资源图
要减少区域资源，可以通过将子系统上的SharingFactor参数设置为正整数值来调用共享优化。在此示例中，有 4个乘法器，因此生成 HDL 时将SharingFactor设置为 4 生成具有 1个乘法器的 HDL。
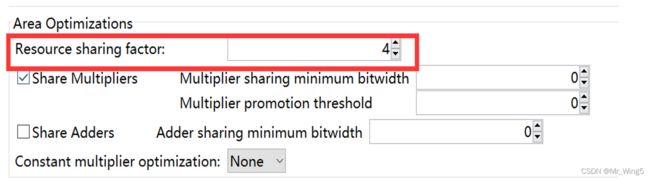图30 资源复用优化
代码生成模型反映了共享架构。可以看见4个乘法器变为1个乘法器加2个数据选择器，这样实现面积的优化。
图31 FIR滤波器输出优化后抽象框图

延迟平衡

HDL Coder支持将离散延迟引入模型的多种优化、模块实现和选项，目的是提高硬件使用效率或实现更高的时钟速率。输出流水线、流媒体或资源共享等优化可能会引入延迟。一些块实现，例如 Newton-Raphson 和 CORDIC 架构，在生成的代码中引入了延迟。
当优化或模块实现选项沿模型中的关键路径引入延迟时，原始模型和生成的模型或 HDL 代码的数值可能不同，因为等效延迟不会在其他并行信号路径上引入。沿着其他路径手动插入补偿延迟是可能的，但容易出错，并且不能很好地扩展到具有许多信号路径或多个采样率的大型模型。
为了避免这个问题，HDL Coder 支持延迟平衡。默认情况下，模型上启用延迟平衡。代码生成器检测沿一条路径引入的新延迟，然后在其他路径上插入匹配的延迟。启用延迟平衡时，生成的模型在功能上等同于原始模型。
MATLAB中的一些算术块需要复杂的硬件算法。例如，考虑倒数平方根块。此模块中的单个时间步中计算其答案。如果相应的硬件实现应与MATLAB 保持周期精确，则该模块的硬件算法必须在单个时钟周期内计算。然而，这会导致很长的关键路径，从而降低硬件的时钟频率和效率。因此，HDL Coder 以 5 周期延迟实现此模块，这意味着包含此模块的每条路径都会引入 5 周期延迟。
举个例子，其中包含一个实现“Sqrt”函数的平方根块，将会占用2个时钟周期，于是可以设置并行路径的“Gain3”块的“OutputPipeline”实现参数设置为 2。得到如下图所示。
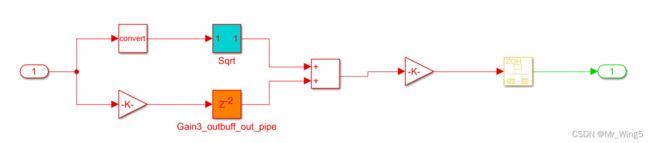图32 Sqrt相加系统结构图
由于在convert阶段占用1个时钟周期了，会导致并行的两路数据到达时间不同，产生了延迟。为了解决功能等价问题，用户可以通过将模型级别的“BalanceDelays”选项设置为“on”来打开延迟平衡功能。启用此选项后，HDL Coder 将自动识别需要添加匹配延迟以保证功能等效的位置。
图33 Sqrt相加系统延迟优化结构图
可以看出，平衡延迟后MALTAB自动在并行路中插了一级流水，这会使得并行两路数据到达时间相同。
延迟图如下所示
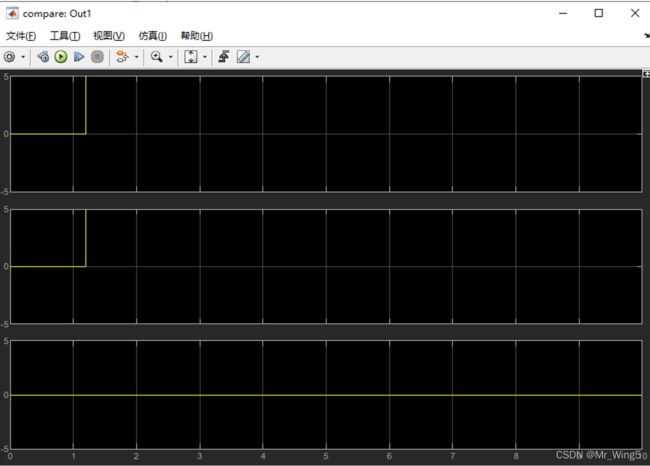图34 系统延迟对比图